基于邻近度的安徽省人均GDP组合预测模型*

李燕飞， 吴 涛,2**， 郭海艳

(1.安徽大学 数学科学学院，合肥230601；2.安徽大学 计算机智能与信号处理教育部重点实验室，合肥230039)

0 引 言

尽管目前中国经济下行压力有所加大，部分企业经营困难较多，长期积累的风险隐患有所暴露，但习近平主席明确表示，对中国经济发展前景，大家完全可以抱着乐观态度。安徽省作为中部大省，对安徽未来几年人均GDP合理预测可窥得中国经济发展一斑。单一的预测方法得到的结果不够准确，而将预测结果加权组合则会得到更好的预测结果。Bates J M和Granger C W J[1]在1969年首次提出了组合的概念，而后国内外许多学者开始研究组合预测模型。唐小我[2]用组合预测误差平方和极小化来确定最优加权系数，并导出了简单平均预测是最优组合预测的条件。陈华友[3]基于预测方法有效度的概念，建立了改进的组合预测模型，并给出其线性规划的解法。谢开贵等[4]给出了基于最小二乘和最小一乘准则的线性回归组合预测模型, 然后应用最小二乘原理得到权系数最小二乘估计值。

介绍了组合预测邻近度的概念并证明了邻近度的相关性质，随后引入了一种新的组合权系数求解方法MEM算法[5-6]建立了基于邻近度的组合预测模型。组合预测的关键问题是求出各单项预测加权平均系数，普通的组合预测模型是以误差平方和离差绝对值最小为准则建立起来的，然而这些组合预测模型对于不遵循大多数样本所显示的相同关系的离群值不具有鲁棒性，且在不对称分布情况下，由于限制了权系数和为1，因此在各单项预测的结果一致偏大或偏小时，难以得到精确的预测结果。而提出的组合预测邻近度概念和引入的众数极大期望解法有效地克服了这些缺点。由最后的实例分析可以看出方法的可行性和有效性。

1 基于邻近度的加权几何平均组合预测模型的建立

1.1 邻近度的概念

设某一预测问题的指标序列是xt,t=1,2,…,N。对于这个预测问题，有m种单项预测方法对其进行预测，设xit为第i种单项预测模型在第t时刻的预测值，i=1,2,…,m。设li为第i种单项预测方法的加权系数，li≥0,i=1,2,…,m。加权几何平均组合预测是常用的组合预测方法之一，它通常比加权算术平均组合预测方法有更小的相对误差。根据加权几何平均计算公式,令

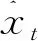
设组合预测误差为εt，则有

定义1 (邻近度)令

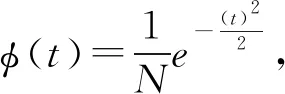
性质1Q随|εt|减小而增大，随εt增大而减小。

证明|εt1|≤|εt2|⟹(εt1)2≤(εt2)2，所以φ(εt1)≤φ(εt2)，其他时刻误差不变，有Q1≤Q2，因此性质1成立。

性质2 ∀t∈{1,2,…,N}，εt=0时，即各时刻组合预测值都等于实际值时，邻近度Q最大，且邻近度等于1。

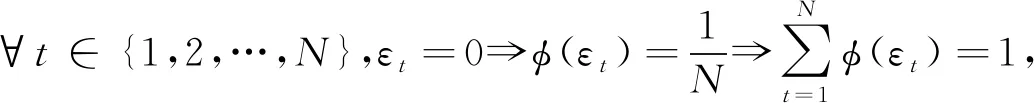
性质3 基于邻近度组合预测模型对于存在不遵循大多数样本所显示的相同关系的离群值较基于误差平方和最小或离差绝对值最小模型更具有鲁棒性。

1.2 基于邻近度的组合预测模型建立

基于邻近度组合预测邻近度越大，表示预测越精确。模型的关键是求最大化Q值时的组合权系数。令αt=(lnx1t,lnx2t,…,lnxmt)T,γt=lnxt,t=1,2,…,N.问题则转化为了一个回归问题

γt=βTαt+εt

其中β是一个m维列向量，β=(l1,l2,…,lm)，使用文献[6]给出的众数极大化期望MEM算法以在最大化Q的情况下求出各单项预测方法组合权重向量β。先给一个初始的β(0)，则它的k+1步公式为

E步：

M步：

(αTWkα)-1αTWkγ，其中α=(α1,α2,…,αN)T，Wk是一个n×n对角矩阵，Wk=diag{π(1|β(k)),π(2|β(k)),…,π(N|β(k))},γ=(γ1,γ2,…,γN)T.多次迭代以后MEM 算法使得参数β收敛到一个局部最优解，因此需要多次对起始点进行选择，以期望得出全局最优解，这时迭代出的参数β就是要求的各单项预测组合权重向量。

1.3 模型有效性评价准则

使用以下4个模型常用的评价准则对各模型效果进行评价。

误差平方和：

(1)

平均绝对误差：

(2)

平均绝对百分比误差：

(3)

均方百分比误差：

(4)

2 实例分析

选取2000—2017年安徽省人均GDP为研究训练样本，数据自国家统计局网站，分别使用指数预测、抛物线预测和移动平均预测等3种单项预测方法对安徽省人均GDP进行预测。

2.1 单项预测模型

2.1.1 指数预测模型

从图1(a)的趋势图可以看出，安徽省人均GDP有明显的随时序增长的趋势，并大致随时间呈指数增长，因此可选用指数预测模型，拟合方程为

lnx1t=8.278 1+0.142 2×t

利用模型对安徽省人均GDP进行预测，预测值及精度如表1所示。

2.1.2 抛物线预测模型

从图1(b)可以看出，由抛物线预测得到的人均GDP随年份增长曲线与真实增长曲线相和度也很高，其拟合方程为

x2t=3.317 0+0.410 5×t+0.105 4×t2

t代表年份，从1开始对应着2000年。运用模型对安徽省人均GDP进行预测预测值及精度如表1所示。

2.1.3 移动平均预测模型

移动平均预测是由移动平均法根据时间序列，逐项推移，依次计算包含一定项数时序的平均数，并以此进行预测的方法。这里取移动平均项数等于2，移动平均序列预测趋势与真实值曲线对比如图1(c),其拟合方程为

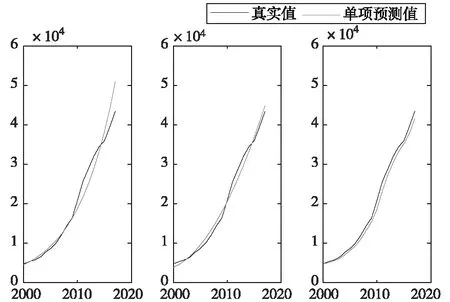
(a) 指数预测 (b) 抛物线预测 (c) 移动平均预测

预测方程为x3t+T=at+bt×T，其中at,bt为待估参数，T为步长。使用模型对安徽省人均GDP进行预测预测值及精度如表1所示。

分析表1可知:3种单项预测均能正确反应人均GDP变化趋势，抛物线预测模型与移动平均预测模型在各时刻预测精度趋于平稳，而指数预测则在后期精度越来越低，总的来讲3个单项预测精度都不够高。不能达到准确预测的要求，因此需要对其进行组合以得到精度更高的预测数值。

2.2 组合预测模型

由表1种各单项预测值为基础，建立基于邻近度的组合预测模型，用matlab求解得最优权系数向量βT=(-0.171 5,0.238 9,0.938 4)，以该权重代回加权组合预测模型得到计算结果如表2所示。从预测值精度可以看出，组合预测精度大部分达到99%以上，最低的也超过了96%，预测结果明显优于3项单项预测值精度。且基于邻近度的组合预测在各个时刻预测精度不仅高而且稳定，因此在预测未来时序中人均GDP数值时预测结果更为可靠。

由于各种单项预测方法都是基于往期数据进行建模预测，故建模时所利用数据在长期预测时不具有时效性，所以预测方法对于短期预测更加精准。

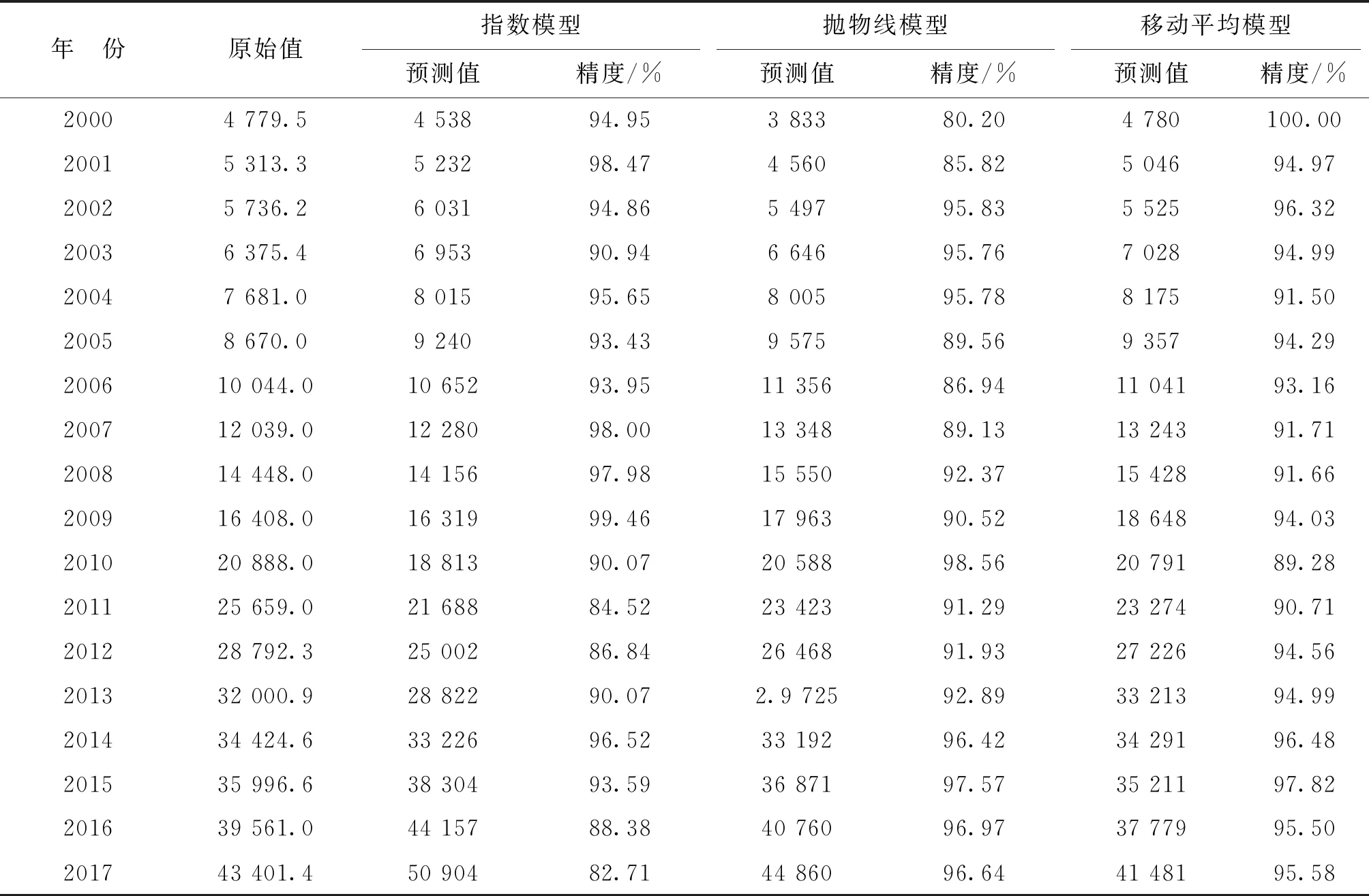
表 1 各单项预测模型预测值与预测精度

表 2 基于邻近度的组合预测预测值及预测精度

选择误差平方和(SSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和均方百分比误差(MSPE)这4项评价准则，结合式(1)、式(2)、式(3)、式(4)对3种单项预测模型及提出的组合预测模型和文献[9]提出的组合预测模型预测效果进行比较，5种模型预测误差如表3所示。

表 3 模型误差评价

从表3可以看出基于邻近度的组合预测模型在4个评价准则上效果均显著优于单项预测模型及文献[9]提出的组合预测模型。说明模型的合理性。

在训练集上拥有很好的预测效果并不足以说明模型预测效果的稳定性和在未来时间上预测结果的有效性，因此需要引入测试集来观察模型在未来时间上预测效果。各模型在测试集上预测效果见表4。

2.3 安徽省人均GDP预测

由表1、表2、表3、表4对比发现，相较于单项预测方法，基于邻近度的组合预测显著提高了预测精度，因此利用基于邻近度的组合预测模型对2019—2021年安徽省人均GDP进行预测，预测结果见表5。

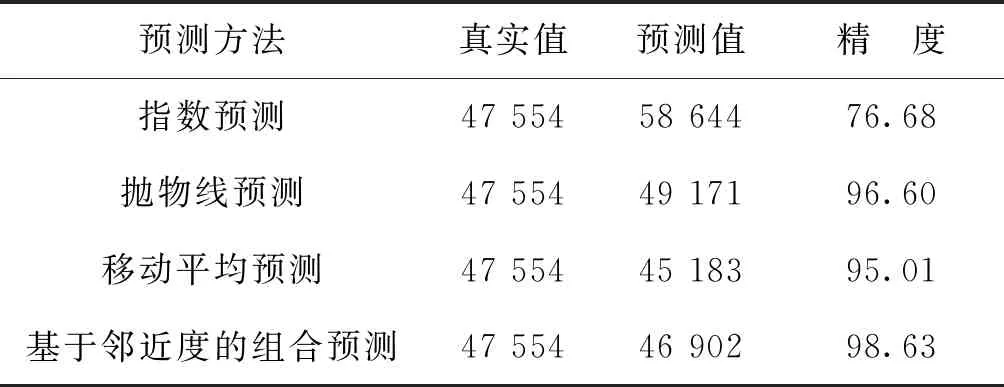
表 4 2018年安徽省人均GDP真实值与各方法预测值及精度

表 5 2019—2021年安徽省人均GDP预测值

3 结束语

从组合预测结果来看2019、2020、2021年较前一年安徽省人均GDP增长率分别为7.31%、6.64%、6.06%，人均GDP呈逐渐增长趋势，但增速逐渐放缓，符合目前我国对GDP增速的预期。由于我国在未来几年内处于深化供给侧改革时期，国内经济面临去产能、去库存、去杠杆、降成本、补短板五大任务。所以各地都在进行新旧动能接续转换，减少低端和无效供给的经济转型，更加注重新增长点、新动能和新供给，所以此时人均GDP增速稍有放缓，同时中国已是GDP排名第二的经济大国，各地巨大的GDP基数也会导致GDP增速放缓。因此，所建立的组合预测结果具有实际意义，与我国国情及安徽实际情况相符，对于研究未来安徽省人均GDP具有参考价值。