基于稀疏自编码的手指静脉图像分割*
2019-08-27秦华锋
秦华锋, 刘 霞
(1.重庆工商大学 计算机科学与信息工程学院,重庆 400067;2.重庆工商大学 智能制造服务国际科技合作基地,重庆 400067)
0 引 言
近年来,随着计算机以及网络技术的迅速发展,信息安全变得越来越重要,社会对信息安全的要求在不断提高,企业对信息安全的保护意识也在不断加强,身份识别系统也就应运而生。当前,个人身份鉴别主要依靠ID卡和密码等方式,但这些方式存在着容易丢失、遗忘、被复制和破解等安全性差的问题[1]。因此,生物特征识别技术作为一种更加安全可靠的身份识别方法,逐步取代了传统的身份识别方式[2]。在生物特征识别方式中,有指纹识别[3]、掌纹识别[4]、面部识别[5]、虹膜识别[6]、静脉识别[7]等。由于手指静脉存储于手指内部,不易被盗取,识别时接触少甚至勿需接触,且活体才能检测到静脉图像特征,因此手指静脉识别具有更高的安全性。
由于手指静脉图像质量受多种因素如环境光、环境温度、光散射的影响,因此手指静脉识别是一个挑战性的问题。在实际应用中,这些因素很难克服,所以许多手指静脉图像中包含了大量噪声和不规则的阴影。一般而言,匹配噪声和不规则的阴影区域会产生大量的匹配误率,降低了系统的认证精度。目前研究者们提出了大量的方法来分割手指静脉特征。例如2004年,Miura等[8]观察静脉横截面中像素灰度值的分布呈谷形状,提出利用重复线性跟踪法提取手指静脉轮廓。为了分割出更为鲁棒的静脉特征,提出了最大曲率算法[9],该方法主要通过计算静脉图像横截面轮廓局部最大曲率来提取静脉纹路。2006年,Zhang等[10]认为静脉特征在局部区域内可近似为一条直线,并构建了具有线性感受野的局部互联神经网络,以检测小区域中的直线特征,然后通过旋转图像提取不同方向上的静脉特征。为了提取连续的手指静脉特征,Qin等[11]在区域生长的基础上,提出了一种手指静脉纹理分割算法。同样地,该方法通过检测静脉区域横截面的谷形来提取静脉特征。实验结果表明:该算法能够提取到连续的手指静脉特征。2012年,Kumar等[12]将Gabor用于增强线性的手指静脉特征,并利用数学形态学方法对增强图像特征进行开闭预算得到粗细相同静脉纹路。最后,利用阈值对其进行分割得到静脉特征,其实验结果证明了该方法的有效性。2017年,Qin等[13]提出了一种基于Radon变换的手指静脉特征提取算法。通过计算Radon空间中曲率,静脉被有效地提取,同时噪声得到有效的抑制。2018年,Yang等[14]通过对静脉解剖机构的分析,提出了一种手指静脉分割算法,得到了良好的识别效果。
目前的手指静脉图像分割算法在静脉纹理的分割方面展现出不错的效果,但他们都假设静脉特征分布呈谷形状或者在局部区域呈一条直线,并设计了一些算法去检测它们,从而实现对静脉特征的分割。因此,上述的分割算法都存在以下的不足:由于人的先验知识有限,静脉像素的分布各种各样,不仅是谷形或者直线,所以基于这些假设的方法很难有效地提取手指静脉特征;当手指静脉像素呈现的分布较复杂时,很难建立有效的数学模型来检测该分布。
近年来,深度学习如深度自编码器具有强大的特征表达能力,已经受到广泛的关注。目前深度学习已经应用于计算机视觉中,并展现出了良好的性能。因此,首次将深度自编码器用于手指静脉特征分割中,提出了一种基于自编码的手指静脉纹路分割算法。首先,提出了一种自动标注方案对手指静脉像素点进行标注。即使用传统分割算法对原始静脉图像进行分割得到二值图像,并利用分割的图像对原始图像的静脉点进行标注。然后,以原始图像中的每个像素为点中心,得到多个相互重叠的小块。每个块的标签(静脉或者背景)为二值图像中对应位置的像素值。最后,根据块和对应的标签建立训练集合实现对自编码器的训练。在测试阶段,对于一幅输入图像,以每个像素点为中心,得到不同的块,并将它们分别输入到自编器中以预测该块中心点为静脉特征的概率。当对输入图像的所有像素点进行预测后,得到一幅概率图,再将其二值化后得到静脉特征。在公共数据库上的实现结果表明,提出的方法能够有效提取静脉特征,提高手指静脉识别系统的认证精度。
1 基于自编码器的手指静脉分割算法
为了提取到更为鲁棒的静脉特征,提出了基于自编码器的手指静脉分割算法。首先利用传统的图像分割算法对每个像素点进行标注。然后,把原始图像进行分块,构建训练集合。利用训练集中的图像块对自编器进行预训练。再利用二值图像对每个块进行标注,并用softmax函数替换自编码器的输出层,构建神经网络,最后使用保存的模型对测试图像进行分割得到静脉特征图像。算法流程如图1所示。

图1 算法流程图Fig.1 Algorithm flow chart
1.1 图像的标注
目前许多的图像分割算法[15-18],都是用手动标注的标签去训练神经网络以提取特征,然而这种手动标注的代价很高且容易出错。因此为了克服这个问题,提出了一种自动标注的方式。即对于给出的一幅图像,如图2(a)所示,通过传统分割算法(如最大曲率点分割)提取静脉特征得到二值图像如图2(b),对于二值图像中的每个像素P(x,y),可以将其值视为标签,其中静脉像素(白色区域)的值为1,背景像素(黑色区域)的值为0,如图2(c)所示。
以如下的方式标注原始图像像素(x,y)的标签L(x,y)。

(1)

(a) 原始图像 (b) 提取的静脉特征 (c) 标注静脉和背景
图2 标注静脉和背景像素
Fig.2 Labeling veins and background pixels
基于标签,可以将原始图像划分为大小为N×N的不同块,这些块作为稀疏自编码的输入可以提取静脉特征。
1.2 稀疏自编码器原理
稀疏自编码器(Sparse Auto-Encoder, SAE)是在自编码器的基础上加上稀疏表示的限制条件组成,对网络的隐含层输出有了约束,使得大部分隐含层神经元都处于非激活状态。自编码器的基本思想是尽可能复现输入信号,由三层的前馈神经网络构成,第一层到第二层相当于一个编码过程,第二层到第三层相当于一个解码过程,通过解码器重构特征与原始特征之间近似的优化条件来进行非监督训练。自编码器的形象表示如图3所示。通过训练可以得到较优的权重和偏置以及较小的误差。

图3 自编码器的形象表示Fig.3 Visualised expressin of auto-encoder
算法步骤[19-21]如下:
Step1编码与解码。
将原始数据x={x1,x2,…,xn}通过线性函数和sigmoid激活函数,映射到隐含层得到编码结果y={y1,y2,…,ym},即:
(2)
将编码结果y通过线性函数和sigmoid激活函数,映射到重构层得到解码结果z={z1,z2,…zn},z的维度与原始数据x的维度一致,即:
(3)
其中,y为编码后的数据,即原始数据的特征表达,z为解码后的数据,w1、w2、b1、b2分别为输入层到隐含层、隐含层到重构层的权重及偏置。
Step2构造代价损失函数J(w,b)。
当神经元的输出接近1的时候认为它被激活,当神经元的输出接近0的时候认为它被抑制,使得神经元大部分时间都是被抑制的限制称作稀疏性限制,通常是在隐含层神经元的数量大于输入层神经元数量时使用。
首先计算隐含层第i个神经元的平均活跃度:
(4)
其中,N为样本个数,ρi为编码层的第i个神经元的平均激活度。其次加入一条限制:
ρi=ρ
(5)
使得隐含层第i个神经元的平均活跃度接近ρ,其中ρ是稀疏性参数,通常是一个接近0的较小值。
然后,为了实现上述的限制,需要加入一个惩罚项:
(6)

最后构造代价损失函数J(w,b),其中w={w1,w2},b={b1,b2}:
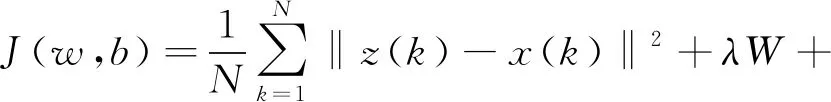
(7)
(8)

Step3通过梯度下降算法优化代价损失函数及参数w,b。
(9)
(10)
(11)
(12)
其中,x(k),z(k)为第k个原始数据和重构数据,wk,bk分别表示第k个数据的权重与偏执,α表示学习率。
1.3 稀疏自编码器的训练和测试
首先,构建稀疏自编码模型并把训练集分成不同的子集合,分批次输入到SAE中。当网络进行一次前向传播后,得到更新的权重和偏置,通过反复迭代寻找权重和偏置的最优解,当精度满足要求时,停止迭代,从而完成本次深度置信网络模型的训练。采用的SAE结构如图4所示,包含输入层、一个隐含层和输出层。其中输入层神经元数为121,隐含层神经元数为100,输出层神经元数为121,权重初始值随机化为(-1,1),稀疏系数置为0.1。
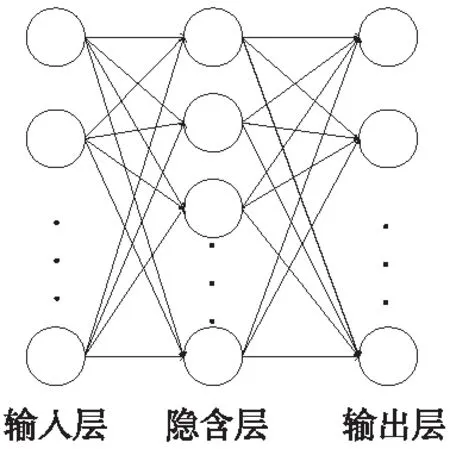
图4 SAE结构图 Fig.4 The structure of SAE
1.4 神经网络的训练和测试
首先,在SAE网络结构中增加一个softmax分类器构建一个神经网络,利用SAE训练的权值初始化,把带标签的训练图像输入到其中进行训练,当网络进行一次前向传播后,计算梯度并进行反向传播以更新滤波器权值和偏移量,通过反复迭代寻找滤波器和偏移的最优解,当精度满足要求时,停止迭代,从而完成本次深度神经网络模型的训练。采用的神经网络结构如图5所示,包含输入层、一个隐含层和输出层。其中输入层维数为121,隐含层维数为100,输出层维数为2(类别数)。

图5 神经网络结构图Fig.5 The structure of neural network
1.5 静脉特征编码 (二值化)
在实验过程中,虽然静脉块和背景块像素分别被标注为1和0,但神经网络的输出F(x,y)是一个0到1的概率值。为了实现对图像的匹配,采用下面的等式对静脉特征进行编码。其中R(x,y)是图像F(x,y)得到的编码结果。

(13)
1.6 匹配
为了实现认证, 需要计算两幅图像的相似性。假设E和F分别表示一副注册图像和测试图像,它们的高和宽分别为x和y。将注册图像E的宽度和高度分别扩展到2w+x和2h+y,它的扩展图像如下:

(14)
注册图像E和测试图像F的匹配距离可以由式(15)计算:

(15)
其中,

(16)
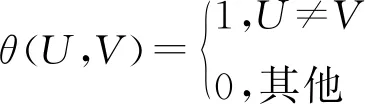
(17)
2 实验结果及分析
为测试本文算法的性能,利用香港理工大学的手指静脉图像数据库进行了实验。在对比性试验中,重复了两种经典的手指静脉图像分割算法,即重复线性跟踪法[8]和最大化曲率点方法[9],也比较了当前成熟的手指静脉图像分割算法如基于Gabor的分割算法[12],以更有效地估计本算法的识别性能。
2.1 手指静脉数据库
数据来自香港理工大学的手指静脉图像数据库。该数据库分了两阶段采集,第一阶段采集了320个个体各6张手指静脉图像,第二阶段采集了210个个体各6张图像,每幅图像分辨率为364×97像素。为了保持静脉图像数据的一致性,采用前210个个体采集的图像,即210×12=2 520幅,同时把前105个个体产生的1 260幅图像作为训练集,后105个个体产生的1 260幅图像作为测试集。
2.2 训练集合和测试集合的构建
对分割后的二值图像进行分块操作,以获得训练集和测试集。其中块的大小为11×11,滑动间隔为5。进行图像块采样,以块的中心点是否为静脉作为块的标签,当静脉和非静脉块各采样5万张时停止采样,以得到10万个训练集样本。在测试阶段,将一幅图像以每个像素点为中心,得到一个11×11的小块,然后将其输出到神经网络中得到该中心像素点为静脉特征的概率。计算所有像素点的概率后得到一幅概率图谱,利用式(13)将其二值化,提取出静脉特征。
2.3 参数的选取
在实验中,就SAE对改进手指静脉图像分割的效果进行了检测。如果SAE的参数如层数、节点数不确定,将不能全方面地提取数据集的特征,从而影响分类准确性。同时,如果块的大小不确定,也会对SAE的算法产生影响。为了检验算法的效果,同时也使SAE选择合适的参数,选用基于Gabor的分割算法并在测试集上进行了以下几组实验。
2.3.1 层数的选择
为了检验稀疏自编码器隐含层数对检测效果的影响,将SAE中其他参数固定,学习率设为0.1,节点数为100,稀疏惩罚系数为0.1,然后改变隐含层的层数。不同隐含层数SAE的误差EER如表1所示。由表1可知,当隐藏层数为1时,本文方法在测试集中具有最小误差。

表 1 隐藏层数的选择
2.3.2 隐层节点数的选择
当确定了最佳隐含层数后,再确定SAE隐含层节点数。首先SAE的隐含层数固定为1,学习率为0.1,稀疏惩罚系数为0.1。然后选取神经元个数为50、100、200,实验结果如表2所示。由表2可知,随着隐含层神经元数的增多,误差EER呈现先降低后升高的趋势,因此当隐含层神经元数为100时,测试集误差最小。

表 2 隐层节点数的选择
2.3.3 块大小的选取
为了验证不同块大小对稀疏自编码器结果的影响,选取块的大小为7×7、11×11、15×15、19×19并进行实验,实验结果如表3所示。由表3可知,不同块设置从小到大的实验误差呈现先降低后升高的趋势,当块大小设置为11×11时,测试集的误差最小。
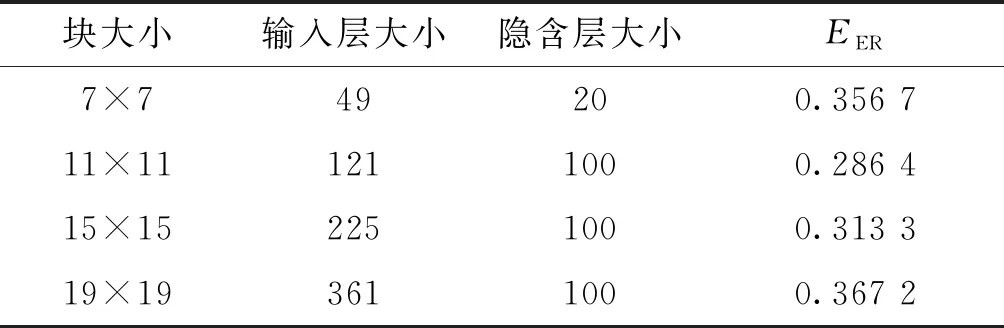
表 3 块大小的选取
2.4 评价指标
为了检验算法的效果,计算了各种分割图像的认假率(False Acceptance Rate, FAR),拒真率(False Reject Rate, FRR),并利用等误率(Equal Error Rate, EER)[22]来对算法进行评价。
(18)
(19)
其中,NF表示非法匹配分数的数量,NT表示合法匹配分数数量,NFT表示非法用户被误认为合法用户的数量,NTF表示合法用户被误认为非法用户的数量。等误率是当认假率与拒真率相等时的误率。
2.5 实验结果
2.5.1 分割结果
为了从视觉上分析算法的性能,分别利用重复线性跟踪法[8]、最大化曲率点方法[9]、基于Gabor的分割算法[12]对手指静脉图像进行分割。另外,将3种分割的结果作为标签建立训练集,进行训练,实现静脉特征的分割和认证。为了便于描述,将利用3种分割算法训练本文的方法分别表示为 “重复线性跟踪法+本文算法”、“最大曲率点分割算法+本文算法”、“基于Gabor的分割算法+本文算法”。3种已有的方法和本文方法的分割结果如图6所示。

图6 不同算法的分割效果Fig.6 Experimental segmentation results from various approaches
从分割结果可以看出,相比目前的算法,该方法有效地抑制了模糊区域的噪声,能够有效剔除伪静脉特征,使得提取的静脉特征更加平滑连续。
2.5.2 认证结果
为了估计本算法的识别性能,首先利用基于稀疏自编码的分割算法对图像进行分割和匹配,然后计算等误率。同时,实验给出了3种基于手工特征的分割算法如重复线性跟踪法[8]、最大化曲率点方法[9]、基于Gabor的分割算法[12]的识别性能。在数据库中,总共有105根手指的数据,每根手指在两个阶段提供了12幅图像,每个阶段提供6幅。对于每根手指,选取在第一个阶段采集的6幅图像作为注册图像,剩下的6幅图像作为测试图像。匹配同一根手指在两个阶段的图像可以得到6个合法匹配分数。因此,105根手指产生630个(105×6=630)合法匹配分数。匹配两幅来至不同手指的图像产生非法匹配分数。因此,这里有105×104×6/2=32 760个非法匹配分数。最后,利用合法匹配分数和非法匹配分数计算等误率,并以合法匹配为横坐标,非法匹配分数为纵坐标绘制ROC曲线。实验结果如表4和图7所示。

表 4 不同分割算法的EER比较

图7 ROC曲线
Fig.7 ROC curve
从ROC曲线和等误率结果可以看出,通过稀疏自编码器改进后的分割算法效果优于传统的分割算法。例如,改进后的基于Gabor分割算法的等误率为2.3%,比改进前效果提高了大约30%;改进后的重复线性跟踪法的等误率为8.5%,比改进前效果提高了大约29%,这可能归结于两个原因:
其一是由于基于手工特征分割的方法独立地对每幅图像进行分割,所以它们并不能从不同图像中获取用于分割静脉特征的知识。相反地,利用不同的图像建立一个大尺度的数据集(10万个训练集样本)来训练本文的模型,使得提出的模型能够充分地从不同图像中获取到用于静脉特征提取的先验知识。因此,即使自动标注方案可能导致少量的错误标签,本文方法也能够有效预测像素点为静脉的概率。
其二是当给定学习目标(样本的标签)后,深度自编码器通过学习表达提取到与目标相关的高层次的特征。由于手工特征在提取过程中可能丢失一些有用相的信息,而SAE直接通过最小化与目标的误差学习到高层次的特征,所以本文方法得到的特征更为完备。
3 结束语
图像分割是手指静脉识别技术中的重要环节,为了提高图像分割的效果,提出了基于稀疏自编码器的手指静脉图像分割算法。提出的分割算法在原有分割的二值图像基础上进行了图像的标注、自编码器和神经网络的训练,最后再进行图像分割得到分割图像。通过对比基于Gabor的分割算法、最大曲率点分割算法、重复线性跟踪法这3种分割方法,发现改进后的分割算法的等误率均比改进前的低,说明改进后的分割算法更加有效地提取到了手指静脉特征,这对手指静脉识别是更有意义的。
