带电粒子在时变电磁场下的运动*

王 荣 秀

(重庆工商大学 计算机科学与信息工程学院，重庆 400067)

0 引 言

带电粒子在电磁场中的运动一直是电磁理论的核心问题之一，涉及诸多不同的应用领域，如电/磁分离器、质谱仪、电泳镀膜、电/磁加速器、等离子体激光相互作用等，因此研究电荷在电磁场的运动具有非常重要的实际意义[1-2]。一般情形下，电荷在电磁场中的运动十分复杂。目前的参考文献中, 对带电粒子在电磁场中运动状态的描述主要是针对静场以及仅有电场或磁场等一些特殊情况[3-8]，很少对带电粒子在时变电磁场中的运动进行一般的分析。经典情形下，带电粒子的运动由洛伦兹力方程(简称洛伦兹方程)描述，对带电粒子运动的分析首先是对洛伦兹方程求解；由于方程中存在耦合项，而且在交变时引进的含时变量使求解困难。Chang等[9]利用本征值分解来求解洛伦兹方程，把解表示成矢量的积分形式，但要得到积分的结果同样困难。之后，Donkov等[10]简化了电磁场矢量的表达式，应用微分方程解的叠加性，先后求出齐次通解及特解来得到方程的解。该方法得出了洛伦兹方程解的一般形式，但不足之处是对电/磁分量的假设条件限制了解的应用范围，而且特解的求取较为复杂。

由于平面波及正交时变电/磁场是较典型的交变电磁场形式，因此主要对带电粒子受平面波交变电磁场及正交时谐电/磁场作用下的运动规律进行探讨，通过求解经典洛伦兹方程，分析带电粒子的运动特性，并对几种常见的情况进行讨论。

1 正交时谐电场与磁场下洛伦兹方程的解

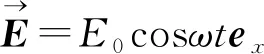
(1)

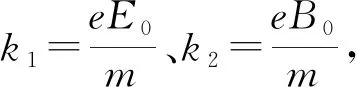
(2)

由式(2)可以看出，粒子沿y轴运动不受影响，保持匀速直线运动；而在x、z轴方向由于耦合项的存在，运动相互影响。消去时间因子cosωt后可得：

(3)

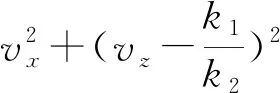
经过积分也可得到式(3)。磁场虽然不直接做功，但能改变运动速度的方向，使vx和vz的大小发生变化，从而影响电场做功。

V=XΦ1+YΦ2

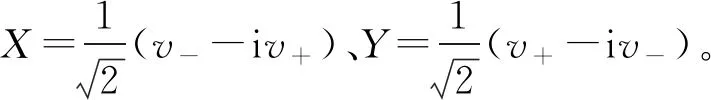
(4)

(5)

(6)

利用式(5)、式(6)讨论几种常见情况：

认知行为治疗，人际心理治疗，行为心理治疗，都对抑郁症有确定的疗效。其他类型心理治疗的证据少。有一些比较研究表明认知行为治疗和第二代抗抑郁药物具有相似疗效，而副作用可能更低，此外，使用认知行为治疗所报告的抑郁复发率低于第二代抗抑郁药物治疗。因此，尽管第二代抗抑郁药物通常是针对抑郁症患者开出的初始治疗方案，CBT依旧可作为初始治疗的合理疗法，并应该被认为是可用的第二代抗抑郁药物的替代治疗方法。

(a)速度随时间的变化 (b)速度关系

图1 静场条件下粒子沿x、z轴的速度变化与相互关系
Fig.1 The velocities of particle in static fields andtheir relations

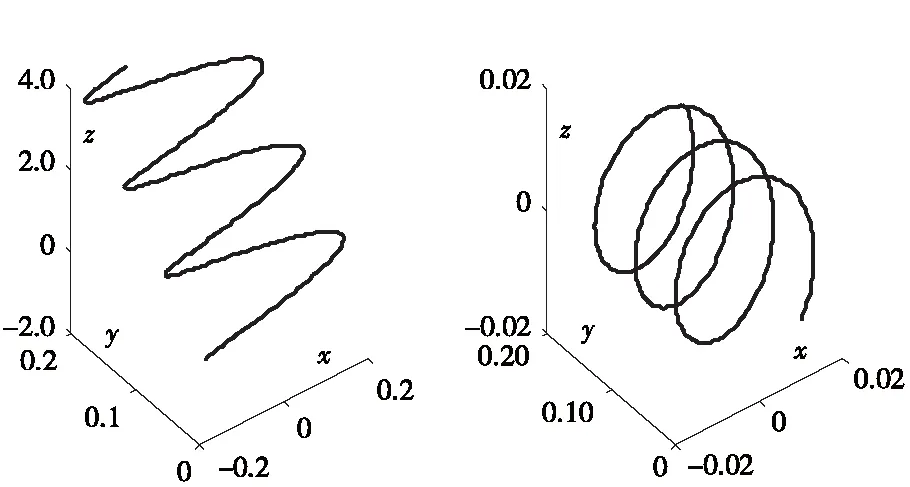
(a)静场时粒子运动轨迹 (b)仅有稳恒磁场时粒子的螺旋运动

图2 粒子静场下的运动轨迹
Fig.2 Particle trajectory under static field

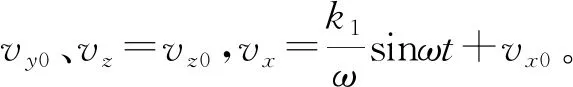
(a)仅有时变电场时粒子的运动 (b)仅有时变磁场时的运动

图3 粒子在时变电或磁场下的运动
Fig.3 Movement with alternating electricfield and magnetic field

总之，带电粒子的运动与初始速度、电/磁矢量的大小和方向、频率等因素有关；无论静场还是时变场，沿电场方向和磁场垂直方向都存在周期往返性质的运动。其变化频率在静场时取决于磁场的强弱，在时变场时则主要由场的变化频率决定。当场的变化频率很高时，粒子运动中的周期性成分很小，接近直线运动。

2 平面波场下带电粒子的运动

(7)

(8)

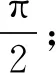
(9)

当然vx并不具有波动性质，式(9)只是反映了vx随时空的分布和变化特性。对于方程式(7)、式(3)依然成立，设粒子速度不超过波速u，因此有：

由于vx具有周期分布和变化的特点，因此vz也具有周期分布和变化的特征，但并不满足波动方程，而是满足

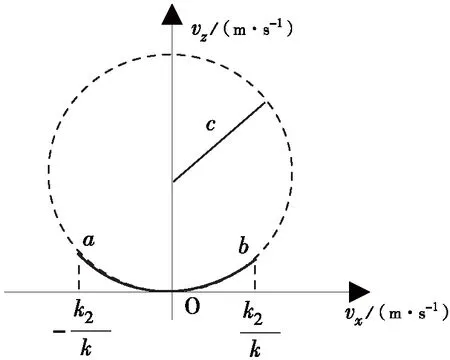
图4 vx和vz的关系Fig.4 The variation of vx and vz

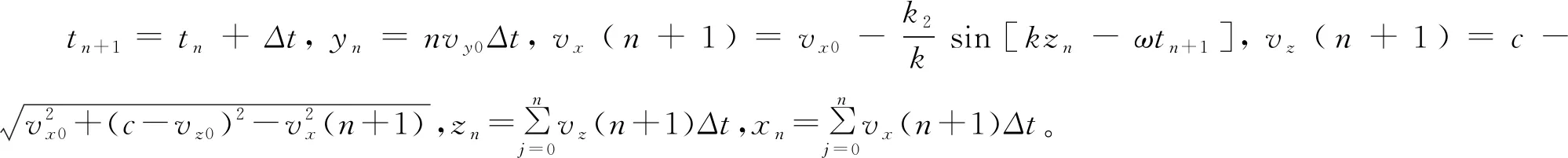
从图5中可以看到，质子主要在x方向有往返运动，且速度明显大于其他方向，vx和vz的关系与图4相同。随着z值增加，曲线被拉伸。另外，质量的减小，可以使k2较大，因此vx和vz可能变得很大，此时粒子的坐标z变化较快，沿x轴的运动会不同。作为比较，考虑电子的运动，e=1.602×10-19C，m=9.1×10-31kg，模拟结果如图6、图7所示。

(a)平面波场下质子vx和vz的关系 (b)平面波场下质子三维运动路径

图5 质子的速度及运动轨迹
Fig.5 The velocity and trajectory of photon

(b) 电子沿x轴的速度

(a) 电子沿x轴的位移

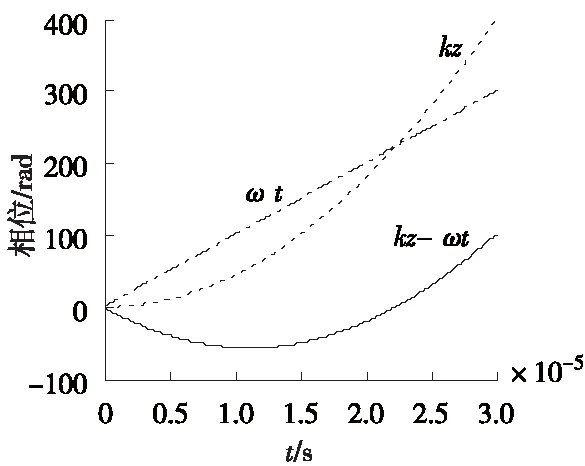
(b) vx的相位变化

图6(a)显示，粒子沿x方向运动的周期是变化的，在t≈1.2×10-5s时，有一个明显的频率延缓，由于速度较大，从而使x方向位移产生较大变化,如图7(a)所示；此时vx的相位因子kz-ωt在t≈1.2×10-5s附近有驻点，如图7(b)所示。这主要与参数k2、波频ω(或波矢k)有关。当k2较小(m、B0较小；k较大)，vx和vz很小，粒子沿z轴位移缓慢，相位因子kz-ωt中ωt起主要作用，不出现极值驻点；而当k2较大时，粒子沿z轴运动速度很大，kz变化很快，可能使相位因子kz-ωt产生驻点，从而导致位移的突变。理论上，kz-ωt的驻点意味着vz接近光速，这实际上是不可能的，此时应考虑粒子的量子和相对论效应[11]。另一方面也说明：经典洛伦兹方程不适于描述电子等质量较小的带电粒子在高频且较强电磁场下的运动,当然这与经典电磁理论的局限性是一致的。

3 结束语