特定地质条件下水库蓄水坝基变形特征分析

陈 凤，王 鹏

(1.江西省水泰工程检测有限公司，江西 南昌 330000；2.湖南省株洲市佳联建设工程有限公司，湖南 株洲 410004)

坝基抬升变形在国内外水利水电工程中相对少见。国内的澧水江垭大坝[1-2]、大渡河铜街子大坝[3]、金沙江向家坝[4]及小湾特高拱坝[5]等水利工程都出现过坝基或近坝山体抬升变形现象。其中铜街子水电站坝体右岸山体表面产生24.3～28.9 mm抬升位移，如此大的抬升位移量实属罕见。国外的托克托古尔重力坝[6]、英古里重力坝[7]也监测到了坝基及水工建筑物抬升变形现象。

坝基抬升变形的形成原因相对复杂，受蓄水条件、水文地质及水工建筑物等因素的综合影响，如何合理解释抬升变形的原因，国内外学者展开了大量研究，取得了诸多成果。王兰生[8]等对坝基岩体的扩容行为开展室内试验，认为蓄水使得承压含水层D2y内的孔隙水压力增高是坝基抬升的主要原因；伍法权[9]等基于实测资料，提出了5种引起抬升变形的主要影响因素，认为水库蓄水是直接影响因素；祁生文[10]等采用数值方法模拟江垭大坝的抬升变形过程，认为造成抬升变形的主要外在条件是水库蓄水；唐国进等[11]对监测资料进行了详尽的分析，提出多种抬升变形可能的诱发原因，并预测变形会逐步趋于稳定；Xiaoli Liu[12]等认为坝基强度参数的弱化以及构造应力等因素也会对抬升变形产生影响；蒋中明等[4]采用数值方法探讨了坝基水文地质条件对抬升变形的影响，胡波、吴中如[5,13]等结合原型监测数据，采用数值仿真对小湾特高拱坝坝基岩体变形特性进行了分析，认为坝踵基岩抬升主要是由于库水位的持续升高，水推力作用逐渐增大，受弯矩作用坝体有向下游方向转动的趋势，坝踵压力减小，进而致使坝踵基岩产生抬升变形。

可见，在抬升变形成因问题上已有比较统一的结论,即产生抬升变形外因是水库蓄水，而内因则是坝基岩层存在特殊地质构造或特殊岩层(比如下伏有承压含水层或遇水膨胀岩层等)，但对外因(如蓄水水位等)和内因(如坝基岩体变形模量、渗透系数)敏感性影响研究少有提及，因此有必要对这一方面进一步研究。本文基于流固耦合作用的抬升变形数值理论，建立特定地质条件下的二维数值模型，研究蓄水水位、岩体变形模量及渗透系数对抬升变形的影响规律，进一步揭示抬升变形的变形机理。

1 基于流固耦合作用的抬升变形数值理论

对于流固耦合理论的研究已有诸多成果[14-16]。对于裂隙岩体，考虑有效应力影响及孔隙水压力的一般应力应变关系可表示为：

εij=(1+γ)/E·σij-γ/E·σkk·δij-

α/(3H)·p·δij

(1)

式中εij——应变分量；σij——应力分量，Pa；σkk——正应力，Pa；E——弹性模量，Pa；γ——切应变；δij——克罗内克符号(i=j时，δij=1；i≠j时，δij=0)；α——比奥系数[14]，可取α=K/H；K——固体介质的有效体积模量，Pa；H——比奥常数；p——孔隙压力，Pa。

不计体力和惯性力时的平衡方程为：

σij,j=0

(2)

应变-位移关系为:

εij=1/2·(ui,j+uj,i)

(3)

式中u——位移,m。

将式(1)、(2)代入式(3)，可得孔隙介质固体变形控制方程为：

G·ui,ij+(λ·G·uk,kl)+α·pj=0

(4)

式中G——剪切模量，Pa；λ——拉梅常数。

对于流体相，达西流速[15]为:

vi=-(k/μ)·p,i

(5)

式中v——流体速度，m/s；k——渗透率，m2；μ——流体黏滞系数，Pa·s。

根据流体流动的连续性,即流体速度的散度等于单位体积空间流体储量的比率，有:

vj,i=φεkk-c*p

(6)

式中φ——孔隙度；c*——集总可压缩性。

将式(5)代入式(6)得到渗流控制方程：

-(k/μ) ·p,kk=φεkk-c*p

(7)

式(4)、(7)为等效孔隙连续介质与变形有关的流动控制方程。

渗流场和应力场全耦合的过程是一个动态的过程，其求解需借助有限元等数值方法完成。本文采用有限差分软件FLAC3D[16]对抬升变形过程进行模拟。为实现耦合过程中渗流场和应力场之间的相互耦合，FLAC3D将孔隙水压力和饱和度作为节点变量，依赖于流体连续性方程的有限差分节点表达式，以力学平衡作为起始状态，通过若干流体步及力学步相互转换循环计算，达到系统计算平衡；通过流体步得出孔隙水压力增量，力学步得出体积应变[12]。从而计算出计算模型整体渗流场及应力应变场分布。

2 数值模型

2.1 计算网格

由文献[4，8-9]研究成果可知，江垭大坝水文地质条件是产生抬升变形水文地质条件的典型代表，在这种特定地质条件下，由于水库蓄水对岩体的外在渗透力，从而导致坝基岩体产生抬升变形，其地质剖面见图1。坝基分布有厚度不均的含水层和相对隔水层，其中坝基上游分布有厚度173 m的承压热含水层(图1)；底部分布厚度67 m相对隔水层，位于灌浆帷幕下端；下部为岩溶含水层，厚度36.5 m。本文采用江垭水库大坝坝基水文地质模型，建立二维坝基岩体抬升的数值计算模型，分别研究蓄水水位、岩体变形模量及渗透系数对抬升变形的影响规律，从宏观上揭示坝基岩体抬升变形机理。

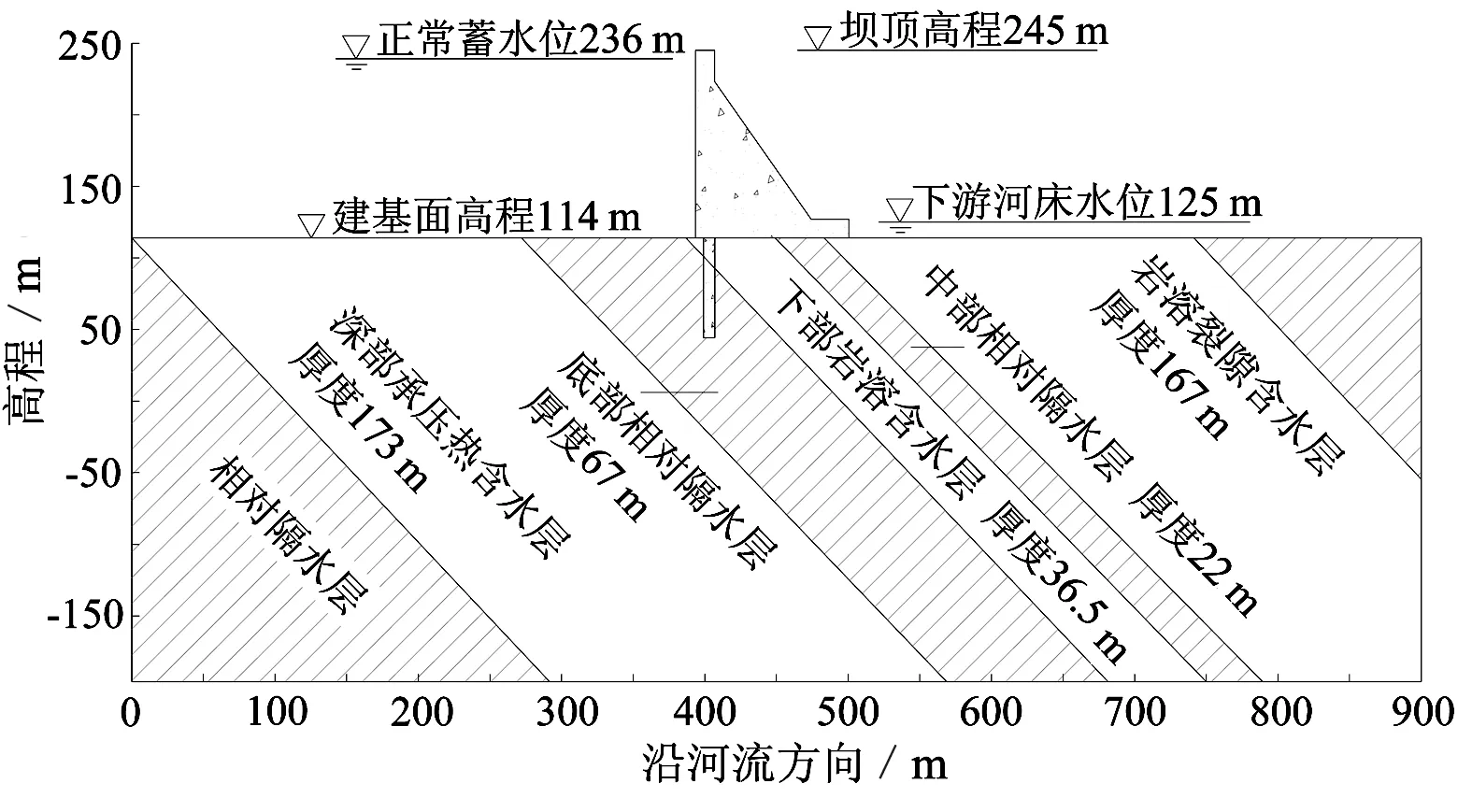
图1 江垭大坝坝基地质剖面

计算网格模型见图2，以坝轴线为起始，分别向上游截取500 m、向下游截取600 m作为计算模型的上下游竖向边界，沿x方向建立6个岩层，各岩层标号见图2。底部高程-200 m作为底部边界，大坝建基面高程114 m，坝顶高程245 m，坝基底宽102 m，模型在y方向拉伸30 m，划分3个单元。考虑坝基灌浆帷幕对抬升变形的影响，最大深度处在相对隔水层中，以起到隔水效果。采用六面体单元对模型进行网格剖分，网格单元总数4 962个，节点总数6 968个。

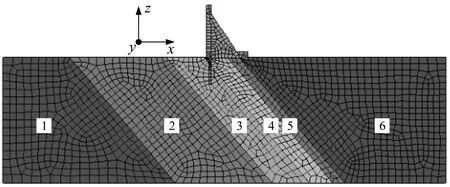
图中数字为岩层标号图2 数值计算网格

2.2 计算参数及边界条件

力学边界条件：底边界施加铅直向约束；左右铅直边界施加水平约束。上、下游库底施加应力边界；大坝上游面施加应力边界。水力学边界条件：模型底边界、左右铅直边界为不渗透边界；上下游库底为已知水头边界，大坝上游面施加水头边界。初始条件：初始渗流场按蓄水前河道水位高程125 m计算；初始应力场为建坝前的自重应力场。计算参数见表1。

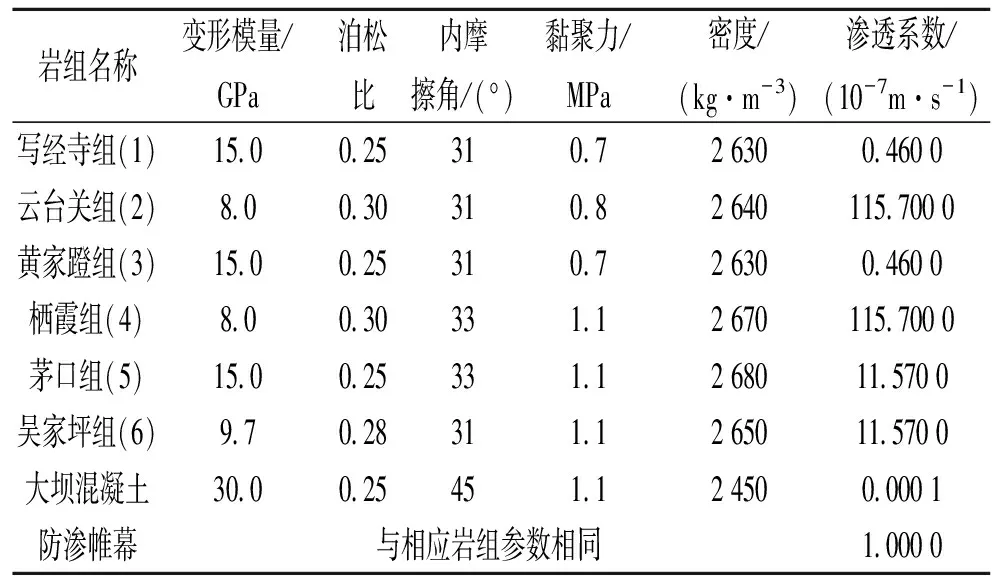
表1 数值计算参数

2.3 计算步骤

采用FLAC3D数值计算过程如下：①计算初始应力场，渗流计算功能关闭；②计算初始渗流场，力学计算功能关闭；③大坝一次性施工完成模拟，流固耦合计算；④水库蓄水，流固耦合计算。

2.4 计算方案

为了分析特定岩层水力学及力学参数变化对抬升变形影响，对大坝坝基在不同蓄水水位、坝基变形模量及渗透系数变化条件下的抬升变形进行敏感性计算。变形模量变化计算方案见表2，计算水位为236 m；渗透性变化计算方案见表3，计算水位236 m；水位变化计算方案见表4。

表2 变形模量敏感性计算方案

表3 渗透系数敏感性计算方案

表4 水位变化计算方案

3 计算成果分析

3.1 变形模量对抬升变形的影响

图3(a)—(f)为表2中6种计算工况下的铅直位移等值，其中等值线负值代表沉降变形，等值线正值代表抬升变形。由图可知，坝基不同岩层变形模量的变化对抬升变形最大位移量及变形区域影响很大。6个计算方案中，方案E1最大抬升值最小为3.76 mm，而方案E5最大抬升值最大为8.83 mm，6个方案最大抬升值及抬升区域见表5。

表5 不同变形模量方案计算结果统计

图4为6种计算工况的抬升变形分布，由图可知，随着坝基变形模量的减小，发生抬升位移的范围越大。虽然在相同地质构造模式和相同渗流场作用下，但是坝基岩体变形模量发生变化后，其所产生抬升变形的范围和最大抬升变形量均不相同。总体规律为：①坝基岩体变形模量足够大时，坝基不会产生抬升变形；②坝基岩体变形模量越小，抬升变形越大，抬升变形范围越大；③坝基地层岩体的变形模量组合方式不同，抬升变形大小及分布范围也不相同。

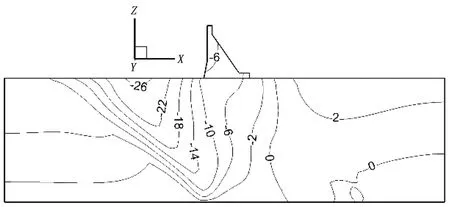
a) 方案E1

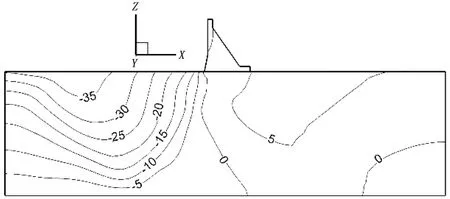
b) 方案E2

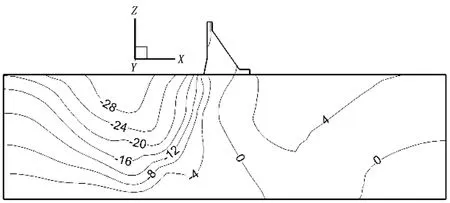
c) 方案E3

d) 方案E4图3 不同变形模量抬升变形(mm)

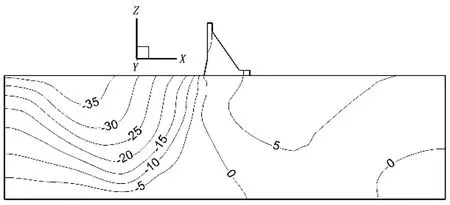
e) 方案E5

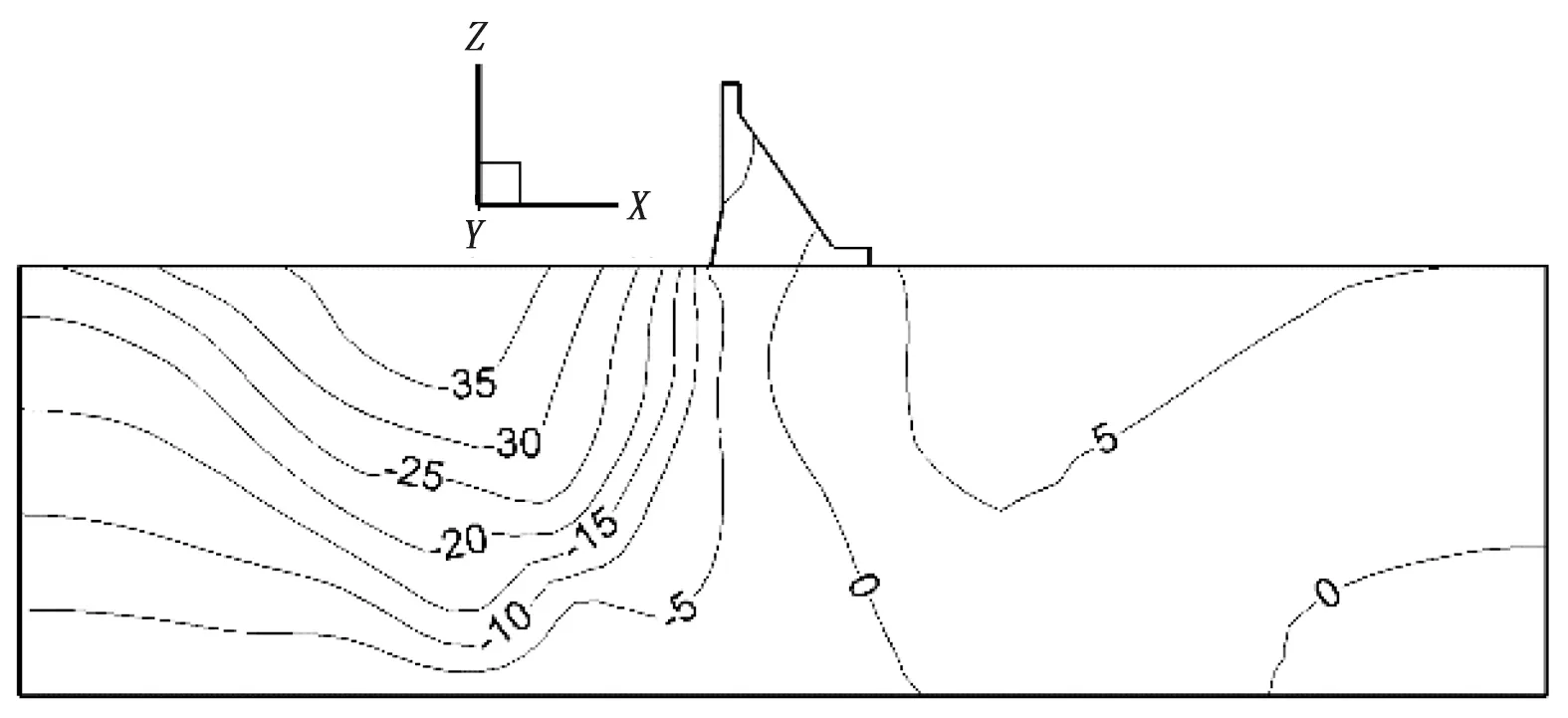
f) 方案E6续图3 不同变形模量对抬升变形(mm)

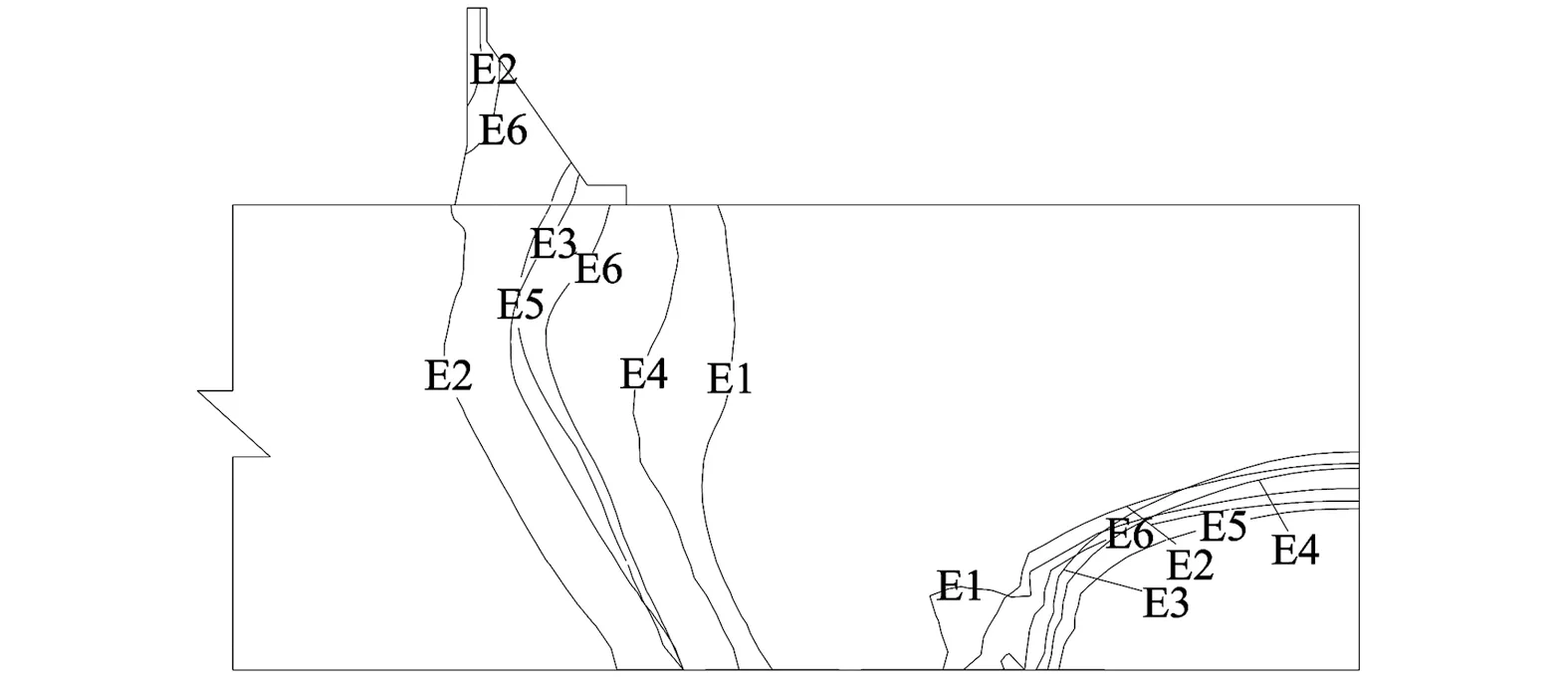
图4 方案E1—E6抬升变形分布范围

3.2 岩体相对渗透性对抬升变形的影响

为研究岩体渗透性大小对抬升变形的影响，以变形模量计算方案E7为基准工况，分别研究表3中各方案的抬升变形。图5(a)—(d)为4种计算工况下的铅直位移等值。由图可知，在不同的渗流场作用下及相同地质构造模式和相同力学参数条件下，坝基岩体产生抬升变形的范围和最大抬升变形量受渗流场的影响较大。4种计算方案中计算模型均出现抬升变形，其中方案K1最大抬升值最小为7.58 mm，而方案K2最大抬升值最大为9.08 mm，不同方案最大抬升值及对应抬升区域描述见表6。

图6为4种工况下的抬升变形分布。由此可见，渗流场变化条件下，抬升变形的规律性相对较差，总体上有以下认识：①坝基下存在相对隔水层的条件下，坝基会产生一定程度的抬升变形；②坝基岩体中渗透性差异不大的情况下，也可能产生抬升变形；③坝基地层岩体的渗透系数组合方式不同，抬升变形大小及分布范围也不相同。

a)方案K1

b)方案K2

c)方案K3

d) 方案K4图5 不同渗透系数对抬升变形的影响(mm)

表6 不同渗透系数方案计算结果统计

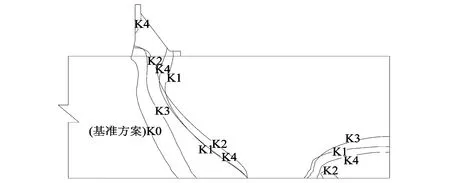
图6 方案K1—K4抬升变形分布范围

3.3 水库水位变化对抬升变形的影响

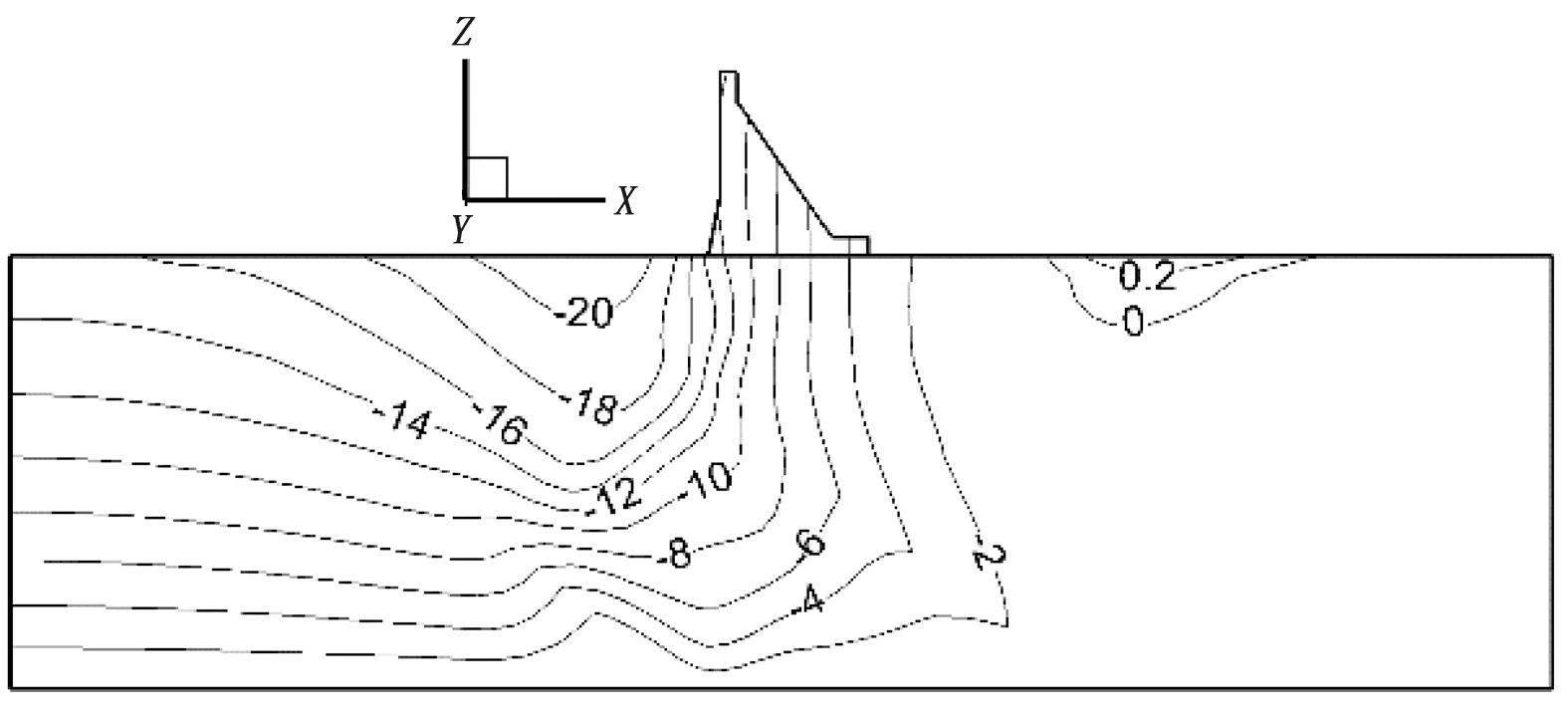
为研究水库蓄水高度对抬升变形的影响，以渗透性敏感计算方案K3为基准工况，研究表4中各方案的抬升变形。图7(a)—(d)为4种计算工况下的铅直位移等值图。由图可知，方案H1与方案H2计算模型并没有产生抬升变形，而方案H3下游河床发生抬升，最大抬升值0.34 mm；方案H4下游河床发生抬升，最大抬升值2.44 mm，各计算方案抬升区域描述见表7。

表7 不同水位方案计算结果统计

图8为H3、H4工况下抬升变形分布。由图可知，随着蓄水水位的增大，坝基抬升变形的位移量越大，且范围越广。在相同水文地质构造模式和相同力学参数条件下，水库蓄水水位不同，坝基岩体产生抬升变形的范围和最大抬升变形量不同。总体上有以下认识：①水库水位降低，坝基及河床抬升变形减小；②坝基岩体产生抬升变形，存在一个临界水库水位。水库蓄水水位大于临界蓄水位，坝基及下游河床将产生抬升变形；反之，当水库蓄水水位小于临界蓄水位，坝基及下游河床不会产生抬升变形。

a)方案H1

b)方案H2

c)方案H3

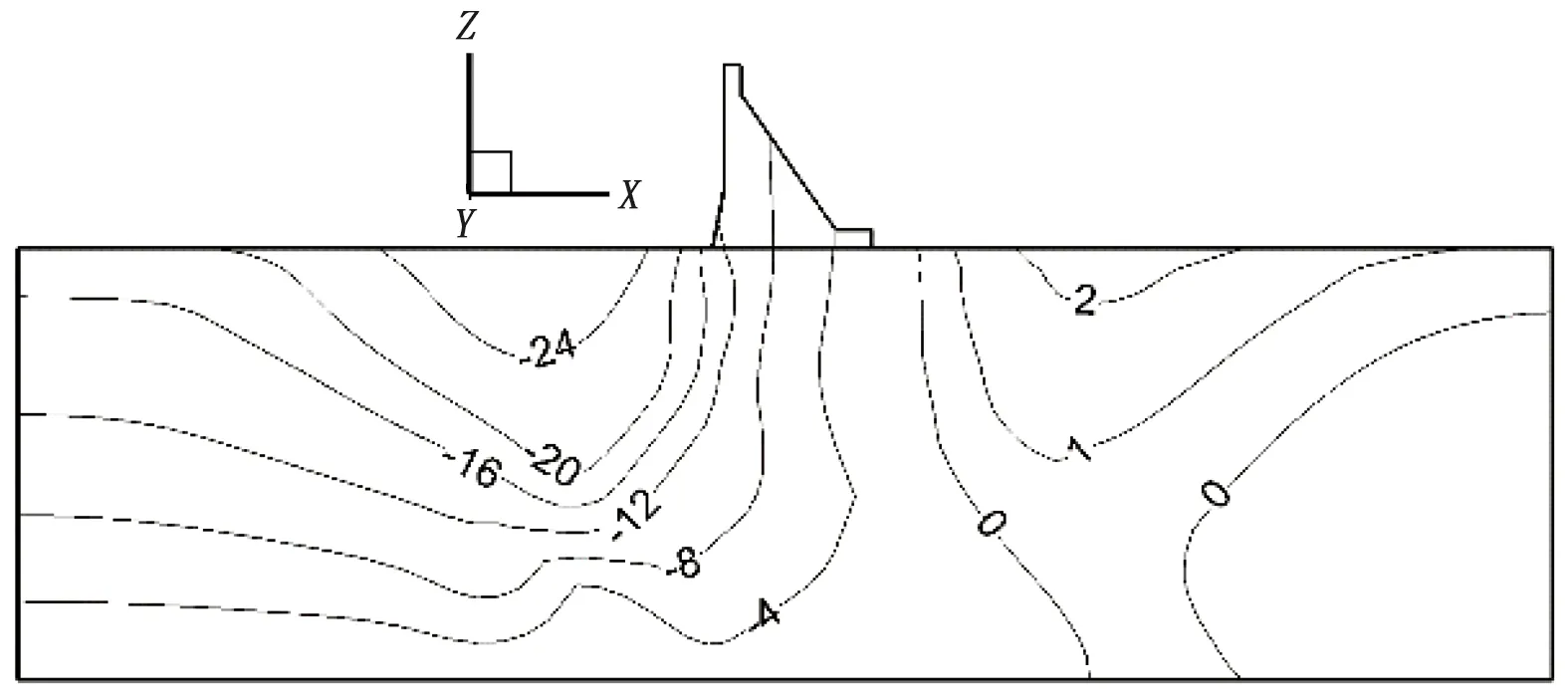
d)方案H4图7 不同蓄水深度对抬升变形的影响(mm)

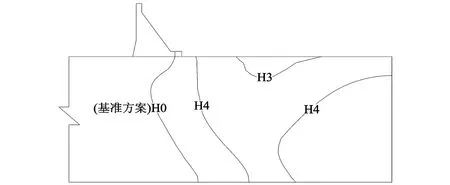
图8 方案H3、H4抬升变形分布

4 结论

为本文研究需要，以江垭大坝水文地质条件为典型建立FLAC3D数值模型，研究了特定地质条件下坝基不同岩层变形模量、渗透系数及不同蓄水条件等因素对抬升变形的影响，通过计算分析得到以下结论。

a) 坝基岩体变形模量足够大时，坝基不会产生抬升变形；坝基岩体变形模量越小，抬升变形越大，抬升变形范围越大；坝基岩体的变形模量组合方式不同，抬升变形大小及分布范围也不相同。

b) 坝基下存在相对隔水层的条件下，坝基会产生一定程度的抬升变形；坝基岩体中渗透性差异不大的情况下，也可能产生抬升变形；坝基岩体的渗透系数组合方式不同，抬升变形大小及分布范围也不相同。

c) 水库水位降低，坝基及河床抬升变形减小；水库水位大于临界水位，坝基及下游河床将产生抬升变形；反之，当水库水位小于临界水位，坝基及下游河床不会产生抬升变形。