汽车差速器锥齿轮差速工况下的润滑特性研究*

(青岛理工大学机械与汽车工程学院 山东青岛 266520)

汽车差速器是汽车重要的组成部分，在汽车的转向系统中发挥着重要的作用，能够保证汽车转向时内外轮速度差，避免轮胎在地面上的滑移和滑转[1]。现在汽车差速器多数是由锥齿轮副组成，通常是由2个行星直齿锥齿轮和2个半轴直齿锥齿轮组成。当汽车两侧车轮转速相同时，行星齿轮绕半轴轴线转动，称为公转；当两侧车轮阻力不同时，行星齿轮在公转的同时绕自身轴线转动，称为自转。行星齿轮自转时，2个半轴齿轮转速不同，此时整个差速器处于差速工况。当汽车直线行驶工况向差速工况过渡时，行星齿轮和半轴齿轮往往需要承受较大的载荷，传动过程中会出现大的滑动速度，如若齿面润滑不当，行星齿轮和半轴齿轮的接触表面会发生摩擦和磨损，严重时出现齿面胶合现象，导致齿面失效，特别对于半轴齿轮而言，齿面失效后，严重影响转向机构的寿命。众所周知，在汽车完成曲线行驶路段时，差速器的稳定运转直接关系整车的安全转向，当汽车在曲线行驶路段变化转向时，行星齿轮和半轴齿轮接触表面的速度发生明显的变化，2个表面的速度差必然发生变化，整个过程中的润滑状况比较复杂，因此对行星齿轮和半轴齿轮表面摩擦和磨损的管控至关重要。差速器锥齿轮并不总是经常处于啮合状态，当汽车转弯或左右轮行驶不同路程时，或一侧车轮打滑而滑转时，差速器行星齿轮才会发生相对运动。差速器锥齿轮常见的失效形式主要有齿轮齿面剥落、磨损、断裂、表面点蚀等，如果行星齿轮和半轴齿轮齿面润滑不当，齿面之间不易形成油膜，齿面直接接触会造成齿面的剥落。因此，研究差速器锥齿轮差速工况下的摩擦和磨损机制具有实际意义。

国内对汽车差速器锥齿轮的运动学及动力学分析研究较多，多从有限元的角度去研究锥齿轮的摩擦和磨损，且多从静态的角度去研究锥齿轮的运动特性。周新建等[2]阐述了差速器的传动原理，利用ADAMS建立了差速器齿轮结构的虚拟样机模型，并对该机构进行了2种工况下的仿真分析，得到传动齿轮的转速特性曲线及受力曲线，并通过对曲线分析了差速器的差速原理。张利鹏和祁炳楠[3]研究了差速器各部件之间的相互作用关系和半轴齿轮的差速机制，对其进行了受力分解和内摩擦力矩的计算，并对其转矩转速分配特性进行了建模。马骏[4]分析了汽车驱动轮和差速器行星齿轮的受力情况，阐述了对称式锥齿轮差速器实现差速的动力学原理。王良模等[5]运用现代方法分析了某汽车差速器齿轮静强度并预测其疲劳寿命，根据齿轮的对称性，建立了行星齿轮和半轴齿轮单齿的有限元模型。肖文颖和王书翰[6]对锥齿轮差速器的动力学进行了详细分析，根据差速器齿轮的力矩分配情况分析了差速器内摩擦对差速器锁紧系数的影响。付凯等人[7]提出了一种汽车差速器啮合效率的计算方法，选用直齿轮积分法啮合效率公式，将直齿锥齿轮等效为当量直齿圆柱齿轮，建立了一对定轴直齿锥齿轮的效率公式。冯海生等[8]研究了变工况对齿轮传动系统动特性影响，基于弹塑性接触理论，给出一种可以考虑变工况冲击、啮入冲击、节点冲击的齿轮接触碰撞力参数预估算法，并结合多体动力学软件建立柔性齿轮传动系统动力学模型。鲍培德等[9]基于弹性流体动力润滑理论，针对行星齿轮变速器内齿轮主动和太阳轮主动的2种工况，分别求出行星齿轮与太阳轮啮合以及与内齿轮啮合时，沿啮合线在啮合点的最小油膜厚度。李海鹏等[10]基于有限元动态仿真方法，建立差速器齿轮接触有限元模型，进行动态啮合仿真，研究了齿轮啮合时的应力分布情况。目前，国外相关学者对差速器的研究多集中于设计特征和运动分析[11-16]。本文作者基于多重网格法和多重网格积分法，对差速器锥齿轮建立时变弹性流体动力润滑模型，并针对差速工况，研究了行星齿轮和左右半轴齿轮的润滑特性。

1 差速器齿轮转矩及转速分配

研究对象为对称式圆锥齿轮差速器，差速器结构如图1所示，其半轴齿轮和行星齿轮主要参数如表1所示。

图1 差速器结构示意图

表1差速器锥齿轮相关参数

Table1Theparametersofdifferentialbevelgear

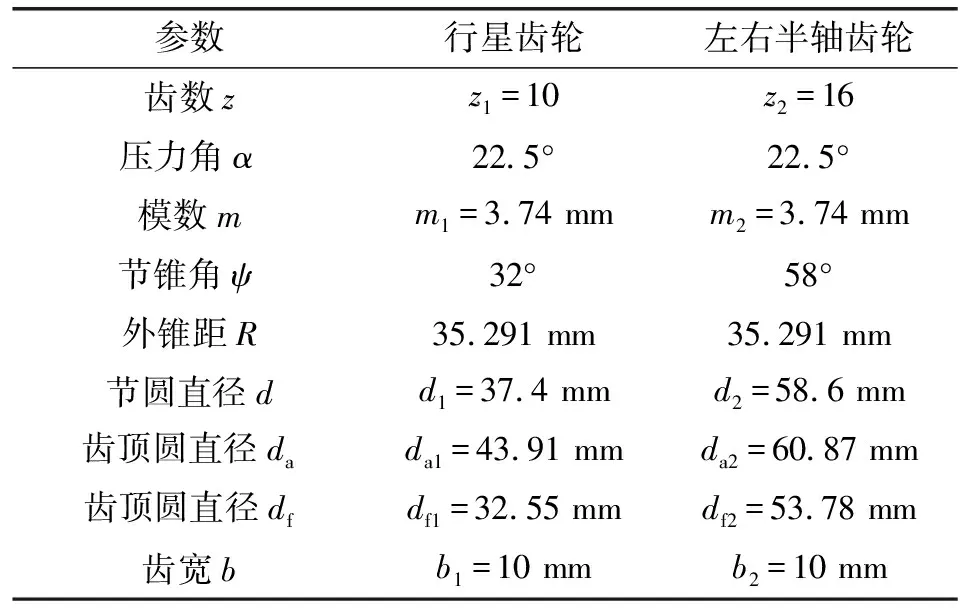
参数行星齿轮左右半轴齿轮齿数zz1=10 z2=16压力角α22.5°22.5°模数mm1=3.74 mm m2=3.74 mm节锥角ψ32°58°外锥距R35.291 mm35.291 mm节圆直径dd1=37.4 mm d2=58.6 mm齿顶圆直径dada1=43.91 mm da2=60.87 mm齿顶圆直径df df1=32.55 mm df2=53.78 mm齿宽bb1=10 mm b2=10 mm

差速器中壳体与齿轮的转矩关系如下：

T0=T1+T2

(1)

Tr=T2-T1

(2)

(3)

式中:T0是输入扭矩;T1和T2分别是左右半轴扭矩；Tr是内摩擦扭矩。

差速器中半轴齿轮、行星齿轮的转速关系为

n1+n2=2n0

(4)

(5)

式中：n1和n2分别是左右半轴齿轮的转速；n0是差速器壳体的转速；n3是行星齿轮的转速；r2和r3分别是半轴齿轮节圆半径和行星齿轮节圆半径。

通过差速器的转速和转矩特性方程，可以得到差速器转速和转矩分配情况[3]。图2所示是差速器左右半轴齿轮的转速曲线，图3所示是差速器输入扭矩曲线，图4所示是差速器转矩分配结果，图5所示是差速器转矩分配比。

图2 左右半轴齿轮转速随时间的变化

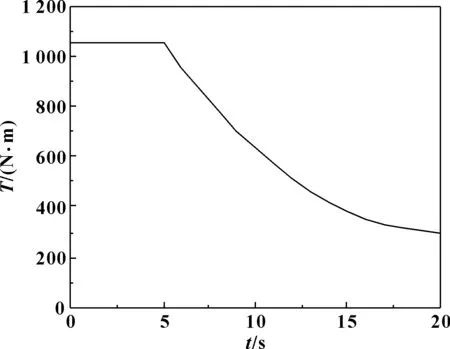
图3 输入扭矩随时间的变化

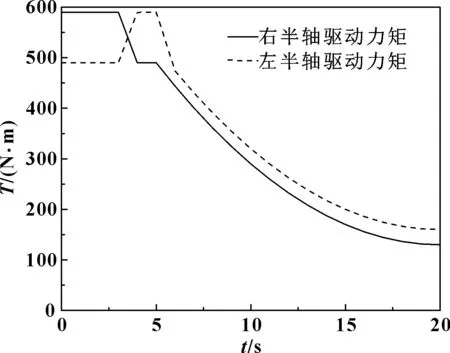
图4 差速器转矩分配结果随时间的变化

图5 差速器转矩分配比随时间的变化

由图2可知，起始阶段左半轴齿轮转速大于右半轴齿轮转速，在第3 s左右出现转速相同的情况，随后右半轴齿轮转速增长幅度大于左半轴齿轮转速增长幅度。由图3可知，差速器输入转矩在5 s之内保持不变，随后输入转矩逐渐减小。由图4可知，起始阶段分配给左半轴齿轮的驱动力矩小于右半轴齿轮的驱动力矩，随后左半轴齿轮的驱动力矩开始大于右半轴齿轮的驱动力矩。由图5可知，起始阶段差速器左右半轴齿轮驱动力矩分配系数略小，随后分配系数稳定在1.2附近。

2 数值分析

以汽车差速器为研究对象，结合实际工况，分离出汽车差速器行星齿轮和半轴齿轮，建立时变无限长线接触弹性流体动力润滑模型。等效模型图如图6所示。

表2给出了数值分析中涉及到的润滑剂和材料基本参数。

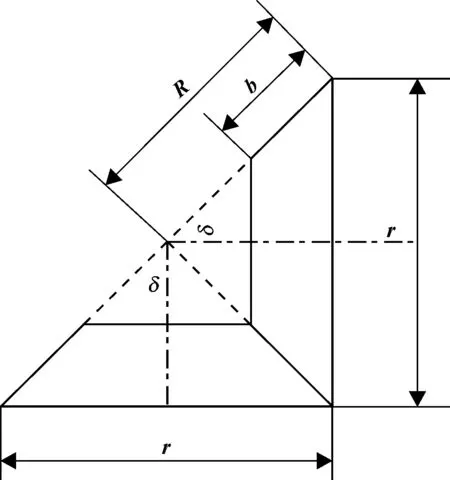
图6 直齿圆锥齿轮的接触等效图

表2基本参数

Table2Basicparameters

参数数值润滑油的环境黏度η0/(Pa·s)0.08黏压系数α/Pa-12.19×10-8齿轮的弹性模量E/GPa210泊松比μ0.3

2.1 Reynolds方程

(6)

式中：x为坐标变量；p为油膜压力(Pa)；h为油膜厚度(m)；ρ为润滑油密度(kg/m3)；η为润滑油黏度(Pa·s)；u为卷吸速度(m/s)。

2.2 膜厚方程

(7)

式中：h0为中心膜厚(m)；R为轮齿在啮合点处两齿廓的综合曲率半径(m)；E为两轮材料的综合弹性模量(GPa)。

2.3 黏压关系

η=η0exp{(lnη0+9.67)[(1+5.1×10-9p)z0-1]}

(8)

式中：η0为润滑剂环境黏度(Pa·s)；z0为Roelands黏压系数。

z0=α/[5.1×10-9(lnη0+9.67)]

(9)

2.4 密压关系

密压关系采用Dowson-Higginson公式

(10)

2.5 载荷方程

记w为单位长度上的载荷(N/m)，则压力应该满足载荷方程：

(11)

3 直线转曲线行驶差速工况下的润滑特性分析

如图7所示，差速器由直线行驶工况向差速工况过渡时，行星齿轮与左右半轴齿轮的转速和转矩均发生瞬时变化，差速工况下的行星齿轮与半轴齿轮进入啮合状态，两齿面开始发生相对滑动；相对直线行驶工况，行星齿轮需要承受较大的啮合力。由于行星齿轮需要同左右半轴齿轮同时参与啮合，故行星齿轮可以作为主要研究对象。图8所示是直线行驶工况和差速工况下行星齿轮与左半轴齿轮啮合时的中心膜厚分布。图9所示是2种不同工况下的滑滚比变化。图10所示是差速工况下行星齿轮分别与左右半轴齿轮啮合时的中心压力。图11所示是差速工况下行星齿轮分别与左右半轴齿轮啮合时的最小油膜厚度。

图7 直线行驶工况转差速工况

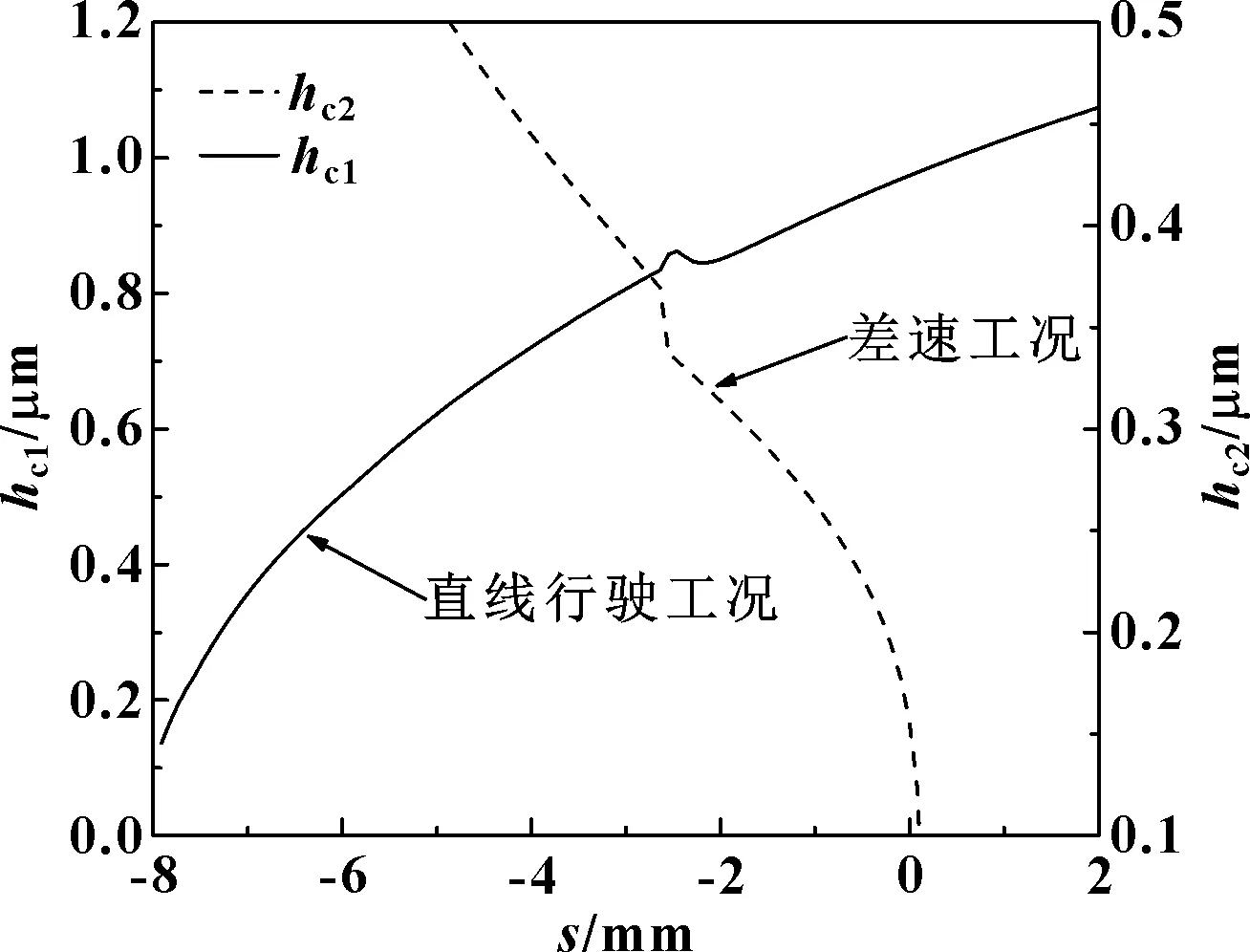
图8 直线行驶工况和差速工况下的中心膜厚分布

图9 直线行驶工况和差速工况下的滑滚比Δs变化

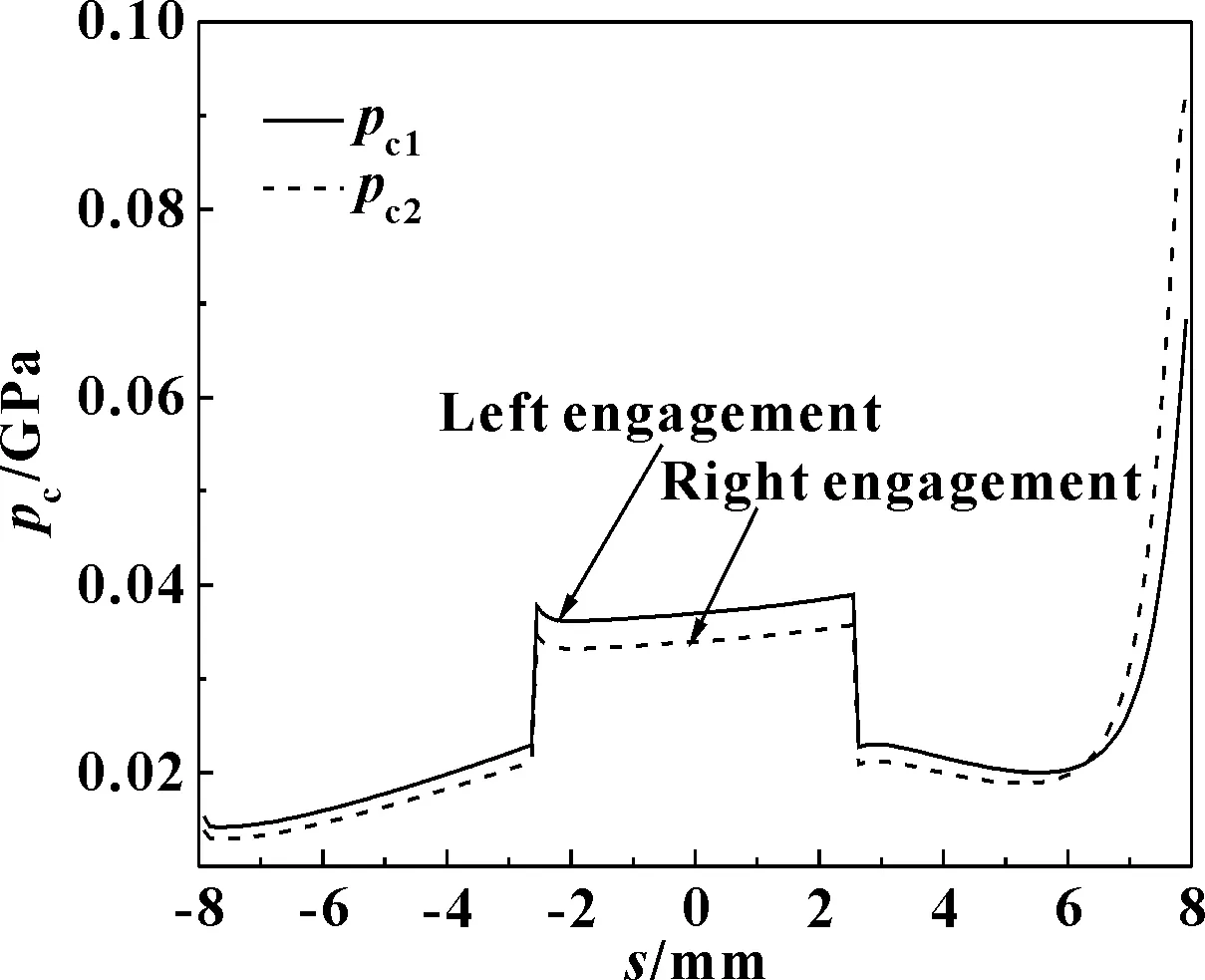
图10 差速工况下行星齿轮分别与左 右半轴齿轮啮合时的中心压力

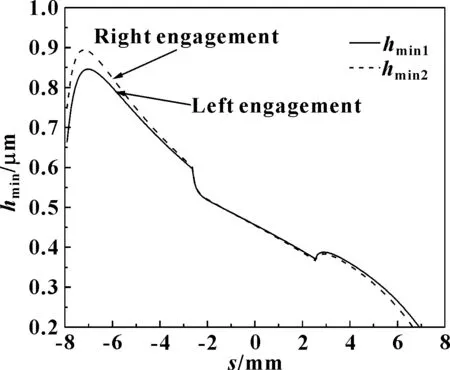
图11 差速工况下行星齿轮分别与左 右半轴齿轮啮合时的最小膜厚

图12所示是差速工况下行星齿轮分别与左右半轴齿轮啮合时的最大压力。图13所示是差速器行星齿轮的滑动速度。图14所示是左右半轴齿轮的滑动速度。图13和图14中的滑动速度是量纲一化滑动速度，该滑动速度用来表征行星齿轮和左右半轴齿轮的滑动趋势。

图12 差速工况下行星齿轮分别与左 右半轴齿轮啮合时的最大压力

图13 差速工况下行星齿轮分别与左 右半轴齿轮啮合时的滑动速度

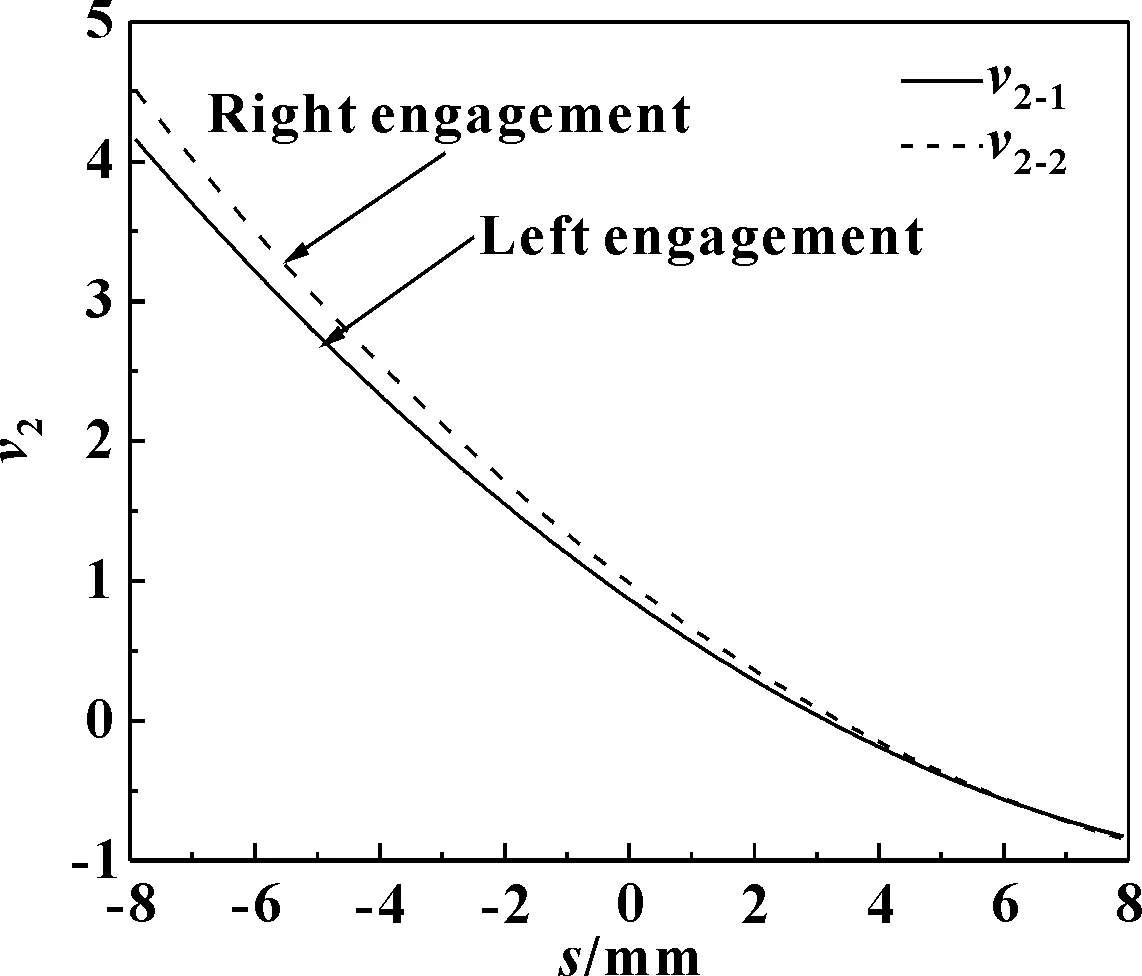
图14 差速工况下左右半轴齿轮的滑动速度

由图8可知，在直线行驶工况下，中心油膜厚度在整个啮合区间呈现出增加的趋势；在差速工况下，中心油膜厚度在整个啮合区间呈现出减小的趋势，且差速工况下的中心油膜厚度相比直线行驶工况下的中心油膜厚度较小。由图9可知，差速工况下的滑滚比相对直线行驶工况下的滑滚比较大，通过2种工况滑滚比对比可知，差速工况下行星齿轮与半轴齿轮的齿面滑动相对较大。 由图10可知，行星齿轮与左右半轴齿轮啮合的中心油膜压力在整个啮合区间有所不同，在啮入区间，行星齿轮与左半轴齿轮啮合时的中心油膜压力大于行星齿轮与右半轴齿轮啮合时的中心油膜压力，越过啮入区间后，行星齿轮与左右半轴齿轮啮合时的中心油膜压力先减小后增加。由图11可知，行星齿轮同右半轴齿轮在啮入区间的最小油膜厚度大于行星齿轮与左半轴齿轮在啮入区间的最小油膜厚度。

图13和图14分别反映的是行星齿轮和左右半轴齿轮的速度变化，由图13可知，行星齿轮同左右半轴齿轮啮合时的齿面滑动速度均为先增大后减小的趋势。由图14可知，左右半轴齿轮齿面滑动速度在差速工况下逐渐较小，由差速器转速方程可知，差速器左右半轴齿轮的转速变化同行星齿轮的转速变化无关。

在差速工况下，行星齿轮发生自转，同时与左右半轴齿轮参与啮合，行星齿轮齿面同左右半轴齿轮齿面发生相对滑动，行星齿轮和半轴齿轮的转速发生变化，当差速器由直线行驶工况转向差速工况时，行星齿轮的转速发生瞬时变化，左右半轴齿轮的转速变化不同，右半轴齿轮的转速大于左半轴齿轮的转速，其转矩也随之发生变化。

4 曲线行驶路段差速变工况下的润滑特性分析

曲线行驶路段差速变工况分为2个部分，其一是直线行驶工况过渡到左转弯工况，其二是左转弯工况过渡到右转弯工况。图15所示是曲线行驶路段变工况简图。

图15 曲线行驶路段变工况

图16所示是2个工况下同左半轴齿轮啮合的行星齿轮齿面量纲一化滑动速度，图17所示是2个工况下行星齿轮与左半轴齿轮啮合时的最小油膜厚度变化。图18所示是2个工况下行星齿轮与左半轴齿轮啮合时的最大压力变化。其中第一个工况是左转弯工况，第二个工况是右转弯工况。

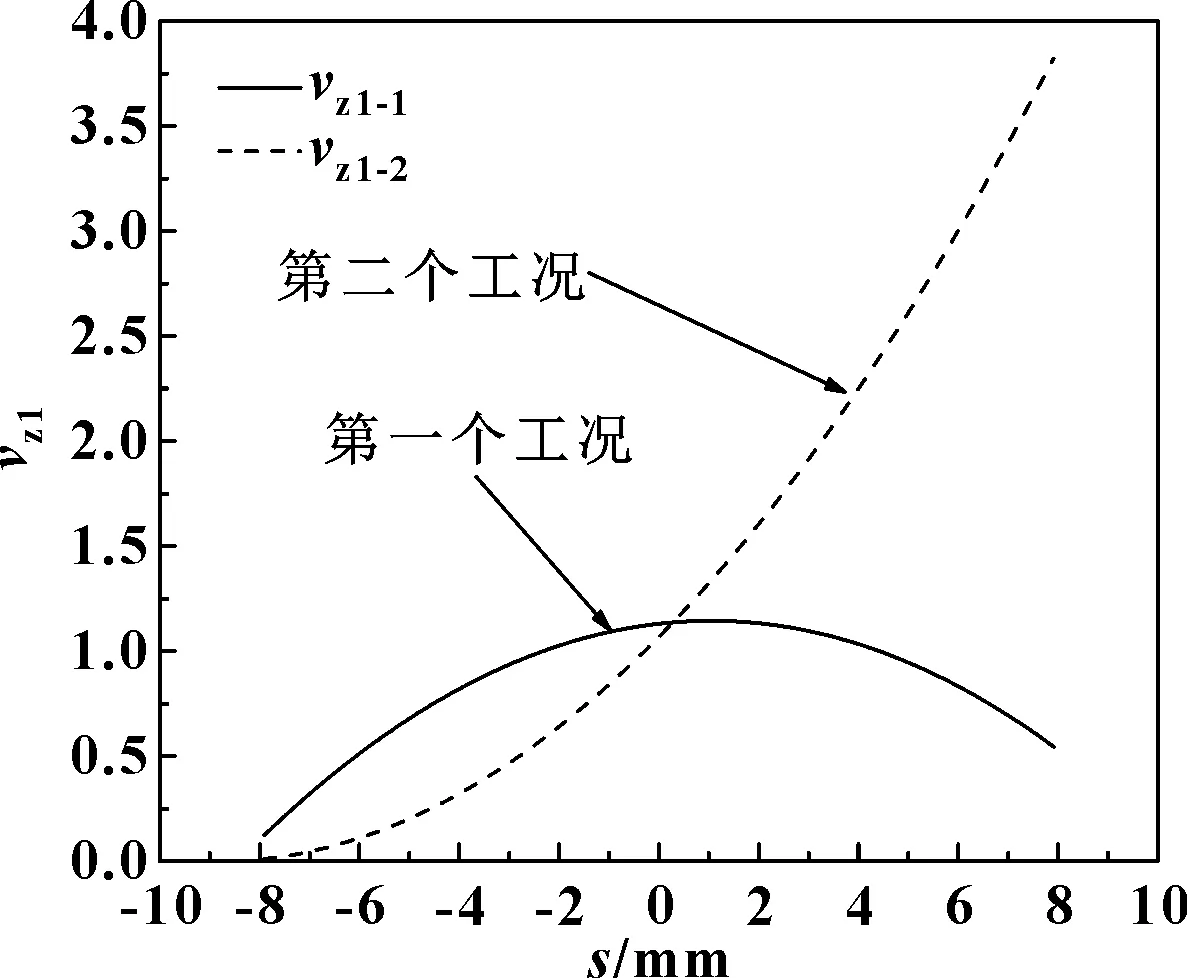
图16 变工况下行星齿轮的滑动速度

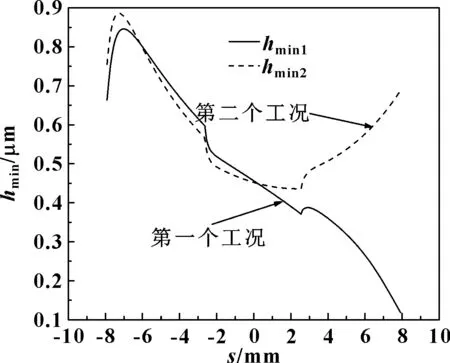
图17 变工况下行星齿轮与左半轴齿轮啮合时的最小油膜厚度

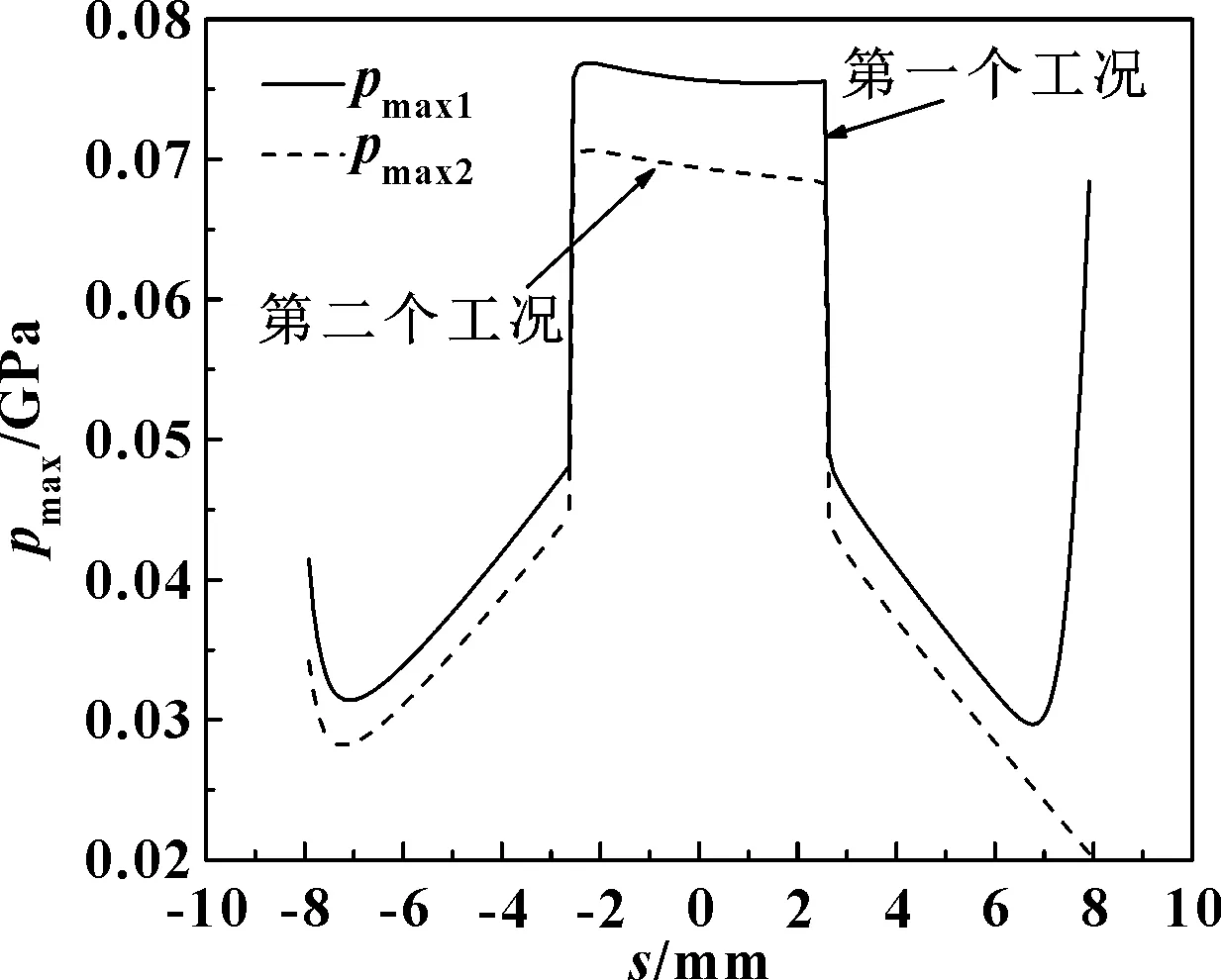
图18 变工况下行星齿轮与左半轴齿轮啮合时的最大压力

由图16可知，在开始进入啮入区间时，第一个工况下的行星齿轮齿面滑动速度比第二个工况下的行星齿轮齿面滑动速度大，伴随着行星齿轮与左半轴齿轮的啮合，第一个工况下的行星齿轮齿面滑动速度逐渐减小，而第二个工况下的行星齿轮齿面滑动速度逐渐增大。由图17可知，第二个工况下行星齿轮与左半轴齿轮啮合的最小油膜厚度，大于第一个工况下行星齿轮与左半轴齿轮啮合的最小油膜厚度。由图18可知，第二个工况下行星齿轮与左半轴齿轮啮合的最大油膜压力，小于第一个工况下行星齿轮与左半轴齿轮啮合的最大油膜压力。

5 结论

(1)当差速器由直线行驶工况进入差速工况时，行星齿轮同半轴齿轮啮合时的中心膜厚减小，行星齿轮同半轴齿轮啮合时的滑滚比增大，两齿面发生较大的相对滑动。

(2)差速工况时行星齿轮同左半轴齿轮啮合时的最小油膜厚度和最大油膜压力，明显有别于行星齿轮同右半轴齿轮啮合时的最小油膜厚度和最大油膜压力，由于左转弯工况下的左半轴齿轮转速小于右半轴齿轮转速，而速度对最小油膜厚度的影响较大，所以在整个啮合区间行星齿轮同左右半轴齿轮的润滑状况有所不同。

(3)差速变工况下的左右半轴齿轮的转速发生变化，当由第一个工况转入第二个工况时，行星齿轮的转速逐渐增大，此时行星齿轮与左半轴齿轮的相对滑动加剧，行星齿轮与左半轴齿轮啮合时的最小油膜厚度瞬时增大。