单层稳恒电流斗篷

赵艳艳，曾伦武

（南京农业大学工学院，江苏南京210031）

近几年来，隐身斗篷吸引了科研工作者的广泛关注，根据Pendry等的先锋工作[1-4]，科研工作者理论设计和实验验证了各种电磁波斗篷[5-11]、声波斗篷[12-14]、物质波斗篷[15]、质量扩散斗篷[16]、热扩散斗篷[17-20]、磁斗篷[21-23]、直流电斗篷[24]。首次实验证明隐身斗篷是利用简化参数的超材料[5]。简化参数的超材料斗篷拥有理想斗篷的性质，但存在有限的散射。用自然界存在的材料制造完美的电磁斗篷是相当困难的，因为完美斗篷需要各项异性材料。但完美的直流电斗篷很容易用自然界存在的材料制造，Yang等利用电阻网络设计了各项异性的电导并且实验证明了直流电斗篷[24]，他们的工作表明直流电斗篷能够引导电流绕过斗篷区域。Gömöry等利用超导体和铁磁质材料实验证明了磁斗篷[22]，磁斗篷不需要各项异性的超材料归因于超导体的零磁导率。根据相似的方法，Zeng设计了双层电流斗篷[25]，双层稳态电流斗篷不需要各项异性的超材料，归因于绝缘体的零电导率。Han等也设计了同样的稳恒电流斗篷[26]。根据热导方程和电导方程的相似性，Han和Xu等各自独立地实验证明了双层热扩散斗篷[19,20]，双层热扩散斗篷能够屏蔽热通量，这种热屏蔽是暂时的热扩散保护，在稳态情况下，斗篷区域最终达到同样的温度。本文中，依据设计双层斗篷的思想，设计了单层稳恒电流斗篷，计算和模拟结果表明，单层导体能够斗篷稳恒电流。

1 单层稳恒电流斗篷

时间依赖的电导方程为∇·(σ∇φ)=∂ρ/∂t,式中ρ是电荷密度，φ是电势。在稳恒电流情况下，电荷密度不随时间变化，那么∂ρ/∂t=0。当媒质为各向同性均匀电导时，电导方程变为拉普拉斯方程如图1所示，无限长的双层（先假设为双层，后面证明只需要单层就可以斗篷电流）空心圆柱内外半径分别为b和a,c和b，当稳恒电压加于导体两端时（即外电场E0施加于导体），在圆柱坐标系(r,θ,z)中，解拉普拉斯方程，得到4个区域的电势分别为[22]

式中φe1、φe2、φe3、φe4分别为4个区域的电势，A、B、C、D、E、F为待定系数。

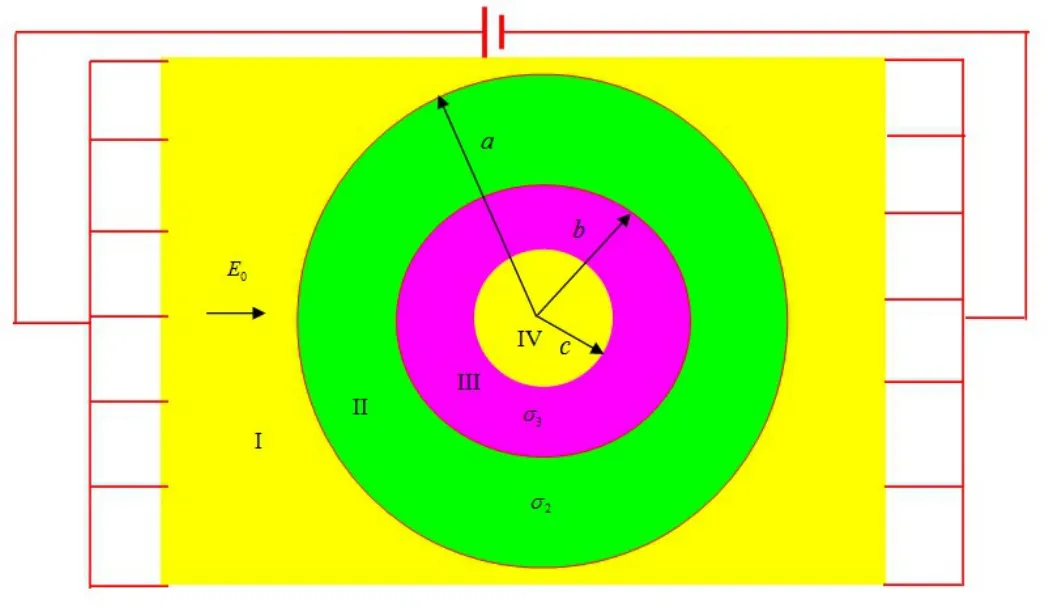
图1 背景媒质和圆柱斗篷截面。I：背景媒质；II：空心圆柱导体；III：假想的空气圆柱；IV：斗篷区域

根据欧姆定律的微分形式可知，电流密度和电势的关系为J=-σ∇φ，其中是电流密度，σ是电导率，4个区域的电流密度分别为

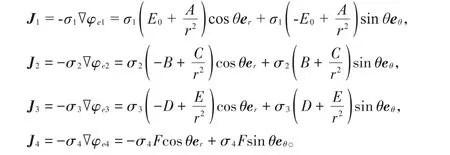
式中er是法线方向的单位矢量，eθ是切线方向的单位矢量。利用电场切线方向（或者电势）连续和电流密度法线方向连续的边界条件得到

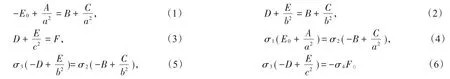
我们感兴趣的是系数A和F，也就是说，只考虑区域I和区域IV的电流或电流密度。当A=0时，电流密度在区域I保持σ1E0不变；当F=0时，电流密度在区域IV消失，也就是电流密度在区域IV被斗篷。由（3）式和（6）式可知，当F=0时，σ3=0。令A=0，F=0，σ3=0，解方程（1）～（6）得

（7）式为斗篷材料参数和尺寸参数的关系，也是斗篷成立条件。图2(a)绘出了σ1一定时（σ1=3.45×107S/m），a b与σ2的关系；图2(b)绘出了σ2一定时（σ2=5.9×107S/m），a b与σ1的关系。 在（7）式中，如果取σ1=3.45×107S/m（铝），σ2=5.9×107S/m（铜），则a/b≈1.95。因为σ3=0的材料在自然界不存在，用空气（电导率为10-14S/m）近似代替σ3，σ3=10-14S/m→0，计算和模拟表明，斗篷的性能和半径c无关。也就是说，c可以等于b，当c=b时，区域III和区域IV都为空气，这样，斗篷就变成了单层斗篷。应该指出，由于选取了σ3=10-14S/m→0，这就决定了斗篷是一个近似斗篷。斗篷的性能与σ3的大小密切相关，当σ3=0时，实现完美斗篷。图3绘出了当σ3=10-14S/m时外加电场和斗篷区域电场的关系。当外电场E0=104V/m，斗篷区域的匀强电场为E=3.201 5×10-10V/m；当外电场E0=105V/m，斗篷区域的匀强电场为E=3.201 5×10-9V/m。这种近似电流斗篷已经很接近完美电流斗篷了。应该指出：电流斗篷和电流屏蔽是不同的，虽然斗篷和屏蔽时中心区域都没有电流，在斗篷情况下，导体圆柱外部电流密度均匀，在屏蔽情况下导体圆柱外部电流密度可以不均匀。

图2 半径比率a b与电导率σ的关系。（a）σ1定值；（b）σ2定值

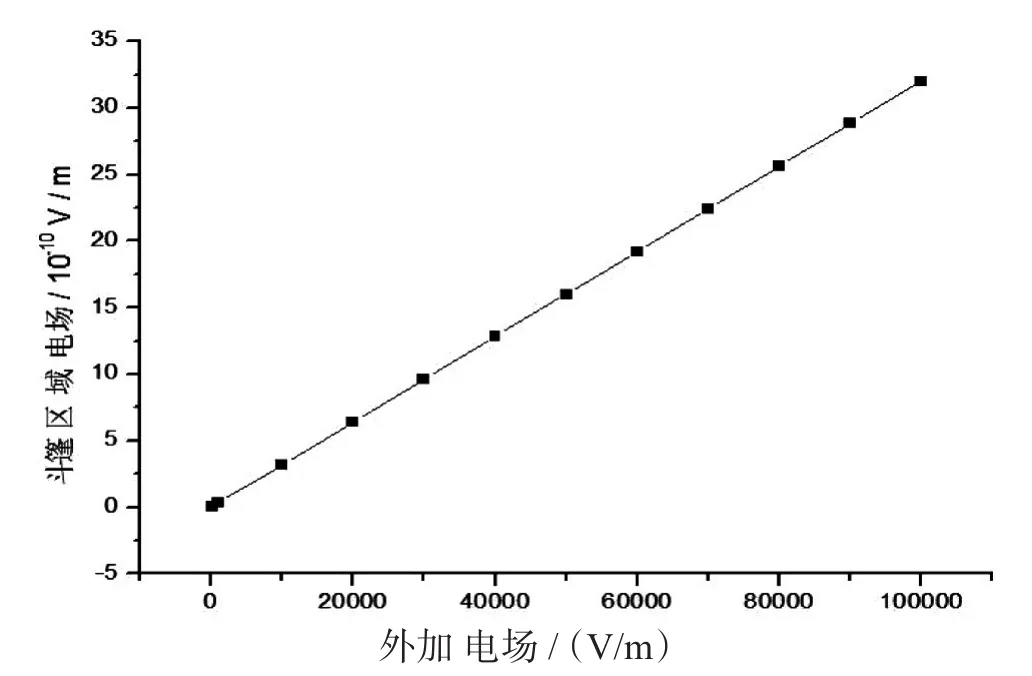
图3 外加电场和斗篷区域电场的关系

2 模拟电流斗篷

利用COMSOL Multiphysics有限元软件，模拟导体圆柱的电流屏蔽和斗篷。图4(a)表示没有屏蔽时电流密度线的分布，背景媒质的电导率和导体圆柱的电导率均为3.45×107S/m，电流密度线平行。图4(b)表示单层空心圆柱电流屏蔽图，其内外半径分别为0.5 cm和1.95 cm，空心圆柱电导率为102S/m。背景媒质和中心的电导率均为3.45×107S/m，电流密度线不平行。图4(c)为双层空心圆柱电流屏蔽，按照方程（7），取内空心圆柱内外半径分别为0.5 cm和1.0 cm，外空心圆柱内外半径分别为1.0 cm和1.95 cm，内空心圆柱电导率为10-14S/m，外层空心圆柱电导率为5.9×107S/m，背景媒质电导率为3.45×107S/m，斗篷区域电导率为10-14S/m，在外圆电流密度线平行，并且电流密度线不能进入内圆。在图4(c)中，斗篷区域电导率为10-14S/m，当斗篷区域和内层都为空气时，斗篷变成了单层斗篷。进一步研究表明，内半径c在不超过b的情况下取任意值，斗篷的性能不变。图5绘出了c为不同值时的斗篷效果，在图5(a)中，c=0.6 cm，区域III和区域IV均为空气；在图5(b)中，c=0.7 cm，区域III和区域IV均为空气；在图5c中，c=0.8 cm，区域III和区域IV均为空气；在图5(d)中，c=0.9 cm，区域III和区域IV均为空气；在图5(e)中，c=b=1.0 cm，区域III和区域IV变成了同一区域，均为空气。图5中其他参数和图4c相同。在图5(e)中，c=b=1.0 cm，此时的斗篷实质上变成了单层斗篷，也就是背景媒质为铝，单层导体空心圆柱材料为铜，内部为空气。

图5 内半径c为不同值时的斗篷效果，区域III和区域IV为空气

3 结论

利用导体和绝缘体材料，设计了双层电流斗篷，当绝缘体为空气时，双层斗篷变成了单层斗篷。理论计算和数值模拟表明：单层导体能斗篷电流并且不改变电流分布。斗篷的条件不仅由材料的电导率决定，而且由材料的几何参数决定，这一结果很容易实验证明。