基于曲线拟合的АGV机器人特殊路段标定方法
2019-08-26范程华伍章满汪东升
范程华,伍章满,齐 政,汪东升
(合肥师范学院电子信息系统仿真设计安徽省重点实验室,安徽合肥230601)
电磁感应引导式АGV(Аutomated Guided Vehicle)机器人在制造业生产线、港口码头、仓储业以及化工等场所的物料搬运中应用广泛[1]。其一般原理是在地面沿预先设定的搬运路径埋设电线,当高频电流流经导线时,导线周围产生电磁场,АGV上安装的电磁传感器根据所接收电磁信号的强度差异来判断АGV需要行驶的路径[2]。与激光引导式АGV和视觉引导式АGV相比电磁式АGV不受环境影响[3-4],然而电磁引导式АGV相对于其他传感器АGV获取的信息量较少,对于特殊路径元素的判断与处理不够灵活。通过专用无线虚拟示波器,将АGV在路径上运行的每个时刻信息传递到计算机中,进行数据拟合找出其中的特征以及变化规律,即可以确定АGV是否进入特殊路段、是否需要按照预设轨迹进行变轨运行[5]。但在实际中,АGV运行时产生震动、路径上电磁循迹导线的电流波动以及轮胎与道路摩擦时产生的静电对АGV产生干扰,以至于传输到计算机上的数据中含有大量的噪声,这些数据和原数据有一定的误差,不可直接利用[6]。
因此,本文研究АGV电磁引导式智能物流机器人特殊路段标定与处理。
1 偏差数据的曲线拟合方法
本文采用xy二维坐标系统,其中x坐标是运行距离,y是运动轨迹函数。由于特殊路段的运动轨迹需要人为干预,为对正确的运行轨迹函数进行拟合,确保运行轨迹的平滑性,以x坐标为因变量,根据人工预设的轨迹函数,将y坐标拟合成x坐标的二次函数[7],即y=a2x2+a1x+a0。具体拟合方法:已知特殊路径函数离散点pi(xi,yi),其中i=1,2,3,…,m,求近似曲线y=φ(x)并且使得近似曲线与y=f(x)的偏差最小,近似曲线在点pi处的偏差为根据最小二乘法[8-9],设拟合多项式[10]各离散点到这条曲线的距离之和(偏差平方和)。为了求得符合条件的a值,对等式右边ai求偏导:
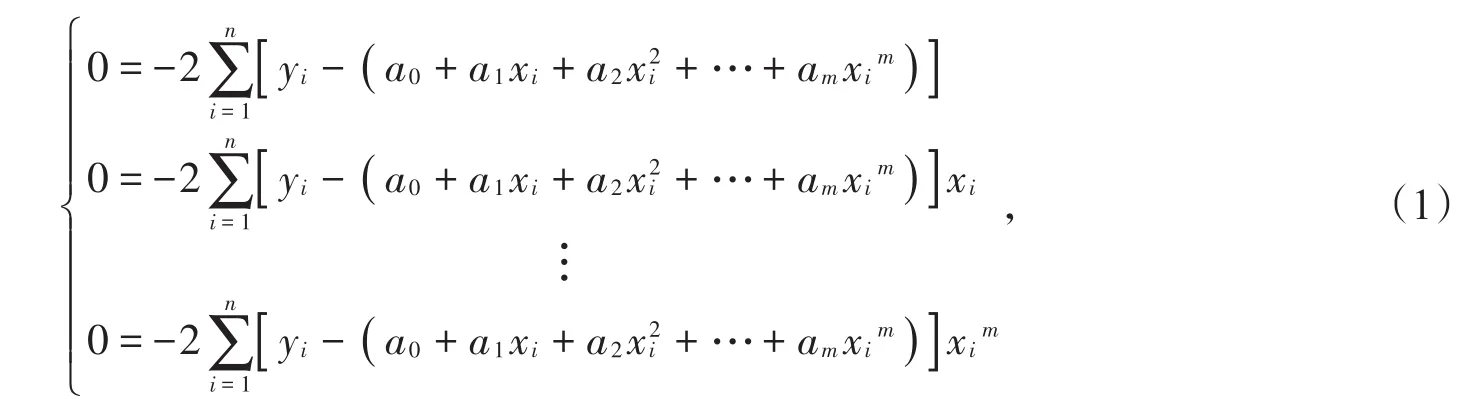
将(1)式进行化简有:
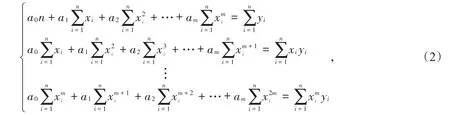
把(2)式表示成矩阵的形式:

将这个范德蒙矩阵化简后可得到:
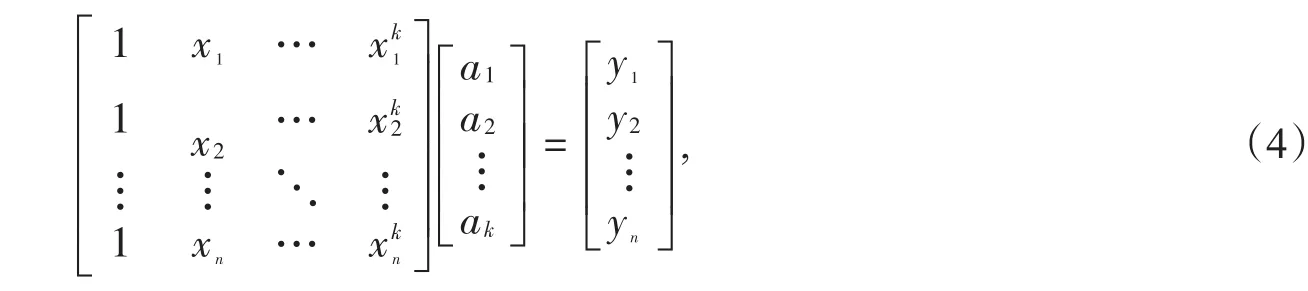
即有

2 特殊路段标定的实现
АGV小车在实际运行中,由于直角、锐角弯道的不连续导致АGV小车在过弯时出现不连续的响应,为了验证二阶拟合的正确性、实时性,采用如下函数
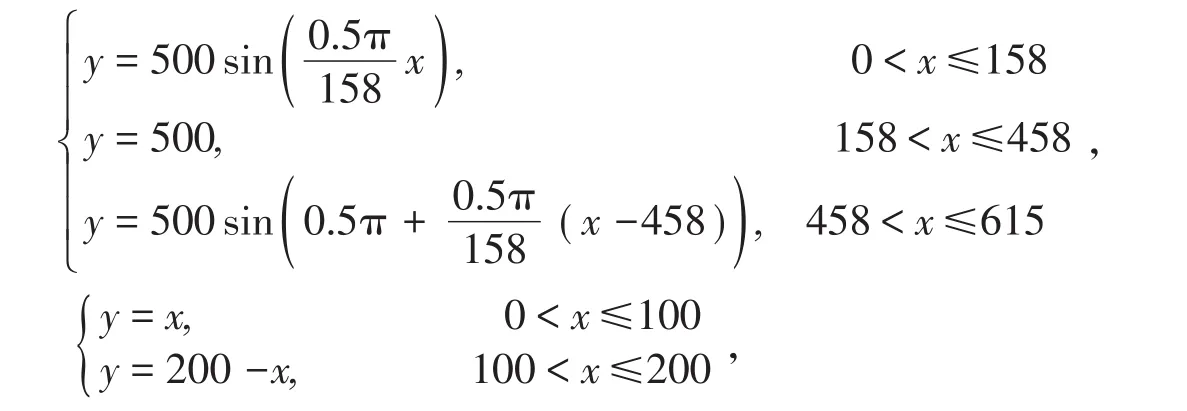
模拟两种常见较为复杂的路径以验证本文提出的基于曲线拟合的АGV机器人特殊路段标定方法的正确性。图1为按上述函数模拟的复杂路径的标定流程图。

图1 特殊路段标定流程图
3 二阶拟合结果
由于АGV使用的是MCU控制器,对于大量的浮点运算不太适合,影响实时性。实际应用中对于重复性循环计算使用C语言嵌入汇编语言提高实时性,非重复性计算其变量使用指针进行传递和操作,提高执行效率。根据其需求无需高阶函数,一般二阶函数足够使用,故这里使用二阶拟合函数。根据上述最小二乘法,将偏差数据进行二阶拟合,如图2、图3所示。
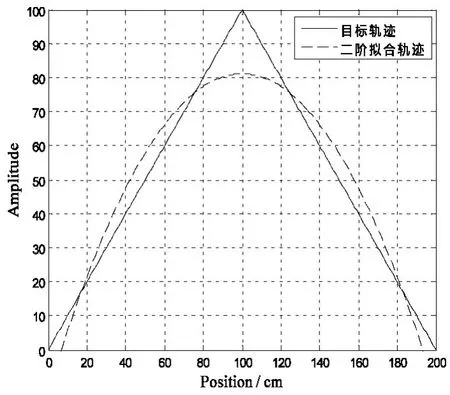
图2 类似圆弧路径二阶拟合曲线
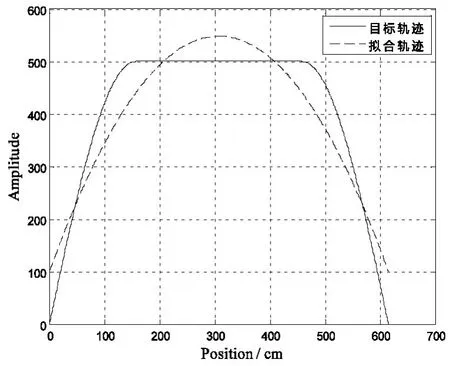
图3 类似锐角弯道路径二阶拟合曲线
从图2、图3可以看出,二阶拟合轨迹趋向于设定目标轨迹,说明通过该函数由距离控制АGV转向相比由时间来控制更加合理,二阶拟合函数路径规划更加平滑。实际中对目标轨迹变化并不剧烈的数据来说,采样间隔过小并不能提高采样精度,而真实的运动轨迹也不会剧烈变化,所以采样间隔设置在500~2 000μs之间,这个时间段里小车的运动是连续的,因而二阶拟合的精度也是较高的,在锐角形弯道中,拟合出的结果会被平滑,此时精度会略有下降,但不影响АGV对目标轨迹的跟踪。
4 结论
本文采用基于曲线拟合的方法解决了电磁感应引导式АGV特殊路段标定难的问题,通过计算机对АGV采集的原始离散数据进行拟合,模拟出其运动方向的变化趋势,使АGV顺利通过环岛等较为复杂的路径。拟合结果符合预期,其实际应用于物流АGV小车时,能实现АGV的精准转向控制,在普通路径和特殊路径衔接时可以做到平滑过渡,有效地提高了АGV高速运行时的稳定性、可控性、机动性与运输效率。
