Wiener指数，Hyper-Wiener指数，Harary指数与图的β-亏损性

夏祥伟，叶淼林

（安庆师范大学数学与计算科学学院，安徽安庆246133）

本文所涉及的图均为简单无向连通图。设G=( )V,E是n阶m条边的简单连通图，其顶点集为V=，边集为E，其中的顶点v的度d()v是指G中与v关联的边的数目，用表示G的顶点的最小度。若在G中顶点u和v是连通的，则u和v之间的距离d( )u,v是G中最短( )u,v路的长。每一对不同的顶点都有一条边相连的简单图称为完全图，n个顶点的完全图记为Kn。G的补图Gˉ是指和G有相同顶点集V的一个图，在Gˉ中两个顶点相邻当且仅当它们在G中不相邻。设和是两个顶点不相交的图，用表示它们的并图；用表示它们的联图，即在G1⋃G2中添加由G1中每个顶点到G2中每个顶点的边所得的图。图G的亏损数是指G中所有顶点个数与它的最大匹配中顶点个数之差，如果def( )G ≤β，则称图G是β-亏损的。表示

Wiener指数是在研究有机化合物的物理化学性质时经常使用的经典拓扑指数，定义为[1]

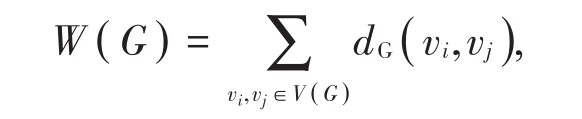
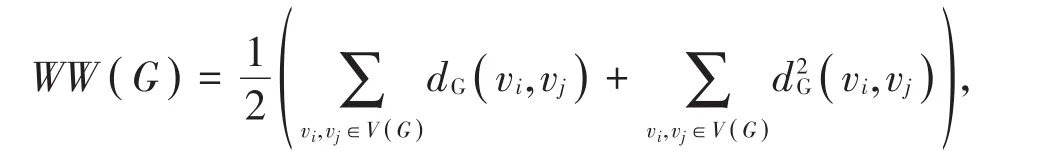
图G的Harary指数是指该图中所有顶点对之间的距离倒数之和[4-5]，即H记，则有H

决定一个给定的图是否是亏损的，是图论中的一类NP问题。近年来，各国学者对拓扑指数和图亏损性的研究不断深入，得到了很多充分或必要条件。Petrosyan等对图的亏损性进行研究，得到一些有关完全图K2n+1和def( G )界的结论[6]；文献[7-11]通过研究部分拓扑指数讨论了图的哈密尔顿性；任丽芳等利用图的Wiener指数、hyper-Wiener指数和Harary指数，分别给出了具有最小度条件的连通图是哈密顿-连通的以及从任一点出发都是可迹的充分条件[12]。受上述文献的启发，在文献[13]的相关条件基础上，利用图的Wiener指数、hyper-Wiener指数和Harary指数，给出了具有最小度条件的连通图是β-亏损的几个充分条件。值得注意的是，补图的β-亏损同样也具有一定的研究价值。下面先介绍相关引理。