一种大规模MIMO低精度量化检测算法

张永棠

(1.广东东软学院计算机学院, 广东 佛山 528225;2.南昌工程学院江西省协同感知与先进计算技术研究所, 南昌 330003)

引 言

近几年来，基站端配置大量天线的大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)系统是5G移动通信系统的热点[1]。由于大规模MIMO系统中基站配置天线数量非常大，若采用高精度的模数转换器，基站的成本将变得难以承受。因此考虑硬件成本的开销，在接收端采用低精度量化成为可能的解决办法。将低精度量化技术与大规模MIMO技术相结合，得到了业界研究者认可。文献[2-3]提出了一种高精度与低精度混合的ADC架构，达到相对可观的系统性能。文献[4]设计了一个低精度量化的MIMO系统，在信道容量上得到了很好的优化效果，但是系统的误比特率明显增加。

由于低精度量化器的使用会导致传统线性检测算法(如MMSE)的性能有所下降，出现更大的误码，同时还需要很长的导频序列去获取信道状态信息(Channel State Information, CSI)[2,5]，于是越来越多的学者考虑新的检测算法。近似消息解量化算法(Message Passing De-quantization，MPDQ)是基于广义近似消息传递算法(Generalized Approximate Message Passing，GAMP)的一种改进型算法[6]，作为一种新的低精度解量化算法，在量化信号的重建中性能优异。文献[7]在特定的CSI条件下，采用1-bit量化的大规模毫米波通信系统推导信道容量。文献[8]研究了在高信噪比或无噪声的环境下，1-bit压缩感知的重构算法。

由于上述特定环境在实际应用中是比较容易实现的，本文以低精度ADC接收机为基础，搭建了一个大规模MIMO系统模型，研究一种大规模MIMO低精度量化检测算法，分析MPDQ在1-bit量化系统中的性能，并将其推广到n-bit量化系统，推导MPDQ算法在n-bit量化系统中的迭代计算公式。

1 系统模型

在大规模MIMO低精度量化系统中，接收天线后面连接有两个低精度模数转换器(Analog-to-Digital Converter, ADC)，分别对天线接收数据的实部和虚部进行量化，系统模型如图1所示。

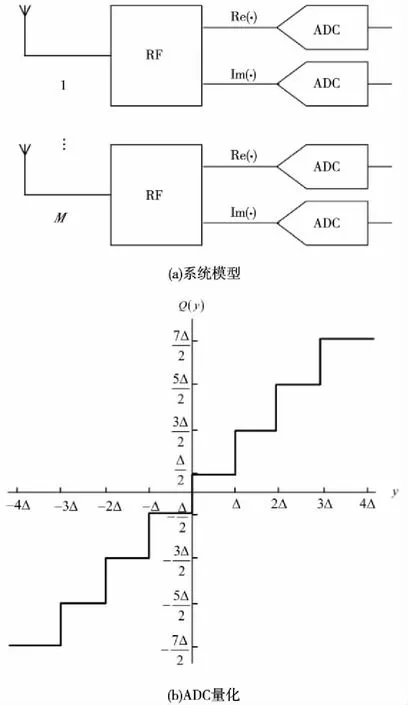
图1 大规模MIMO低精度量化系统模型

考虑到大规模MIMO系统场景，假设基站天线数为M，每一根天线资源服务的用户数为U，且MU>1。则基站端接收到的量化前的信号可以表示为：

y=Hx+n

(1)

其中，H∈M×U表示基站端与用户端的信道矩阵，是简单的平坦衰落信道。为第u个用户发送符号，其协方差矩阵E[xxT]=pIU，假设所有用户的发送功率p是相等的。这里采用简单的QPSK调制方式，n为循环高斯复随机变量，即满足n～CN(0,1),y为基站接收向量。

经过ADC量化后，输出的信号r可以表示为：

r=Q(y)=Q(Hx+n)

(2)

其中，Q(·)为量化函数[9], 大规模MIMO系统中多用户检测目的就是已知n的分布和H，从r中重建发送信号x。

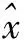
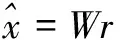
(3)

2 低精度量化检测算法

随着压缩感知理论的提出，置信传播(Belief Propagation,BP)[10]被应用到通信系统的信号检测中。BP算法需要高维积分，所以在实际计算中很复杂。BP算法可以通过泰勒展开简化为 GAMP算法应用到量化系统中，简化成MPDQ算法[11-12]。MPDQ通过矩阵的乘法和加法以及标量的非线性处理来代替高维积分，减少了计算复杂度，迭代过程如算法1所示。

算法1 MPDQ算法迭代过程

(8)

其中，R和I分别表示数据的实部和虚部，则式(6)和(7)可以表示为：

(9)

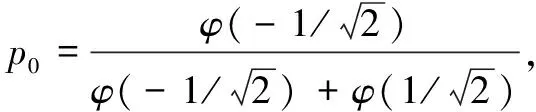
(10)

(11)

最终问题的难点就在如何求任意量化区间的

经过推导可得：

(12)

3 优化问题求解

由系统模型可知，每根天线都配备了一对ADC，分别用于实部和虚部量化。则ADC的功耗可以表示为：

PADC,m=2α·2bm

(13)

其中，bm为量化精度；α为一个常数，用于表示ADC设计相关的参数。

根据式(13)可以得出基站的总功耗为：

(14)

其中，Pc为基站的其他功耗，在这里是为一个常数。

由于量化精度矢量b={b1,b2,…bm}会同时影响速率和功耗，因此量化精度不是越高越好，有必要对ADC的精度进行优化，以求解满足速率最优时的b*。优化问题求解可描述为：

(15)

其中，Pmax表示最大总功耗，R表示系统速率之和。

4 仿真结果与分析

仿真参数设置：调制方式为QPSK[13]，采用Rayleigh衰落信道，用户的发送功率为10 dB，ADC精度分别设为1～5 bit。基站天线数M和用户数U设为128×16和128×64。功耗常数α=10-4W，Pc=0.02 W[14]。量化器为均匀量化，其参数见表1。

表1 均匀量化器参数设置

首先，对大规模MIMO 1-bit系统中多用户检测算法MMSE和MPDQ进行仿真，如图2～图3所示。

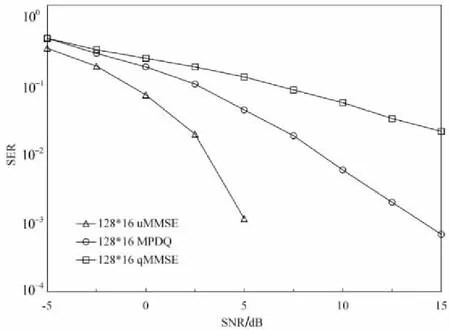
图2 128×16 1-bit系统误符号率曲线

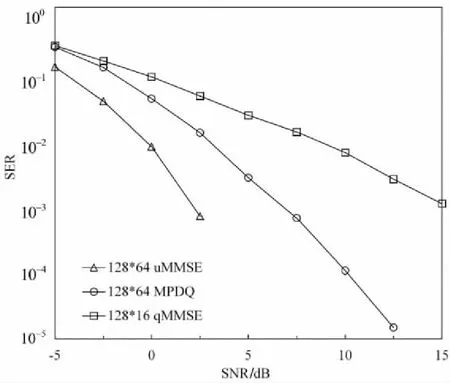
图3 128×64 1-bit系统误符号率曲线

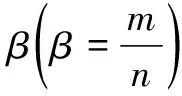
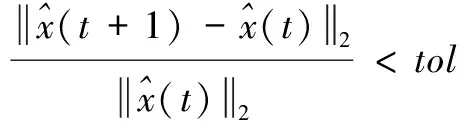
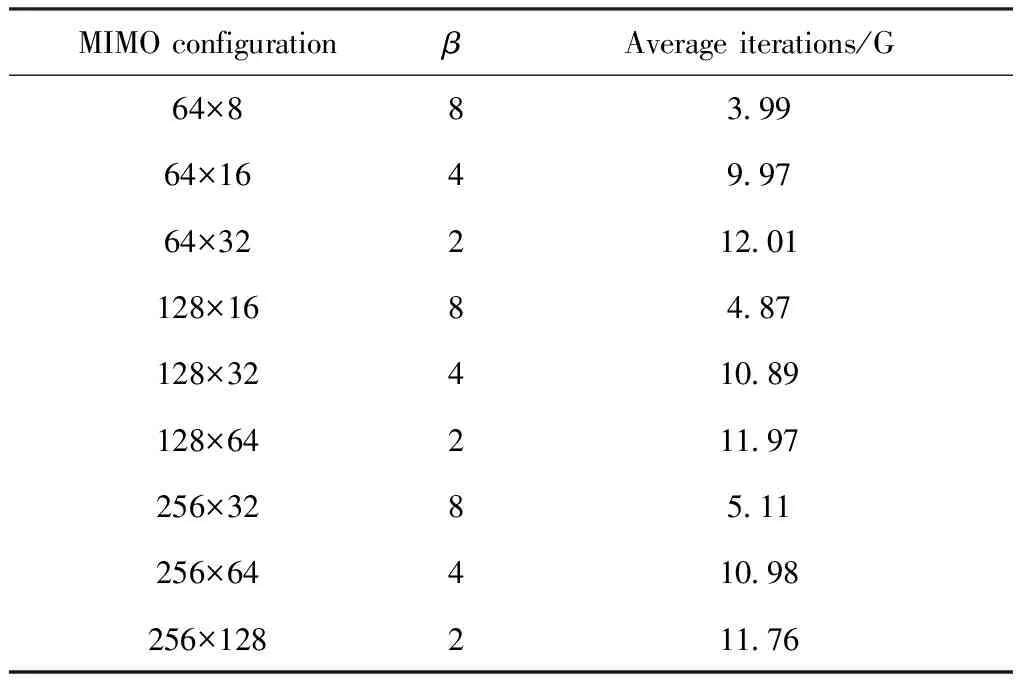
表2 1-bit系统MPDQ检测算法平均迭代次数

图 4 给出了n-bit MPDQ算法误码性能。由图4可以看出，随着量化器精度的提高，误码率性能更好，其中3-bit量化误码性能与无限精度时相差很小。综合考虑性能和成本因素，3-bit量化可认为是一种理想的方案。

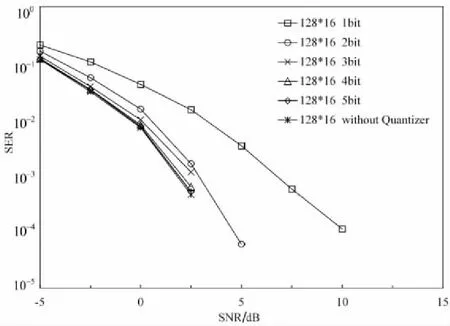
图4 n-bit MPDQ检测算法性能

其次，将文章提出的MPDQ优化模型与已有Bussgang模型[2,18]进行对比分析，两种模型在不同天线数量下的和速率(容量)如图5所示。由图5可见，本文提出的模型优于Bussgang模型，尤其是在1-bit低精度量化时，随着天线数量的增加优势更加明显。

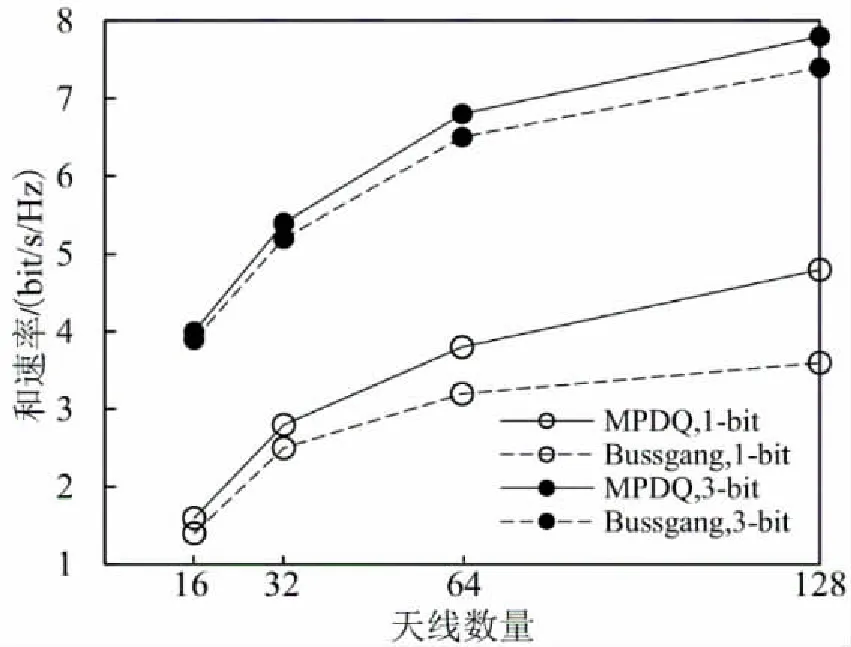
图5 两种模型在不同天线数量下的和速率

优化问题求解时的MPDQ算法的收敛性如图6所示。由基站天线数M=128，可知优化问题维度为128。从图6可以看出，本文提出的MPDQ算法具有较快的收敛速度，并且其迭代次数约为25次。为了更好地展现优化问题求解的优越性，对MPDQ优化模型与已有Bussgang模型的在量化精度分别为1-bit、3-bit及两种精度混合[19]时，使用优化问题求解的和速率(容量)进行对比，如图7所示。由图7可以看出，采用MPDQ优化后的和速率均明显高于Bussgang模型，并且两种精度混合架构下，MPDQ模型的优势更加明显。

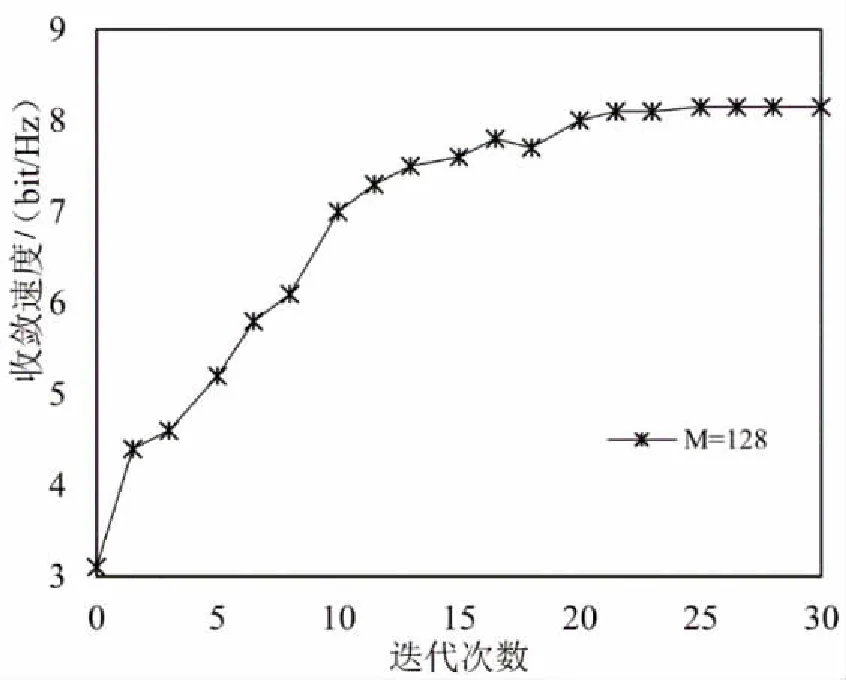
图6 优化问题求解MPDQ算法的收敛性

图7 不同量化精度下MPDQ优化模型与已有Bussgang模型对比

5 结束语

考虑在大规模MIMO系统中使用低精度量化器是一种降低成本的方法，但是传统的线性检测算法在低精度量化的情况下性能下降，误码率曲线出现“error floor”。本文研究了新的检测算法MPDQ在1-bit量化系统中的性能，并将其推广到n-bit量化系统，推导了MPDQ算法在n-bit量化系统中的迭代计算公式。通过仿真和分析，基于AMP的MPDQ算法在1-bit量化的情况下误码率性能依然很好，没有出现“error floor”，复杂度低。同时，3-bit量化误码性能与无限精度时相差很小，综合考虑性能和成本因素，3-bit量化应该是一种理想的方法。