高铁运行振动对大坝安全性影响特性研究

严 俊，魏迎奇，蔡 红，吴帅峰，乔芸芸，肖建章

(1.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京100048；2.北京水务咨询有限公司，北京100048)

1 研究背景

在高速铁路迅速发展的同时，其运营期间引起的地面振动问题也不容忽视。铁路振动不但影响沿线居民的正常生活与工作，还会影响沿线建筑物安全和精密仪器的制造和正常使用[1-5]，国际上也已将交通振动列为七大环境公害之一。例如，早在1995年，位于清华大学校园东侧的京山铁路，由于其产生的振动严重影响了校内精密仪器的正常工作，最后不得不将线路向东迁移800 m。与普通铁路相比，高速铁路多采用无砟轨道，列车运行速度快，开行频次高，如京津城际高速铁路每天开行列车约80余对，京沪高速铁路每天通过的列车100多次，其产生的环境振动问题更为突出。研究表明，高速铁路产生的地面振动与普通铁路相比虽然持续时间更短但是振动幅值更高[6]。

国内外对铁路引起的地面振动的研究主要包括地面振动振源模型和产生机理、振动的传播、振动对环境影响数值计算、振动波形的叠加4个方面：①在高铁振源模型及产生机理方面，国内外学者认为车辆系统和轨道系统的相互作用关系是高铁运行的主要振源，建立了经典的车辆-轨道稱合动力学模型，以研究列车振源荷载大小及特征；②在高铁引起环境振动传播规律方面，铁路地基土的物理力学性质(包括刚度、阻尼和分层厚度等)是铁路地面振动的主要影响因素之一，并发现当列车速度接近场地Rayleigh波的传播速度时，场地振动强度会突然大幅增加，且随距离增加高架桥段地面振动主频降低，振动的衰减曲线比较平滑，而路堤段地面振动主频随距离儿乎不变，振动衰减曲线存在多个反弹区能够；③在振动波形叠加方面，现有的波形叠加计算基本都集中在相同或相似的波形进行叠加，而针对不同性质的振动波形的叠加，如地震波和高速铁路列车运行引起的地面震动波相互叠加方面未有较好的处理方式；④在振动对环境影响的数值计算技术方面，大多采用车-建筑物-地基耦合系统的有限元分析模型，为研究高速铁路对环境的振动响应提供了很好的研究方法。

随着高铁的建设，由高速列车运行引发的环境振动问题越来越受到重视，但是目前国内外还鲜有高铁运行振动对大坝的安全性影响的研究。以京张铁路张家口灰场段为例，由于紧临京张高铁，随着高铁即将投入运行，高速列车带来的长期间歇性振动，是否会对灰坝的安全性造成影响，是否存在危及大坝安全的因素等，都是有待研究的内容。本文以京张铁路张家口灰场段为例，采用理论分析与数值模拟相结合的方法，对高铁运行振动影响下的大坝安全进行评价分析，在论证大坝安全性的同时，对存在影响安全的因素，提出适当的措施加以消除或降低危害使其在可控范围内。

表1 高铁运行实测振动统计值

1 高铁运行引起周围环境的振动特性和传播规律研究

高铁的快速运行容易造成铁路及周边地基的振动，而且随着振动向外传播，将引起周围环境的振动。高铁运行引起的振动既有水平向的振动，也有垂直向的振动，与地震波不同。此外，高铁引起的振动属于长时间周期性循环振动，地震波属于短时间内的突发一次性振动，两者之间存在较大的差异。为研究高铁运行对大坝安全的影响，开展了高铁线路结构各部位的振动情况和振动传播的衰减规律研究。

统计总结国内高速铁路运行时环境振动的实测值，如表1所示。从表1统计结果可以看出：①列车运行速度与周围环境的振动呈正比，速度越大，同等条件下环境振动越大，鉴于国内现阶段高速铁路运行平均最大速度为300 km/h(除复兴号外)，可选用此速度下的环境振动值；②随距离的增大，环境振动的峰值加速度减小；③振动在同一介质中传播，随着传播距离的增加缓慢向低频靠近，大多集中在30～70 Hz；④列车长度仅影响振动的持时而不影响振动加速度峰值，振动持时随车厢数的不同约为3～7 s。

将各条高铁实测振动加速度峰值绘制如图1所示，减小规律为指数型衰减，将所有测点振动加速度峰值采用指数函数进行拟合，并做测点的包络函数曲线，得到如图2所示。其中拟合曲线结果为amax=119.8e-0.156x，包络曲线公式为amax=110e-0.062x。

图1 测点加速度峰值衰减曲线

由包络曲线公式对100 m处振动加速度峰值进行预测计算，可得100 m处的加速度峰值为0.223 cm/s2。考虑安全性，计算时建议取值1 cm/s2，此时对应的加速度为0.001g。对开高铁运行时的加速度时程曲线见图3，迁安波单独作用时加速度时程曲线见图4，迁安波和高铁列车共同作用时加速度时程曲线见图5。

图2 测点加速度峰值衰减拟合线及包络线

图3 对开高铁运行时的加速度时程曲线

图4 迁安波单独作用时加速度时程曲线

图5 迁安波和高铁列车共同作用时加速度时程曲线

2 张家口灰场大坝工程概况

张家口发电厂位于河北省张家口市宣化区沙岭子镇，东距宣化约10 km，西距张家口约14 km，区内有北京-大同铁路、京张高速公路和207国道呈北西-南东向经过，南北向有地方公路相通，交通十分方便。张家口发电厂的贮灰场为山谷型灰场，东起陈家庄村西，西至太师湾东的部队仓库，由分别于1989年、1997年和2002年投入运行的东灰场、西灰场和靶场灰场3部分彼此相接组成。张家口电厂贮灰场位于电厂北侧山谷，距厂区约2 km。贮灰场范围东起陈家庄村西，西到太师湾东的部队仓库，由彼此相接的东灰场、西灰场和靶场灰场3部分组成，3座灰场均为分期修筑的山谷型灰场。

京张铁路张家口段距离东灰场坝脚最近地方约100.0 m，因此主要通过对东坝来开展振动分析。如图6所示，东灰场灰坝坝长1 070 m，初期坝最大坝高23 m；灰坝初期坝为均质土坝，坝长400 m，最大坝高17 m。3个贮灰场的初期坝断面类似，其坝顶宽6 m，上下游边坡为1∶2.5，排水棱体边坡为1∶1.5。

图6 东灰场典型断面示意

3 高铁运行振动对大坝安全性影响特性分析

3.1 计算条件

(1)有限元模型。根据工程基本情况，合理确定计算域大小，结合不同的材料分区，进行有限元网格剖分，以4节点四边形单元为主，局部辅以三角形单元进行过度。有限元网格见图7，其中节点数2 346个，单元数2 285个。

图7 有限元网格示意

(2)计算参数。取动剪应变为10-6时的动剪模量值为试验土料的最大动剪模量Gmax。初期坝堆石料、坝基角砾和粉煤灰的最大动剪模量Gmax与平均有效主应力σ0′的关系在双对数坐标上，Gmax与σ0′为直线关系，可用幂函数形式来表示，即

Gmax=KPa(σ0′/Pa)n

(1)

式中，σ0′为平均有效应力；pa为大气压力；K和n为试验参数，其值可由试验结果确定，整理结果见表2，具体计算过程中将对动剪模量比G/Gmax、阻尼比D数值化离散。

表2 最大动剪模量参数K、n值

(3)计算工况。根据京张高铁的运行情况，振动分析主要考虑以下情况：①分别考虑高铁一次运行振动(工况①)及运行2年循环振动(工况②)的影响，即考虑高铁每天运营时间6∶00～21∶30、每10分钟一趟，每日共计振动93次，每年振动33 945次；②遭遇7度地震时高铁运行安全分析(工况③)；③为论证大坝的安全性，还需要考虑高铁运行振动1次遭遇地震(工况④)和运行两年循环振动遭遇地震(工况⑤)时，对大坝的影响分析。

图8 坝体及坝基动位移等值线(单位：m)

3.2 仅高铁运行振动对大坝的安全性影响分析

工况①、②下高铁振动下大坝及坝基动位移分布如图8所示，可以看出：①坝体及坝基动位移等值线分布规律总体合理，其值基本上呈现从下至上逐渐增大的特点；②在高铁运行振动1次的作用下，整个大坝的水平向和竖向动位移极值微小(不超过0.02 cm)；在高铁运行振动2年的作用下，整个大坝的水平向和竖向动位移同样极值微小(也不超过0.02 cm)。

图9给出了高铁运行振动下坝体及坝基加速度等值线，可以看出：大坝加速度等值线总体分布合理，极值主要位于灰坝表面附近。仅高铁振动1次作用或累计振动2年时，大坝加速度反应很小。

图9 坝体及坝基加速度等值线(单位：m/s2)

此外，通过对高铁运行振动下大坝的动孔压和永久变形分析，仅高铁运行振动时灰坝不产生动孔压，不出现液化区域，且大坝基本不产生永久变形。

3.3 仅地震振动对大坝的安全性影响分析

在遭遇7度地震时，大坝及坝基动位移分布如图10所示。在地震作用下，整个大坝的水平向和竖向动位移极值分别为8.93、 5.66 cm。

图10 地震作用下坝体及坝基动位移等值线(单位：m)

图11为地震时坝体及坝基加速度等值线图，可见，极值主要位于灰坝表面附近，仅地震作用下水平向地震加速度放大倍数分别为2.72倍和2.78倍。

图11 地震作用下坝体及坝基加速度等值线(单位：m/s2)

通过计算分析，仅地震作用时，灰坝坝体基本不产生动孔压，不会出现液化区域；灰坝的永久变形随着振动时间有所积累，即当土体单元的加速度超过屈服加速度时，产生残余变形增量，并不断累积，至振动结束时达到最大值。仅地震作用时，灰坝的永久变形为6.406 cm。

3.4 高铁运行振动遭遇地震时对大坝的安全性分析

大坝在考虑高铁振动影响下遭遇7度地震时大坝及坝基动位移等值线如图12所示，可以看出，在高铁运行振动作用下，整个大坝的水平向和竖向动位移极值微小(不超过0.02 m)；在地震作用下，整个大坝的水平向和竖向动位移极值分别为8.93 cm和 5.66 cm；在高铁运行振动联合地震作用时，整个大坝的水平向和竖向动位移极值分别为8.93 cm和5.66 cm；在高铁运行振动联合地震作用2年后，整个大坝的水平向和竖向动位移极值分别为8.93 cm和5.66 cm，基本未发生增长。

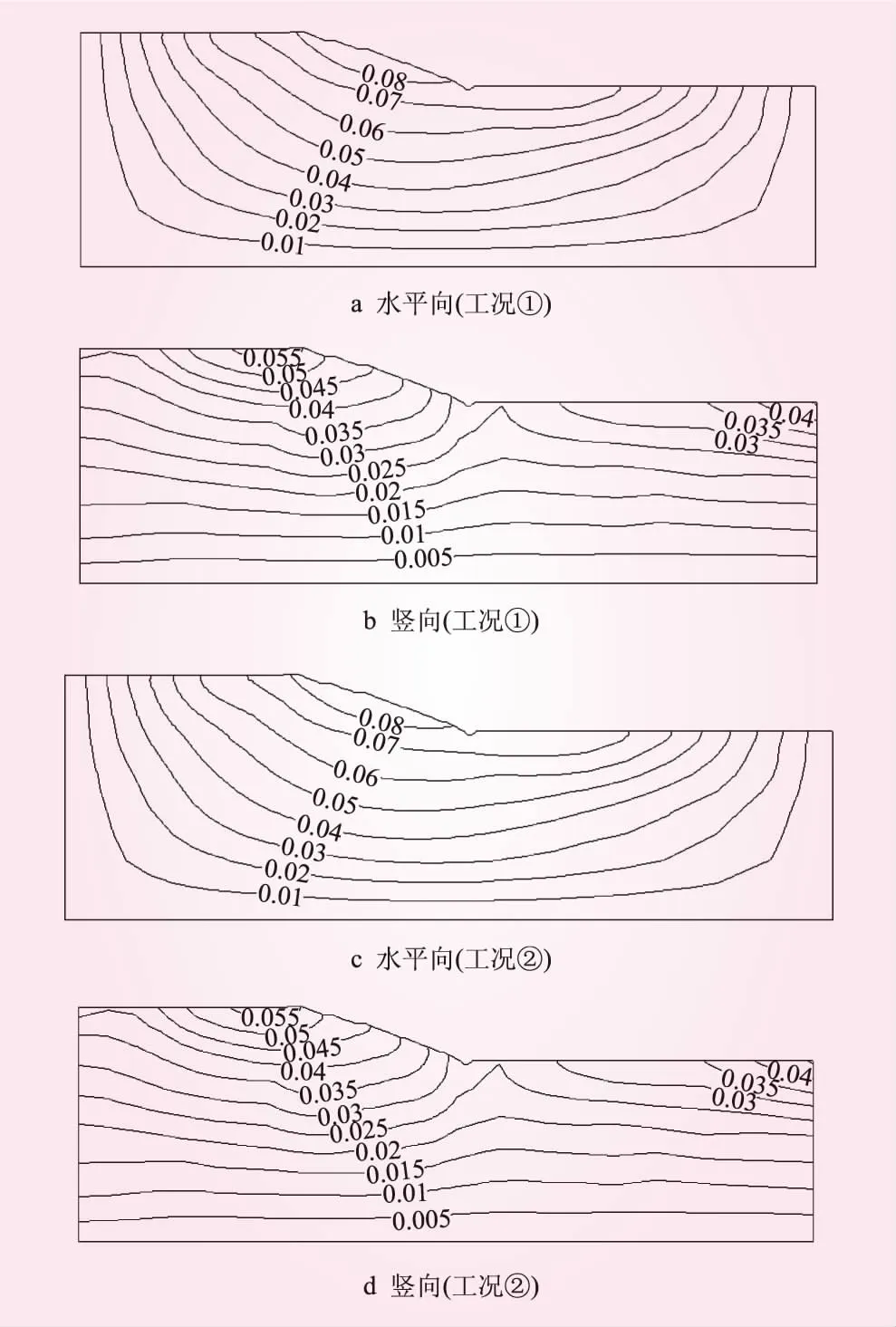
图12 地震+高铁振动下坝体及坝基动位移等值线(单位：m)

工况①、②下坝体及坝基加速度等值线如图13所示，可见，考虑高铁振动影响下遭遇7度地震时，加速度极值主要位于灰坝表面附近。仅高铁振动作用时，大坝加速度反应很小；仅地震作用和地震+高铁振动1次时水平向地震加速度放大倍数分别为2.72倍和2.78倍，竖向加速度放大倍数分别为4.53倍和4.54倍；考虑地震+高铁振动2年后水平向地震加速度放大倍数2.78倍，竖向加速度放大倍数为4.54倍。

图13 地震+高铁振动下坝体及坝基加速度等值线(单位：m/s2)

通过计算分析，在地震联合高铁振动作用1次及2年后，灰坝坝体仍未产生较大的动孔压，在灰坝浅表层未出现液化区域。此外，仅高铁运行振动时灰坝不产生永久变形。地震作用及地震联合高铁振动时，灰坝的永久变形随着振动时间有所积累，即当土体单元的加速度超过屈服加速度时，产生残余变形增量，并不断累积，至振动结束时达到最大值。仅地震作用时，灰坝的永久变形为6.406 cm，地震联合高铁振动作用时，灰坝的永久变形为6.415 cm，地震联合高铁振动作用后2年，灰坝的永久变形为6.420 cm，高铁对灰坝的永久变形影响微小。

5 结 论

本文采用理论分析与数值模拟相结合的方法，在系统总结高铁运行振动对周边环境的影响规律基础上，对高铁运行振动影响下的张家口灰场大坝安全进行评价分析，结果表明，在一定距离下，高铁运行振动对大坝的安全性影响较小：

(1)大坝动位移从坝基至坝顶逐渐增大，在高铁运行振动作用下(1次及2年)，整个大坝的水平向和竖向动位移极值不超过0.02 m；在地震作用下，水平向和竖向动位移极值分别为8.93 cm和 5.66 cm；在高铁运行振动联合地震作用(1次及2年后)时，水平向和竖向动位移极值分别为8.93 cm和5.66 cm，高铁运行振动对坝体动位移的影响很小。

(2)仅高铁运行振动(1次及2年)时，大坝加速度反应很小，极值约0.003g；仅地震作用和地震+高铁振动(1次及2年后)水平向地震加速度极值分别为0.409g和0.418g，竖向加速度极值分别为0.453g和0.454g，高铁对大坝加速度影响很小。

(3)仅高铁运行振动(1次及2年)时，灰坝不产生动孔压，无液化区域；仅地震作用时灰坝坝体未出现较大的动孔压，不会在灰坝浅表层出现液化区域；地震联合高铁振动作用(1次及2年后)下，灰坝坝体也不会出现较大的动孔压，灰坝浅表层不存在液化区域，高铁对灰坝动孔压和液化区域影响很小。

(4)仅高铁运行振动(1次及2年)时，灰坝不产生地震永久变形，仅地震作用时灰坝的永久变形为6.406 cm，地震联合高铁振动作用1次时灰坝的永久变形为6.415 cm，运行2年后永久变形为6.420 cm。高铁对灰坝的永久变形影响微小。