电子束氨法脱硫反应器内部剂量率的模拟计算

王棋赟 李建军 李升华

(1.四川大学建筑与环境学院, 成都, 610065;2.国家电投集团远达环保工程有限公司, 重庆, 4011222)

电子束氨法脱硫(EA-FGD)是一种等离子体烟气处理技术，基本原理是利用高能电子束轰击锅炉烟气生成的OH、O3等强氧化性产物将烟气中的SO2和NOn氧化，继而与H2O和NH3反应生成(NH4)2SO4或NH4NO3的过程。电子束氨法脱硫的主工艺系统是烟气辐照处理系统，它由电子加速器和反应器组成。系统运行时，反应器内电子束呈一个几何轮廓为扁平状四棱锥帘状射束。

鉴于源的不规整特性，加之EGS4在处理粒子输运问题上更为灵活、涉及物理过程也更全面[1]，过去在EA-FGD反应器设计时通常采用EGS4程序进行模拟计算。然而EGS4程序运行前，需要用户用高级计算机编程语言构建粒子输运的空间环境等诸多信息，这对设计人员编程能力提出了较高的要求。MCNP与EGS4同属于蒙特卡罗方法的分支，比之EGS4，MCNP通过定义曲面来构建空间体，且不需要像EGS4那样描述粒子穿透不同区域的形式，也不需要用户自行编写代码生成伪随机数；在解决了MCNP对不规整源的描述困难后，如能验证MCNP程序计算结果误差在可接受范围内，则可以在今后类似设计中，一定程度上降低设计的难度。

本文利用“小孔成像”原理来解决MCNP对不规整源的描述困难。通过模拟文献[2]的试验场景，将结果与试验值进行比较，验证MCNP用于电子束氨法脱硫反应器内部剂量率计算的可行性。

1 模型建立

试验电子束氨法脱硫烟气辐照处理系统，装置采用碳钢反应器[2]，反应器尺寸为〔140 cm(内径)×200 cm(长)〕，钛窗尺寸为(100 cm×50 cm×0.003 cm)，两层钛窗之间间距为7 cm，电子束流偏转点到下层钛窗上表面距离为130 cm(如图1)。此外，电子束能量为0.57 MeV，束流强度是5 mA，辐照时间为30 s。

利用“小孔成像”原理模拟电子束氨法脱硫装置加速器引出窗[3]出射的电子束，即在MCNP源栅元描述时将此抽象成一个位于“圆筒”内部的粒子源，而在圆筒的底面存在一个“矩形孔”，长宽比例与钛窗相同，如图2所示。

通过将除“矩形孔”外的圆筒栅元的重要性设置为零，即可对这些点源发射的“多余”粒子不进行跟踪，但利用“小孔成像”建立的源会因这些“多余”的粒子引入一个几何修正因子η，将实际粒子数进行一定程度的“放大”，以抵消那些多余的粒子。该值可以通过把矩形孔设置成探测栅元，记录矩形孔中的粒子通量反算得出。关于轫致辐射，因为在入射电子能量为几个兆电子伏时，其能量损失方式是以电离能量损失为主。两者之比为[4]：

(1)

图1 反应器束流廓面示意图

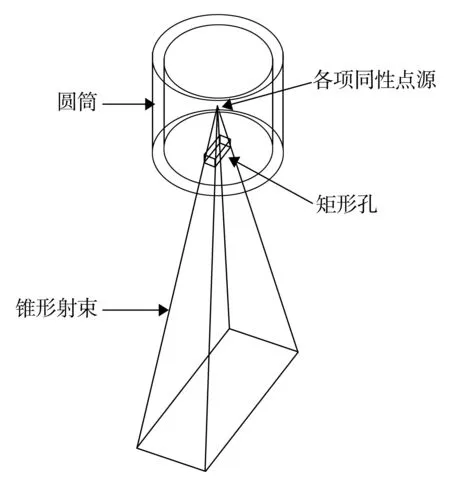
图2 棱锥射束引出示意图

式中，(-dE/dx)r为单位路程辐射能量损失；(-dE/dx)e为电离能量损失；Z为介质原子序数；E为电子束能量，MeV。

文献[2]的试验是在空气介质中进行的，以氧原子的序数计算，可知当入射电子能量为0.57 MeV时，轫致辐射与电离辐射能量损失之比为0.57%。因此，在计算反应器内部剂量场时，可以忽略轫致辐射的影响。

2 计算过程与结果

试验采用的木架模型，通过两次更换木架的方向分别测量3个方向的剂量场，即反应器剖面剂量场、反应器随电子入射深度方向的剂量场和反应器中心截面的剂量场[2]，试验方案示意图3。

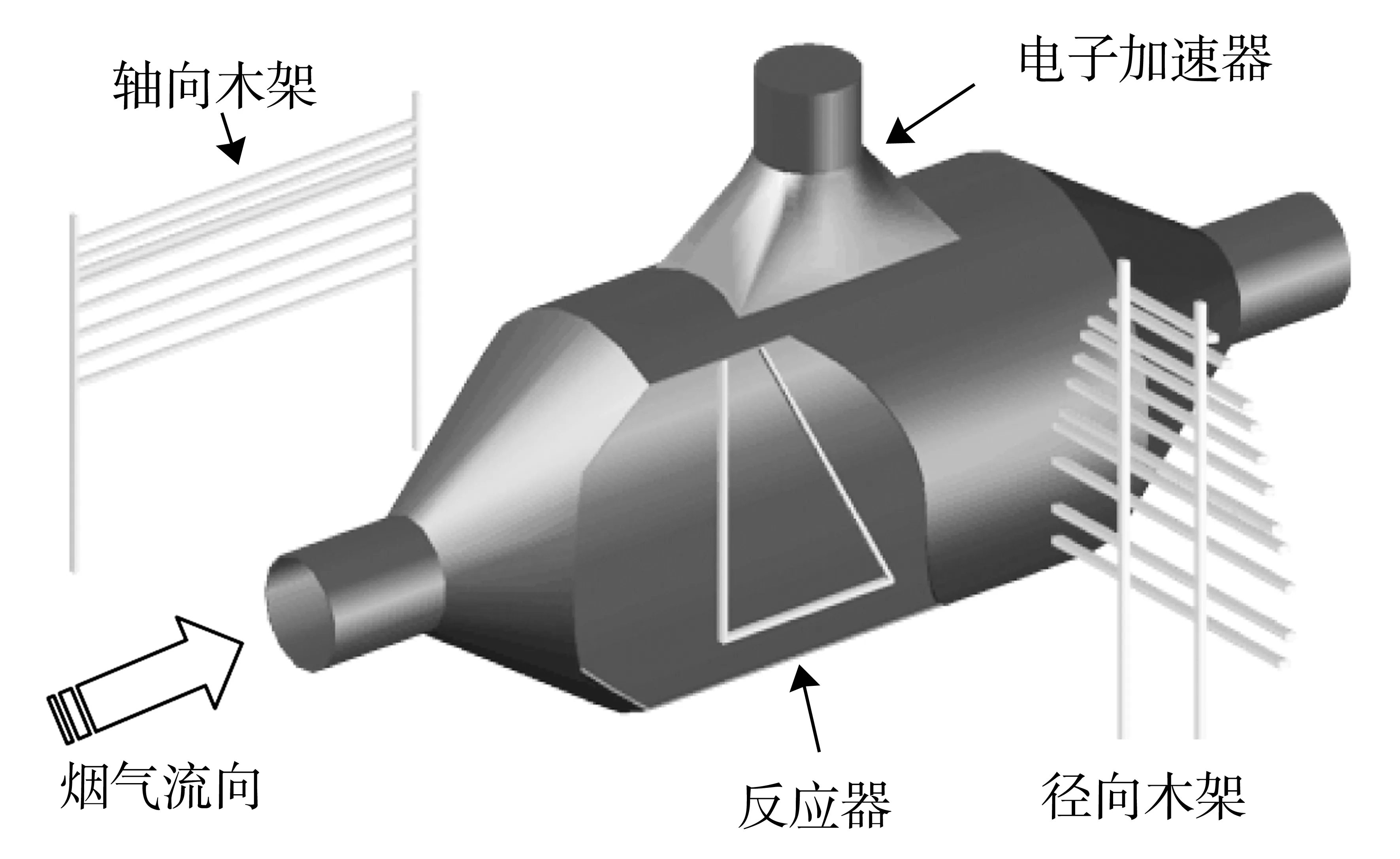
图3 试验方案示意图

文献[2]中未介绍木架的尺寸大小及木料密度，考虑过于细长的方木可能因为自重而弯曲变形，故验证过程暂按方木尺寸2 cm×1 cm考虑，密度按0.4 g/cm3计。计算时，MCNP抽样粒子数为1×108，用F4卡计数，计数栅元体积为8 cm3，结果标准差均满足统计检验(σ<0.1)。

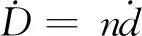
(2)

其中，

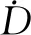
以剖面试验中木架上第一排中点处剂量率计算为例，其剂量率与30 s累积剂量计算结果为：

式中，D为累积时间内的吸收剂量，kGy；t为积累时间，s。

MCNP计算中所使用的剂量乘子卡点值函数DE-DF系数(即通量-剂量转化系数f)可通过《辐射剂量学》[5]中给出的电子质量碰撞本领计算求得，如能量为0.6 MeV的单能电子对应的质量碰撞本领s/ρ=1.743 MeV·cm2/g，则可计算得出转换系数：

综上，可得到反应器剖面剂量场(示于图4)，图5给出了实测的反应器剖面剂量场。

由图4知，因木架(截面尺寸2 cm×1 cm)的屏蔽散射作用而导致的对剂量场的影响效应：木架使反应器内剂量场出现一个“陡降区”，在木架下方，剂量场有所回升，形成一个类似“山坳”的剂量场区间，而这一现象是图5实测剂量场所没有的，图5左上区域等剂量线内凹，可能就是木架左端采用木料根部，密度比右侧更高的原因所导致的。为此，将木架截面尺寸修改为1 cm×0.5 cm重复计算，然则，这种“山坳效应”仍然存在。

文献[6,7]用EGS4对该实验进行了模拟，模拟过程忽略了木架的影响，设置抽样粒子数为1×106，可得到满足统计学检验的计算结果(σ<1%)。为与之对比，在MCNP建模过程中删除木架栅元，忽略木架的影响，将计算结果分别与文献[2,6,7]的结果进行比较(表1)。

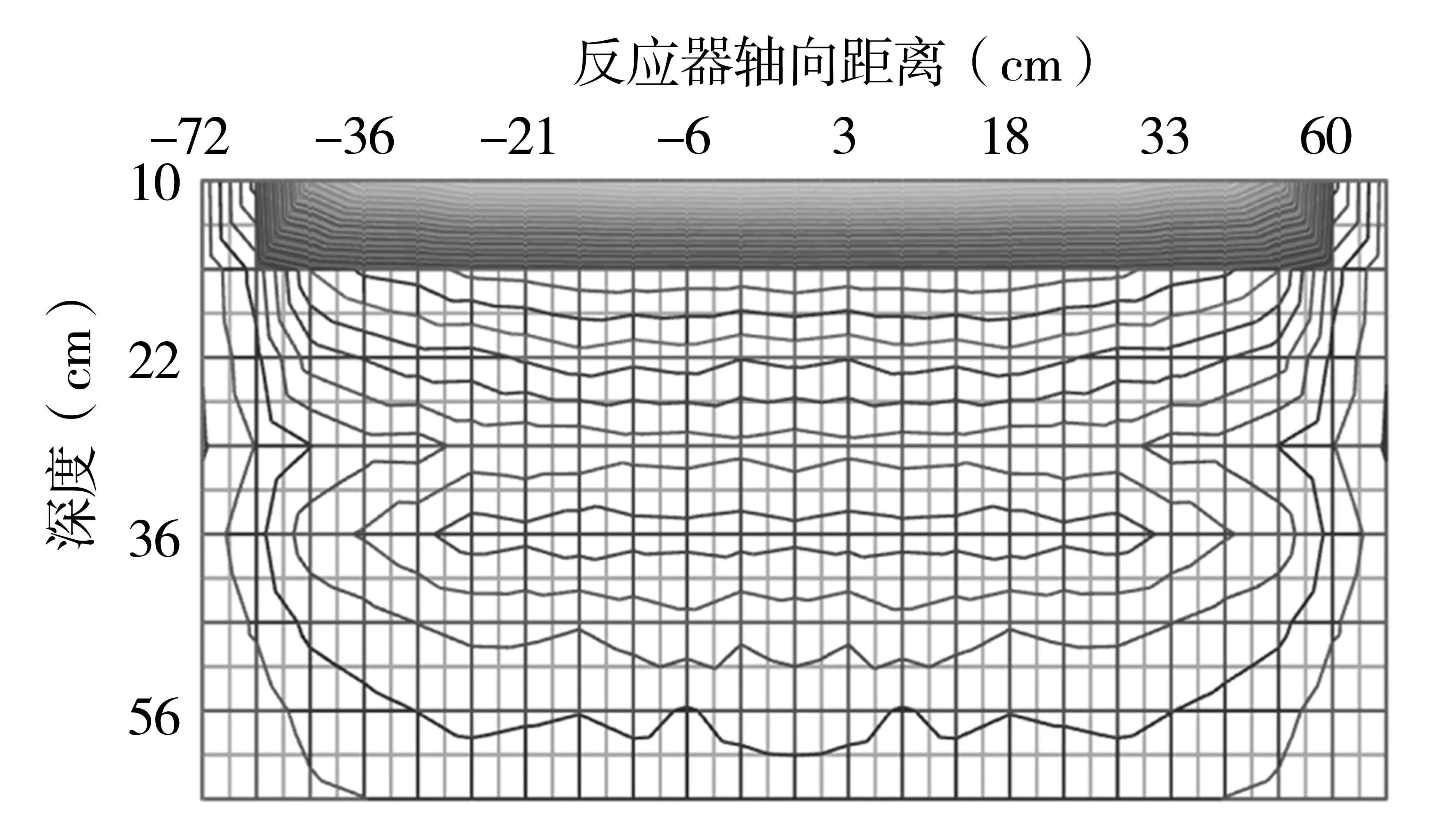
图4 MCNP计算所得反应器剖面剂量场

图5 反应器剖面剂量场(实测)[1]

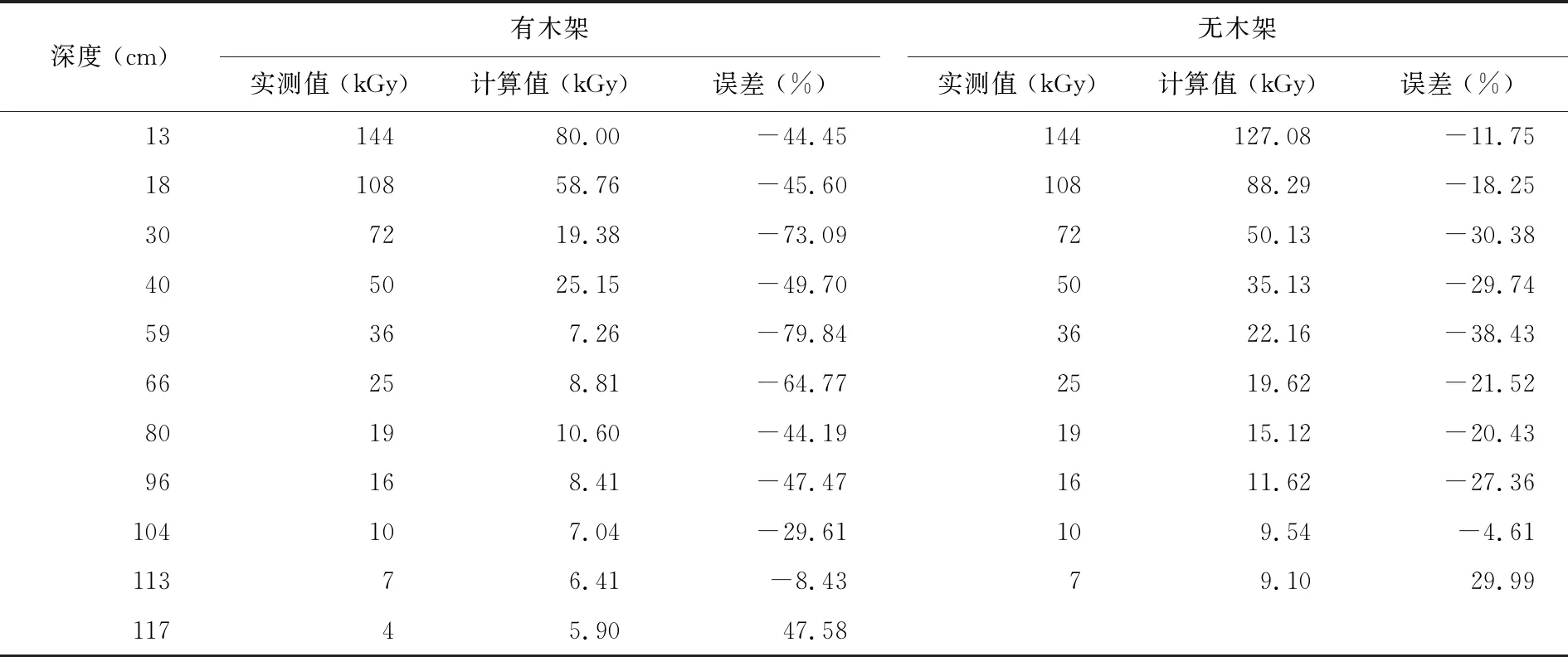
表1 MCNP模拟结果与试验值的对比

由表1可见，MCNP计算值与试验拟合值间最小绝对值偏差为8.43%；最大绝对值偏差为79.84%，出现在反应器木架深度区域；完全去掉木架后得到的计算值(理论值)，其与试验值的最大绝对值偏差也达到38.43%，这与文献[6,7]EGS4程序的结果偏差34.7%较为接近。

表2给出了相同几何条件下，MCNP与EGS4模拟计算结果，两者最大绝对值偏差为25.7%，可能是EGS4本身考虑的物理过程更全面、且具体计算时EGS4选取的探测栅元体积更大所致。

程序验算结果与文献[2]实验结果的较大误差(实验结果未见理论分析中出现的“山坳效应”)可能是实验中木架位置与理论计算有一定偏离，且实验值经Matlab拟合修正后引入的。

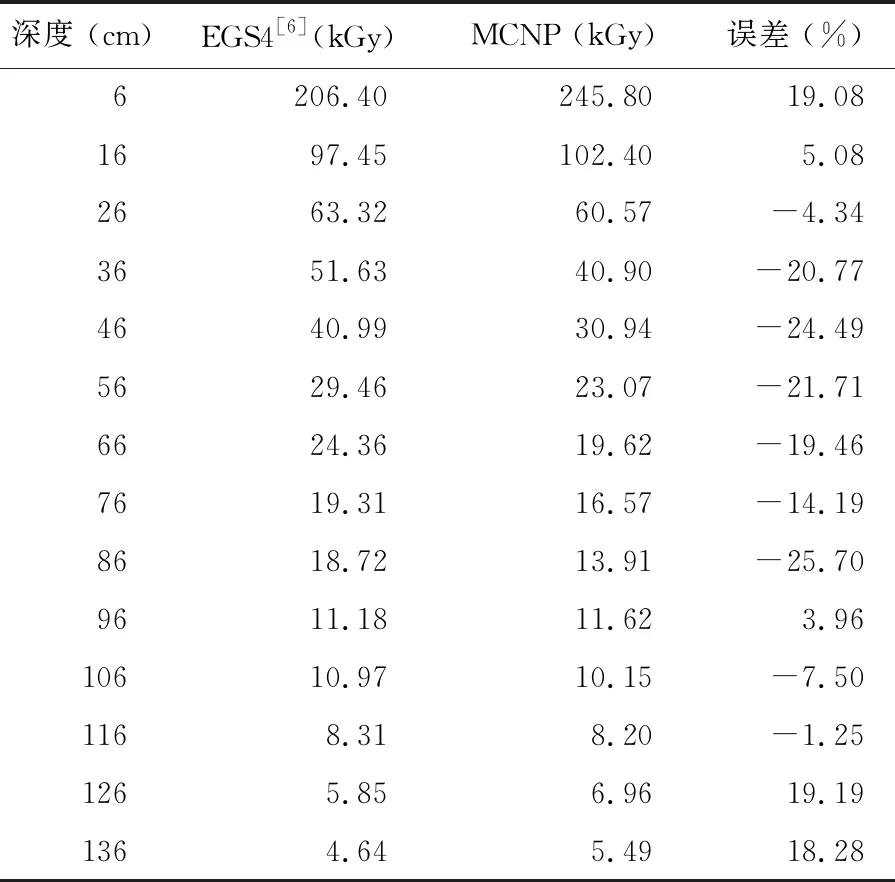
表2 MCNP模拟结果与EGS4模拟结果对比(无木架)

3 结语

MCNP与EGS4各有侧重。相比MCNP，EGS4涉及的物理过程更全面，在电子模拟过程中，EGS4比MCNP更为适用，这也是前人通常采用EGS4程序模拟电子束氨法脱硫反应器内部剂量率的原因，但EGS4采用高级计算机编程语言进行建模输入，不如MCNP简单，从这个角度来说，MCNP可操作性要好于EGS4。结果表明：

(1) 用MCNP“小孔成像”的方法模拟电子束氨法脱硫反应器内部剂量场总体是可行的。

(2) 为减小测量误差，试验可改用更细的轻金属丝线绑扎固定剂量片的方法，以消除固定装置对反应器内部剂量场的影响。