旋转圆盘内不同转速的空化特性研究

葛新峰，徐 旭，来亦姝，沈明辉，江启峰，陈慧楠，宁望望

（1．河海大学 能源与电气学院，江苏 南京210098；2．河南大学，河南 开封475000；3．国网河南省电力公司新乡供电公司，河南新乡453004；4．流体及动力机械教育部重点实验室（西华大学），四川成都610039）

随着水力机械在各个行业的广泛应用，空化性能已经成为水力机械在设计、加工及运行中必须予以考虑的关键因素之一。研究发现空化是造成水力机械表面变形、材料脱落，甚至穿孔的主要原因，会导致水力机械发生振动、效率下降，严重时可能引发重大的生产安全事故，造成严重的经济、人员损失。因此，如何减小空蚀危害，提高水力机械的抗空化性能已经成为国内外水力机械领域的重要研究方向之一［1］。

很多学者利用试验和CFD数值模拟对水力机械的抗空化性能进行了研究。ZHANG Yuning等［1］利用激光产出空泡对空化的记录进行了研究。JI B等［2-3］对水轮机叶片的翼型开展了研究。LI Deyou等［4］对水轮机尾水管内的空化展开了研究。曹树良等［5-6］对离心泵转轮内空化流动情况进行了分析。施卫东等［7］运用数值模拟技术分析轴流泵不同叶顶间隙对去空化性能的影响，结果表明叶顶间隙越大，泵的临界空化数越大。李晓俊等［8］对带诱导轮离心泵的空化流动情况进行模拟，得到了离心泵空化条件下流道的空泡分布规律和扬程下降的规律。

目前研究空化空蚀现象的技术很多，但常用的主要包括文丘里管型、振动型、旋转圆盘型三种试验装置，对旋转圆盘的试验研究主要围绕着对材料的空化空蚀研究展开，但是还没有关于旋转圆盘内部流态特性的研究，因此有必要对旋转圆盘内的流动特性进行研究。笔者模拟不同转速对旋转圆盘空化性能的影响，得到了旋转圆盘的转速n与空化数 σ的关系曲线。

1 计算模型及计算方法

1．1 模型建立和网格划分

旋转圆盘试验装置见图1。旋转圆盘试验系统可用于研究材料的空化和空化损伤，该系统包括储水池、泵、进水管、转盘装置、出水管和电动机6个主要部件。试验过程中，由水泵通过进水管从水池中抽水，经过旋转圆盘，通过回水管返回水池。当水循环时，电动机驱动旋转圆盘，最高转速可达3 000 r／min。 图1（b）试验圆盘上大孔为试件安装孔，小孔为空蚀源，试验过程中从小孔产生空化气泡，沿着水流方向在圆形试件上溃灭，对试件造成侵蚀。

图1 旋转圆盘试验装置和试件

1．2 湍流模型与空化模型

1．2．1 湍流模型

本研究使用CFD数值模拟软件，采用的湍流模型为SST k-ω湍流模型［9-10］。该模型在近壁面处即边界层内层采用k-ω湍流模型，但在自由剪切层内和边界层边缘使用标准k-ω湍流模型，表达式分别为

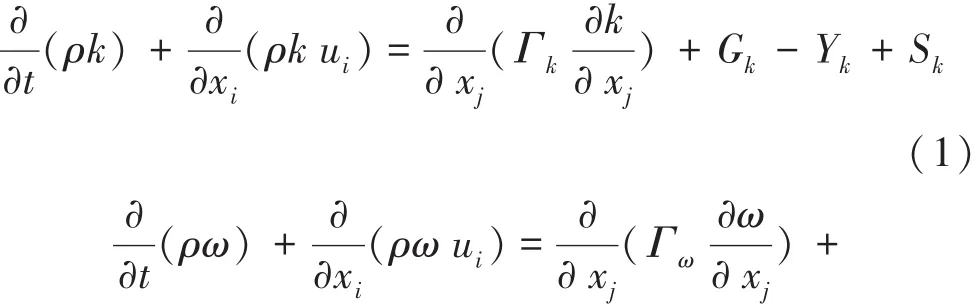
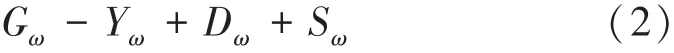
式中：k为紊功能；ω为耗散率；ui为时均速度；Gk为平均速度梯度引起的湍流动能；Gω为ω方程；Γk、Γω分别为k与ω的有效扩散项；Yk、Yω分别为k与ω的发散项；Dω为正交发散项；Sk与Sω为用户自定义项。

SST k-ω湍流模型具有求解方程数少、计算速度快、精度高等优点，为广泛的湍流模型［11］，比较符合旋转圆盘空化试验装置的实际工况。

1．2．2 空化模型

Zwart-Gerber-Belamri模型为CFX软件的默认空化模型，它是基于简单的Raylrigh-Plesset方程提出的，本研究采用该模型。该模型认为同一流场中所有气泡尺寸都相同，其空化模型方程如下：

当 P0≤PV时

当 PV＜P0时

式中：Re、Rc分别为蒸发速率及凝结速率；fvap、fcond为蒸发和凝结时的经验系数，分别取50、0．01；anuc为气核初始体积分数；av为气核体积分数；RB为气泡半径；ρv、ρl分别为气泡密度、流体密度；P0为基准静压力，本文采用旋转圆盘进口压力Pa；PV为液体的饱和汽化压力，取水在25℃下的饱和汽化压力。

1．3 边界条件

采用ANSYS CFX 15．0进行数值模拟计算，进口边界条件为总压力进口，进口压力P0＝0．1 MPa；出口边界条件采用质量流出口，出口流量 V＝2．04 m3／h；系统的参考压力设为0 Pa，水在25℃时的饱和汽化压力为3 574 Pa；壁面边界设置为无滑移边界，即壁面处流体速度为0，同时使用Automatic wall treatment壁面函数处理湍流面。在该边界条件下，通过改变旋转圆盘的转速来研究其对旋转圆盘空化性能的影响。

2 结果分析

2．1 旋转圆盘空化数

空化是液体内局部压力降低时液体内部或液固交界面上蒸气或气体空穴（空泡）形成、发展和溃灭的过程［12］，为了更加准确地描述旋转圆盘的空化性能，在数值模拟计算时引入一个无量纲数σ用来描述其空化发生的可能性，其表达式为式中：u0为基准速度，本文采用水流进入旋转圆盘中空蚀源时的水流圆周速度，m／s。

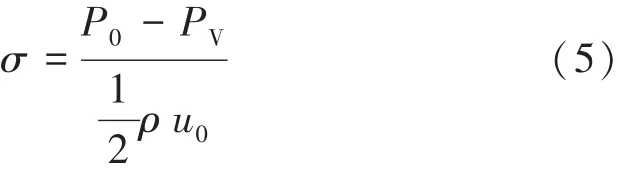
图2（a）为水流进入空蚀源时的流速图，水流冲击旋转圆盘时在高速旋转圆盘的带动下做加速离心运动，而水流进入旋转圆盘中空蚀源时水流速度就是u0（即图2（a）中的1点），该点也为图中速度最大的点。图2（b）为水流流出空蚀源的流速图，水流流出空蚀源后做加速离心运动流出旋转圆盘。

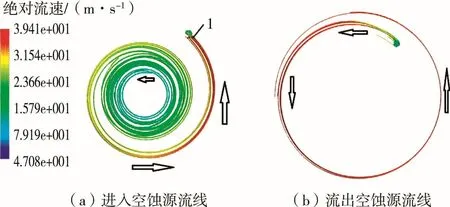
图2 水流流进和流出旋转圆盘空蚀源的流线

在进口压力为0．1 MPa时改变转速，得到转速n与空化数σ的关系，见表1，进而得到旋转圆盘转速n与空化数σ的曲线，如图3所示。

表1 转速n与空化数σ的关系

由图3可知，旋转圆盘转速n与空化数σ成幂函数关系，随着转速的上升，空化数σ不断降低，而空化数越小，空化越严重，因此随转速上升空化变得更严重。

图3 转速n与空化数σ关系曲线

2．2 转速对旋转圆盘空蚀源附近压力的影响

在进口压力为0．1 MPa时对6种不同转速工况下旋转圆盘进行数值模拟，得到其在不同转速下空蚀源附近的压力分布情况，如图4所示。

当转速为 1 500 r／min、σ＝0．415 时，其空蚀源右边产生低压，上下产生高压，低压为63．4 kPa，大于水的饱和汽化压力，所以不会产生空化；随着转速的上升，产生的最低压力不断降低；当转速为2 000 r／min、σ＝0．232时，最低压力开始低于水的饱和汽化压力，开始产生空化；转速进一步提高，空蚀源左边低压区压力进一步降低、面积进一步扩大，空蚀源上下的高压区出现压力升高、面积扩大的情况，这些都最终导致空化现象越来越严重。

通过对不同转速下绝对压力分布云图的分析，得出以下结论：随着转速的上升，在旋转圆盘空蚀源的右侧产生低压，上下产生高压，转速越高其产生的低压就越低，高压就越高，低压区和高压区的面积就越大，低压区越靠近空蚀源压力越低，空化就越严重。

图4 空蚀源附近绝对压力分布云图

2．3 转速对旋转圆盘空化性能的影响

本节主要研究不同转速n对旋转圆盘空化性能的影响。对进口压力为0．1 MPa、6种不同转速工况下旋转圆盘空化性能进行分析，得到不同转速下空蚀源附近的气泡体积分数情况，如图5所示。

空化的过程可以分为无空化、初生空化、空化发展及完全空化4个阶段。由图5不同转速下空泡体积分数分布云图可以看到：当转速为 1 500 r／min、σ＝0．415时，旋转圆盘上没有出现空泡，所以此时旋转圆盘上并没有产生空化；随着转速的上升，当转速为2 000 r／min、σ＝0．232 时，旋转圆盘空蚀源外边缘开始产生空化，此时为初生空化；随着转速的进一步上升，可以非常清楚地看到旋转圆盘上出现空泡的面积在不断扩大，其所出现的空泡体积分数也越来越大；当转速为3 000 r／min、σ＝0．102 时，空化现象已经非常严重，旋转圆盘空蚀源处产生的空泡面积已经很大，而且越靠近空蚀源边缘颜色就越深，其所产生的空泡体积分数越大空蚀就越严重；在所研究的转速范围内，随着转速的上升，旋转圆盘上的空化从无到有，空化一直在发展，变得越来越严重。

图5 空蚀源附近空泡体积分数分布云图

2．4 试验验证

本节主要利用现有的旋转圆盘试验装置对数值模拟结果进行验证。对进口压力为0．1 MPa、出口流量为2．04 m3／s、转速为 2 500 r／min 的旋转圆盘空化空蚀过程进行分析，与数值模拟结果进行比较，如图6所示。

图6 转速为2 500 r／min时试件在旋转圆盘装置中的空化情况与数值模拟结果

空化是一个过程，而空蚀是因空化的产生而在试件表面造成破坏的结果，数值模拟只能反映该工况下其所产生的空泡分布的大小。如图6（b）所示，通过数值模拟结果可以清楚地看到在旋转圆盘空蚀源的右侧空泡体积分数很大。同时在图6（a）中也可以清楚地看到在旋转圆盘空蚀源的右侧（试件表面）产生了大量空泡，进而验证了数值模拟的准确性。

3 结 论

本文研究了不同转速下旋转圆盘的空化性能，建立了圆盘试验装置全流道几何模型，使用CFD数值模拟软件模拟不同转速工况下的情况，对其结果进行分析，得出以下结论。

（1）通过分析旋转圆盘转速n与空化数σ关系曲线可知，旋转圆盘转速n与空化数σ成幂函数关系，随着转速的上升，空化数σ不断降低，而空化数越小，空化越严重。

（2）随着转速的上升，在旋转圆盘空蚀源的左侧产生低压，上下产生高压，转速越高其产生的低压就越低，高压就越高，低压区和高压区的面积就越大，低压区越靠近空蚀源压力越低，空化就越严重。

（3）当转速为 2 000 r／min、σ＝0．232 时，旋转圆盘空蚀源外边缘处开始产生空化；随着转速的上升，旋转圆盘上出现空泡的面积不断扩大，而且越靠近空蚀源边缘所产生的空泡体积分数越大，空蚀就越严重；在所研究的转速范围内，旋转圆盘上的空化从无到有，空化一直在发展，变得越来越严重。