增生算子扰动方程的迭代解
2019-08-23张芯语张树义
张芯语, 张树义
(渤海大学 数理学院, 辽宁 锦州 121013)
文献[1]在一致光滑Banach空间中,讨论了形为
f∈Tx+Sx,x∈D(T)
的扰动方程解的逼近问题, 其中T:D(T)⊂X→2X是多值m-增生算子,S是α-强增生算子.文献[2]将上述成果扩展到了一般的实Banach空间中, 讨论形为
f∈Tx+Ax+Cx,x∈D(T)
的扰动方程的Ishikawa和Mann迭代的收敛问题,其中T同上,A是一致连续增生算子或强增生算子,C是单值算子.文献[3-5]研究了广义Lipschitz非线性算子不动点迭代逼近问题.文献[6]利用锥压缩不动点定理, 得到了非线性Dirichlet型三点边值问题正解存在性的条件.近年来,文献[7-19]研究了包括增生算子在内的几类非线性算子迭代收敛问题.受上述工作的启发,本文在集值广义Lipschitz条件下研究这类扰动方程解的具误差的迭代序列的收敛性, 由于集值广义Lipschitz一定是值域有界的, 而反之未必成立.因此,本文的结果从以下4方面推广和改进了文献[2]中的相应结果:
1)T(D),(I-A)(D),C(D)有界性条件被广义Lipschitz条件所代替;

3) 将迭代程序推广到具误差的迭代程序;
1 预备知识
设X为实Banach空间,映射T:D(T)⊂X→2X称为增生的,如果对任意的x,y∈D(T)和r>0,有
它可等价定义为:对任意的x,y∈D(T),存在j∈J(x-y),使得 〈u-v,j〉≥0,∀u∈Tx,v∈Ty.映射T:D(T)⊂X→2X称为m-增生的,如果T是增生的,且对任意的λ>0,R(λI+T)=X.映射T:D(T)⊂X→2X称为k-强增生的,如果存在k>0,使得对任意的x,y∈D(T),存在j∈J(x-y),有
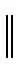
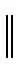
定义1[3]T:D→D称为广义Lipschitz的,如果存在L≥1,∀x,y∈D,有
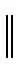
注意到若T是Lipschitz的,以及值域{Tx},x∈D有界,则T是广义Lipschitz的,但反之一般不成立,反例见文献[4].
定义2[5]T:D→2E称为集值广义Lipschitz的,如果存在L≥1,∀x,y∈D,有
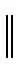
其中,u∈Tx,v∈Ty.
引理1[4]设{an}n≥0,{bn}n≥0,{cn}n≥0和{en}n≥0是4个非负实数列,满足条件,存在正整数n0,当n≥n0时,有
an+1≤(1-tn)an+bnan+cn+en,

2 主要结果
定理1 设T:D⊆X→2X是集值广义Lipschitzm-增生算子,A:X→X是单值广义Lipschitz增生算子,C:X→X是单值广义Lipschitz非线性算子,假定存在k,r>0,k>r,使得C-kI是具有常数r>0的Lipschitz连续算子,{αn}n≥0,{βn}n≥0,{γn}n≥0,{δn}n≥0是[0,1]中的4个实数列,{un}n≥0,{vn}n≥0是D中的有界序列,满足下列条件:
1)αn+γn≤1,δn+βn≤1;
2)αn→0,βn→0,δn→0(n→∞);
对f∈X,x0∈D,由下式定义的具有误差的Ishikawa迭代序列

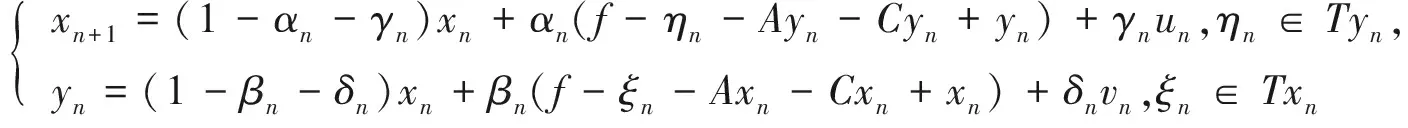
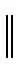
证明 因为{un}n≥0,{vn}n≥0为D中的有界序列,所以
记T0q∈Tq,使f=T0q+Aq+Cq.由式(1)有

由T+A的增生性, 据式(2)有
对式(3)右端第4项、第5项和第6项做如下估计.式(3)右端第4项,由式(1)有
式(3)右端第5项,由式(1)有
式(3)右端第6项,由式(1)有
把式(4)~式(6)代入式(3)有
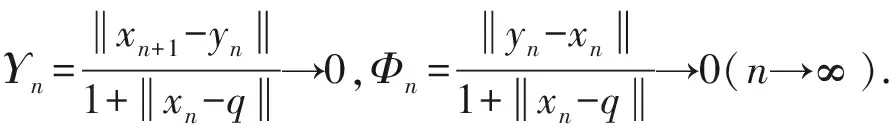
因αn→0,βn→0,δn→0,Υn→0,Φn→0(n→∞),所以存在正整数n0,使得n≥n0,有
从而n≥n0,由式(7)有

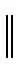
an→0(n→∞), 即xn→q(n→∞).
证毕.
在定理1中取δn=βn=0,可得定理2.
定理2 设T、A、C、k、r如定理1所述.对f∈X,x0∈X,由Mann迭代序列
得到的{xn}⊂D.{αn}n≥0,{γn}n≥0是[0,1]中的实数列,{un}n≥0是D中的有界序列且满足下列条件:
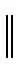
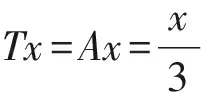
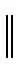
从而
据此有
于是满足定理1中的所有条件. 但因T,C和I-A的值域均无界,因此文献[2]中的定理1对此例失效.
