凯夫拉纤维增强型挠性接管管体变形检测方法及数值分析

范宇琦 ，孙谦 ，吕志强 ，卜文俊*

1海军工程大学船舶振动噪声重点实验室，湖北武汉430033

2海军装备部，北京100071

3海军工程大学振动与噪声研究所，湖北武汉430033

0 引 言

为了降低船舶振动噪声的传递，提高管路系统的抗冲击能力，在船舶管路系统中大量应用了凯夫拉纤维增强型挠性接管（Filament-Wound Flexible Pipe，FW-FP）［1-2］。在挠性接管的使用过程中，管体会发生3种类型的变形：第1类是在充压状态下的变形；第2类是在外力（如剪切力、轴向力）作用下的变形，且均属于管体工作状态下的正常变形；第3类是局部异常变形，它是由于管体内部流体介质的压力变化而导致管体内部发生疲劳变形，一般发生在管体应力敏感薄弱的局部区域，当异常变形超过一定的范围后，会加速管体的破裂失效。

Deckard［3］发现，当橡胶管体发生局部异常变形时，管体会在短期内破裂失效。如何有效识别管体的局部异常变形，同时又能排除管体正常变形所带来的信号干扰，这是对橡胶管体寿命进行实时监测需要解决的难题。针对此问题，国内外许多学者开展了相关研究。例如，Emilio和Chevalierrm等［4-6］提出可以通过检测嵌入管壁的导线电阻变化来判断管体内部是否磨损；Maxwell［7］研究发现，将一种3层复合结构的变形感应装置植入管体内，通过检测其电学性质的变化可以判断管体是否失效；张洪娟等［8］提出了监测金属挠性接管变形的测点布置及数学模型。然而，对于FW-FP管体的变形检测方法研究存在2个方面的问题：一是内置传感器的布置设计要考虑到FW-FP管体的复合材料结构特性；二是针对管体不同变形状态，电阻检测原理是否适用、可靠。

鉴于此，本文将基于电阻检测理论，针对挠性接管的结构和变形特性，对传感器进行整体设计，建立基于传感器电路电流的阈值模型，并结合数值计算进行分析论证，以验证该方法检测管体变形的可行性，用以为评估FW-FP使用寿命时提供指导。

1 管体变形测量方法研究

1.1 电阻检测原理

Deckard在早期研究普通橡胶软管的寿命检测装置［3］时，提出将金属导线传感器埋入橡胶层内，通过检测金属导线电阻值的变化来反映管体橡胶层的变形量。如图1所示，管体分为3层，编号60表示整体结构模型，编号12表示内胶层，编号62表示单根缠绕在内胶层的金属导线，编号64为2根交叉螺旋缠绕在内胶层上的金属导线。

检测金属导线的电阻R由下式计算：

式中：ρ为金属导线电阻率；l为金属导线的长度；S为金属导线横截面积。

当管体产生变形时，在拉伸作用下金属导线的电阻值会发生变化，通过检测直流电流的变化可反推出管体变形量。

1.2 基于电阻测量原理的传感器设计

FW-FP挠性接管与普通的橡胶软管相比，它具有一层由多层凯夫拉纤维帘布缠绕的骨架层。凯夫拉纤维帘布由凯夫拉纤维通过化学处理后编织而成，骨架层一般包括4～6层帘布。凯夫拉纤维是一种高性能复合材料，其弹性模量与基体橡胶材料的弹性模量的比值约为105，导致管体的内压主要由骨架层来承受［9］，故可以将传感器嵌入骨架层中对管体变形进行检测。图2所示为传感器结构模型，金属导线按照一定的缠绕角度以螺旋方式缠绕在第3层凯夫拉帘布层上，通过金属—橡胶粘合剂将金属导线粘合固定在第3层与第4层凯夫拉帘布层之间，导线通过压紧法兰加工的小孔伸出与外部检测设备相连接。

图2 传感器结构Fig.2 The sensors configuration

图3所示为管体变形检测装置原理图。在与金属导线相连接的外接电路中，电源采用可调节直流电压电源，限流电阻主要用于保护电路。电流检测装置用于检测电路中的电流信号，电流信号经过软件处理后，得到电流变化量，通过对比系统设置的基准阈值来判断管体是否发生局部异常变形。

图3 检测装置原理Fig.3 Principle of the detection device

2 数学计算模型

2.1 初始状态传感器的电阻值分析

已知电流公式如下：

式中：I为通过电路的电流；U为电源电压。

将式（1）代入式（2），可得

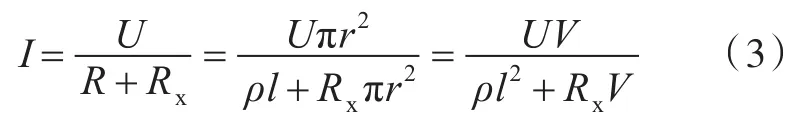
式中：Rx为限流电阻；r为金属导线横截面半径；V为金属导线体积。

金属导线按照一定的角度均匀缠绕在挠性接管的骨架层上。由于挠性接管是轴对称结构，可以选取挠性接管的对称中心作为原点建立柱坐标系［4］，如图4所示。

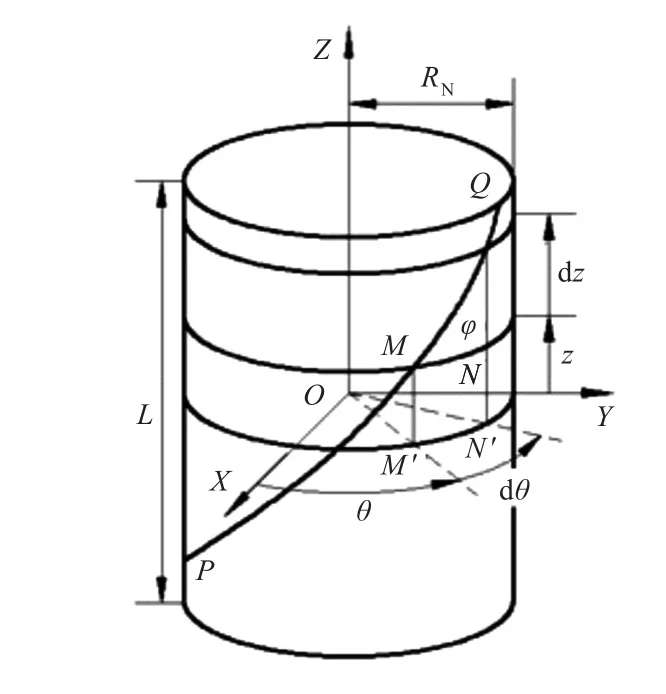
图4 金属导线缠绕模型Fig.4 The model of wire winding

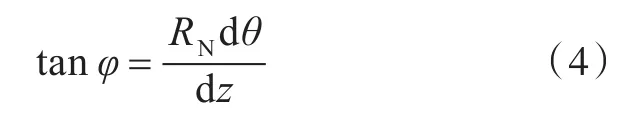
将式（4）代入式（5），取 z=L，积分得到该金属导线在直管上缠绕的长度l0：

将式（6）代入式（3）可得电流公式：

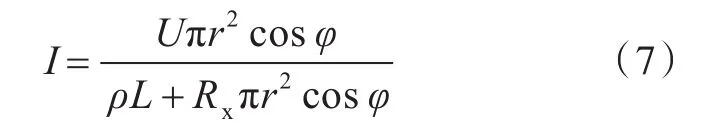
2.2 管体径向变形状态下传感器的电阻值分析

挠性接管在剪切力作用下会产生径向位移变形。假设一端为法兰固定，另一端法兰由于径向位移而发生偏移，选取一端法兰中心作为坐标原点建立坐标系，如图5所示。

图5 管体径向变形Fig.5 Radial deformation of the pipe body

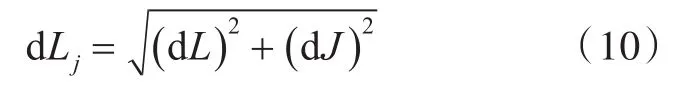
将式（10）代入式（9）积分可得

将式（11）代入式（6），可得管体在径向变形状态下金属导线的长度lJ为

在初始状态下，金属导线的体积V=l0·S=πr2L/cosφ。当发生变形后，V不变，代入式（3）中，可得到管体在径向变形状态下的电流值为

则 ΔIj=I-Ij，令 Z=πr2cosφ ，可得到管体在径向变形状态下电路的电流变化量ΔIj为

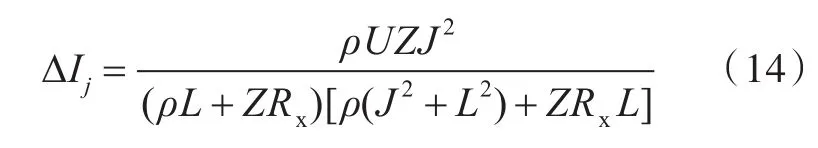
2.3 管体充压变形状态下传感器的电阻值分析

图6所示为管体在充压变形状态下的力学模型。金属导线螺旋缠绕在骨架层上，在充压作用下，导线沿长度方向的受力是均匀的。图中，QL为管体由于内部充压作用而在管壁上产生的纵向力，QR为环向力，F为螺旋导线在切线方向受到的力，p为导线缠绕的螺距，D为管体的直径［10］。

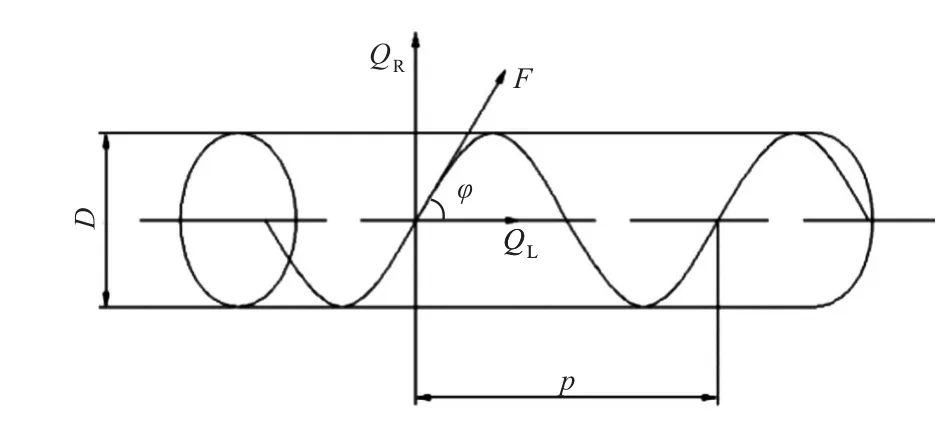
图6 管体充压状态Fig.6 Pressurized state of the pipe body

已知 QL=PD2π/4 ，QR=PDp/2 ，p=πD/tan φ（其中P为管壁承受的内压），由此推导可得

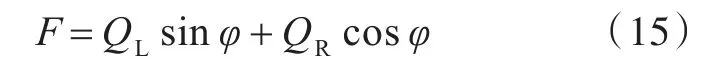
由弹性材料应力应变公式，可得到缠绕的金属导线的轴向变形量 ε［11］为

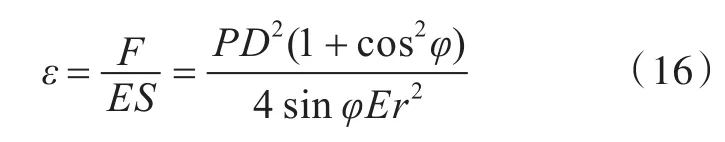
式中：E为金属导线的弹性模量。推导可得管体在充压变形状态下电路的电流变化量ΔIc为

2.4 管体局部异常变形状态下传感器的电阻值分析

如图7所示，设管体局部异常变形发生在管体的某一区段b，该区段沿管体轴向的长度为Lb。由于发生异常变形而使得应力集中，导致缠绕在该区段的金属导线横截面发生较大的径向变形量Δr，使金属导线横截面半径变为rb，其横截面积变为Sb，该区段的导线体积Vb不变。

图7 管体局部异常变形Fig.7 Local abnormal deformation of the pipe body

在产生局部变形前，缠绕在b区段管体部分的金属导线长度为lb'，未变形区段a缠绕的金属导线长度为la，则由式（6）可得

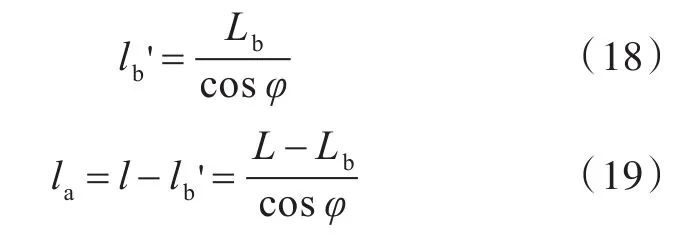
在发生局部变形后，缠绕在变形区段的金属导线长度变为lb，则可得

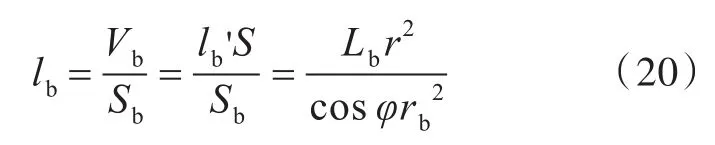
当管体发生局部异常变形时，变形区段的电阻发生改变，而其他未变形区段的电阻不变，两者为串联关系，则可得

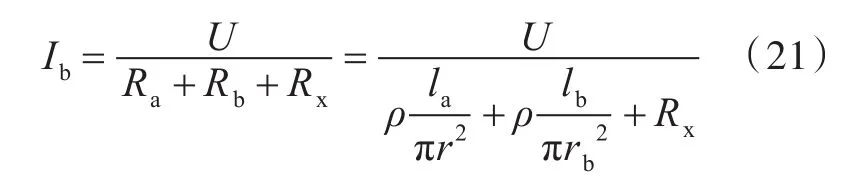
式中：Ib为管体发生局部异常变形后的电路电流；Ra为金属导线未变形区段的电阻值；Rb为金属导线变形区段的电阻值。

已知rb=r-Δr，推导可得电流变化量ΔIb：

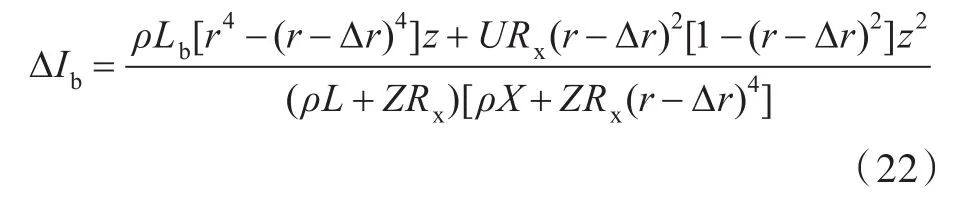
式中：X=(L-Lb)(r-Δr)4+Lbr4，X指关于 Lb，r，Δr，L的代数式。

3 数值计算分析

在数值计算时，选取典型的DN100挠性接管进行分析，缠绕的金属导线采用导电率较高、抗腐蚀性能强的铜线。固定参数如表1所示。

由于管体的3种变形状态是随工况变化的，而影响工况的3个变量为：一端法兰的偏移距离J；管壁承受的内压P；局部变形区段对应的导线径向变形量Δr。变量波动范围如表2所示。

表1 固定参数Table 1 Fixed parameters

表2 参数变化范围Table 2 Variation range of the parameters

将上述参数输入数学计算模型，分析3种变形状态的特性。

图8所示为管体在径向位移状态下，电流变化量随法兰偏移距离变化的曲线。由图可知，电流变化的范围为0～6.022×10-6μA，电流变化很小，可忽略不计。

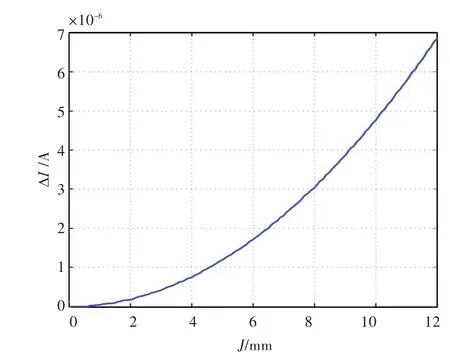
图8 径向变形状态下电流变化曲线Fig.8 Variation curve of current under axial deformation

图9所示为管体在充压变形状态下，电流变化量随压力变化的曲线。计算可得铜线的线应变的范围为0～0.135，代入图9中，则电流变化范围为0～20.2 mA，量级较小。说明这两类正常变形导致导线阻值变化很小，电流变化量级很小。

图9 充压变形状态下电流变化曲线Fig.9 Variation curve of current under inner deformation of pressure

图10所示为管体在局部变形状态下，电流变化量随变形区段金属导线径向变化的曲线。由图可知：在变形的初始阶段，当Δr=0～0.9mm时，ΔI随Δr变化较小，ΔI几乎为0；当管体发生较大的局部变形时，Δr=0.9～1 mm时，ΔI随 Δr变化较大；当 Δr=0.96 mm时，ΔI达到0.25A，这时管体产生的异常变形较大；当Δr=1 mm时，表明金属导线已被拉断，电路断路，ΔI达到极限最大值。将识别局部异常变形的电流阈值设定在0.25 A，可有效识别管体的局部异常变形，同时能排除正常变形带来的信号干扰。具体的分析数据如表3所示。

图10 局部异常变形状态下电流变化曲线Fig.10 Variation curve of current under local abnormal deformation

表3 管体3种变形状态下的分析结果Table 3 The analysis results of pipe body under three deformations

4 结 语

本文针对FW-FP挠性接管结构和变形特性，提出了一种基于电阻检测原理的管体变形检测方法。设计了埋入FW-FP骨架层的传感器结构模型，分析了基于3种不同管体变形状态下的电流变化特性，建立了电流阈值模型。通过对比实时反馈的电流信号和电流阈值，可以区分管体的局部异常变形和正常变形。通过对典型的DN100挠性管体的数值计算，验证了该管体变形检测方法的可行性，可为后续对FW-FP挠性接管的寿命评估提供依据。

下一步将开展传感器检测灵敏度、测量范围等方面的研究，并设计相关试验进行论证分析。