一种基于二维离散小波变换的边缘检测方法
2019-08-23米日班买吐地吐尔洪江阿布都克力木
文/米日班·买吐地 吐尔洪江·阿布都克力木
1 引言
图像边缘指的是信号的高频部分,一般对图像进行边缘检测其实检测信号的高频部分,它是灰度在图像上的突变。图像的这些突变点一般在图像的边界上,边缘检测就是找出这些突变点。边缘检测是数字图像处理和计算机视觉中的重要研究内容之一,它的目的是辨别图像中亮度变化明显的点。
目前,比较常用的传统图像边缘检测算法有:Sobel算子,Priwit算子,比较成熟的Canny算子和LOG算子等。虽然这些算子实时性良好,但对噪声很敏感,去除噪声能力也不理想,很多时候把噪声误取为边缘。Canny算子相对于其它传统的边缘检测算子,检查的边缘较准确,定位和效果比较好。
但如果选取的阈值不当,通常噪声淹没边缘信息。一般图像的边缘带着一些噪声,需要我们对这些噪声进行处理,但往往进行这个过程中,会发现,一些真正有用的边缘也跟着噪声丢失,检测出来的边缘信息不太完整。
为了更好的检测出图像的细节部分,可以利用图像增强算法来增强图像。目前图像增强的方法较多,其中直方图均衡化是被研究者广泛使用。直方图均衡操作是指对图像直方图进行处理,使得处理后的图像直方图为平坦形状。这方法在一定程度上降低了噪声对边缘提取和突出图像细节的影响,而且通过小波分解有效的去掉噪声,最终保留有用的,比较清晰的边缘信息,效果比传统的检测方法更好。
2 理论基础
2.1 二维离散小波分解原理
二维小波变换与一维小波变换一样从原信号开始在每层分解上一层的低频系数部分,每次分别对纵向和横向的信息分开处理,就生成了一组近似系数和三组细节系数。虽然这结果是很完美,但人们所追求的目标不止这些。研究者往往利用它对信号进行滤波或改变。换句话说就是,利用小波变换把一个信号分解成为各种不同频带的成分以后,并不是直接对这些成分进行重构,而是根据需求,对这些成分进行适当的改变,然后再利用这些改变以后的信号成分进行重构得到自己想要的结果。二维离散小波变换有快速算法叫Mallat算法过程图如图1所示。
Mallat算法使信号通过低通滤波器L后得到近似于原信号的数据;通过高通滤波器H后得到边缘细节信息的数据。
如下两个等式是小波分解算法:
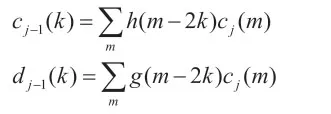
这两个公式是简化小波变换系数计算的关键。
2.2 直方图均衡化
直方图均衡化的大概思路是吧原图不均匀的直方图变为均匀的直方图,这样可以把灰度值的范围变大,可以使灰度均匀分布,增加反差,可以达到增强图像的目的。这样增强后的图像细节变得比原图更加清晰。在直方图连续的时候,直方图变换可以使用如下灰度变换公式,即:
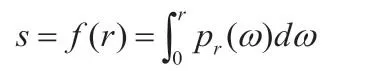
一般,在实际应用中,往往处理的是离散化后的图像,离散形式可以表示为:
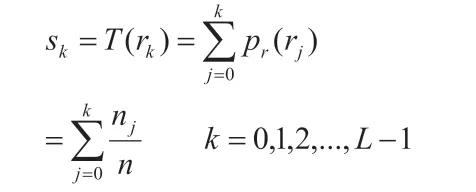
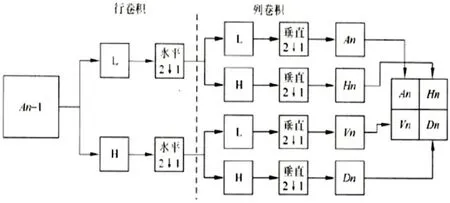
图1
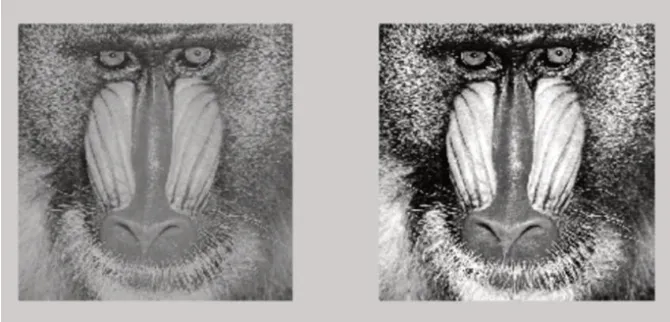
图2:原图baboon及图像增强后的图
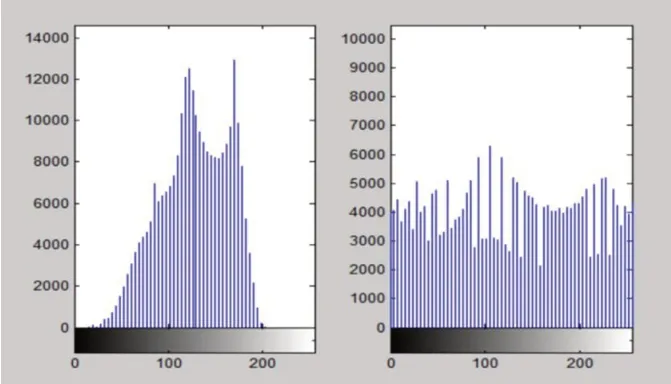
图3:原图直方图及均衡化直方图
其中,n为图像中的像素数目的总数,nk是灰度值为rk的像素数目,L为图像中可能的灰度值数目。利用上式可以把灰度值为rk的像素映射到相应的灰度值为sk的像素来实现均衡化。
3 实验结果与分析
本实验在matlabR2010a环境下进行,选取的图片是信息量较大的baboon图像(图2),其类型是bmp的512×512的灰度图。实验具体步骤如下:
第一步:首先对原图进行直方图均衡化来进行图像增强(图3);
第二步:对原图进行两次离散小波变换,得到图像的低频与高频部分,第一次去掉高频部分,从而达到去除图像中的噪声。
第三步:因为我们需要的边缘信息一般在图像的高频部分,接着把第二次的低频置为零,从而得到图像的边缘信息。
为了突出本文提出的边缘检测方法的优越性,对原图分别采用sobel算子和二维离散小波变换进行边缘检测,通过此方法得到的两幅图(图4和图5)与本文提出的方法得到的图(图6)进行比较。很显然,在三个实验结果中可以看到,用本文的方法得到的边缘信息更全,细节更清晰,检测出的边缘更完整连续。

图4:sobel算子边缘检测结果

图5:离散小波变换检测结果

图6:本文检测结果
