四阶带通式无源辐射器扬声器系统
2019-08-23周东宪郭清学
文/周东宪 郭清学
1 概述
带通式扬声器系统设计中普遍采用空气管来辅助低频辐射,但由于很多结构的限制导致空气管的使用有一定的局限性(如面积不可以很大,不可以很长等),尤其是在小型的扬声器系统设计过程中,这一局限性带来很多问题,如空气振动速度过快带来空气摩擦噪声等。因无源辐射器具有有效辐射面积较大,低频辐射失真低的优点,本文提出利用无源辐射器来作为四阶带通式扬声器系统的低频辐射器,取代空气管辅助低频辐射,对其系统函数加以分析,提出了具体的设计方法,并各相关参数的影响加以分析和讨论。
2 系统分析
箱体结构如图1所示,类比线路图如图2所示,这里忽略音圈电感的影响,同时不考虑信号源内阻。
根据图2的类比电路,可以建立精细的电路模型图3,其中Eg为信号源,Re为扬声器音圈直流阻,g=BL/Sd,BL为电-力变换因子,Sd为扬声器单元的有效辐射面积,Mas为扬声器的等效声质量,ras为扬声器振动系统的等效声导,Cas为扬声器的等效声顺,Cb1为Vb1腔空气声顺,Cb2为Vb2腔空气声顺,Cp为无源辐射器的等效声顺,Mp为无源辐射器的等效声质量,rp为无源辐射器的等效声导,等效声源Ps=gEg/Re,扬声器的总等效声阻Ra=g^2/Re+1/ras。根据图2和图3可以得到这类扬声器系统,阻抗频率响应函数Z(s)和声压频率响应函数P(s)为:

3 声压频率响应
3.1 系统传输函数分析
式(2)给出的声压频率响应函数为典型的四阶带通函数,其系统函数为:
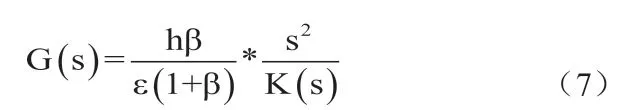
四阶带通响应的系统函数的一般形式如下:
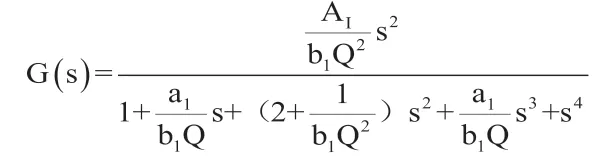
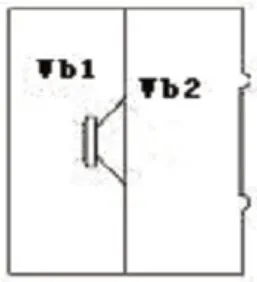
图1:箱体结构

图2:类比线路图
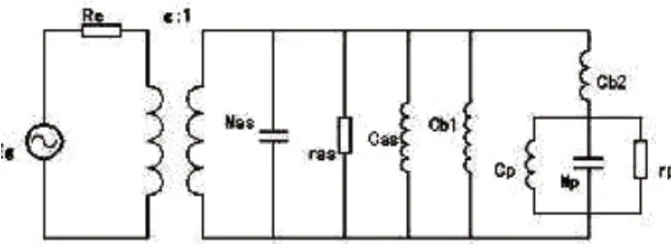
图3:类比线路图

由方程(8)可以看出a1、b1、Q、AI和β、γ、h、Qb、Qbp这五个独立的系统参数相对应,对于特定的响应,理论上可有多组系统参数满足设计要求。但系统参数之间的关系存在着很多限制,因此存在优化设计的问题。Qp为无源辐射器机械Q值,适当选取材料,可以认为其远大于Qb值,因此这里先视其为无穷大,则可解得:
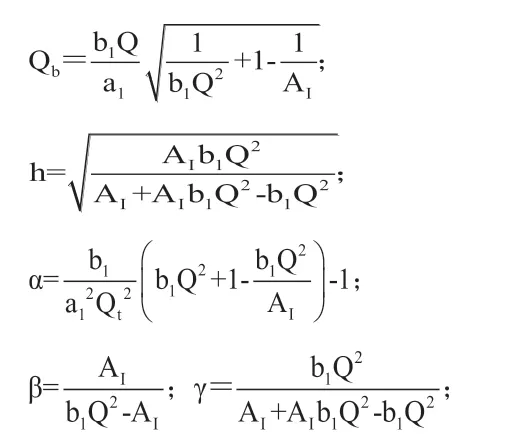
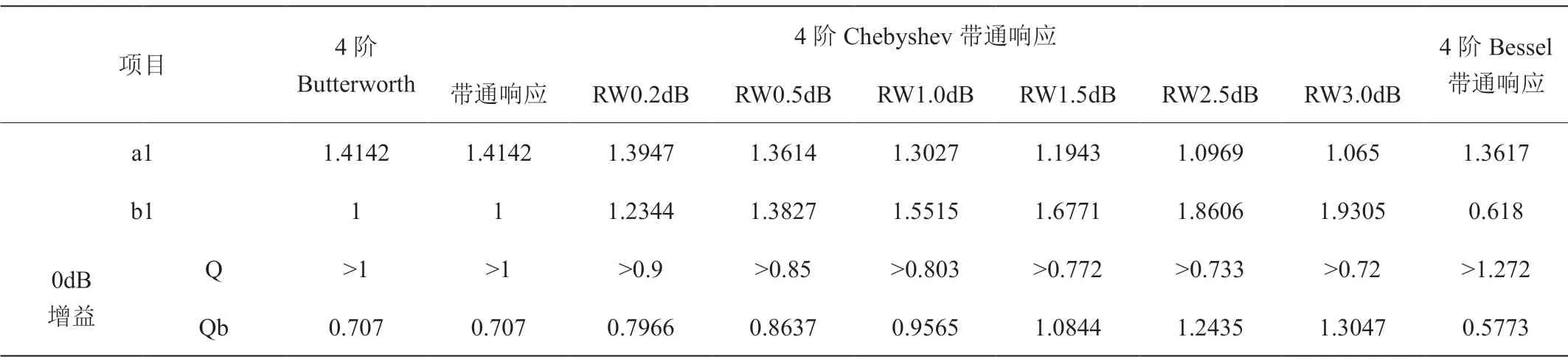
表1:典型响应的相关参数
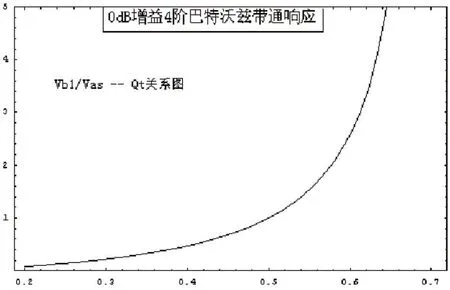
图4:0dB增益4阶巴特沃兹带通响应

图5:0dB增益4阶巴特沃兹响应

图6:0dB增益4阶巴特沃兹带通响应
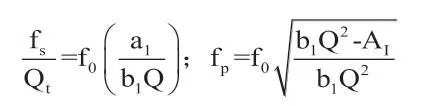
从上面的结果可以看出,箱体及无源辐射器相关的参数值为大于零的实数,上述结果才有物理意义。因此要有较高的增益,则意味着Q较高,也即频带变窄。对于0dB增益的系统Qb与至于a1和b1有关,与其他参数无关。附表1列出了几种典型响应的相关参数,对于特定的响应,AI、a1、b1是确定的,通带品质因子Q及通带中心频率f0是可以选择的,因此就带来了两种设计思路:
(1)对系统的通带特性提出要求(即确定通带的中心频率f0和通带品质因子Q)来选择合适的扬声器单元;
(2)根据特定的扬声器单元来设计合适响应,及其他系统参数(如无源辐射器参数和箱体参数)。不管采用哪种思路,至少必须预知f0和Q任意一个。
3.2 系统参数关系分析
可以看出,箱体参数、无源辐射器参数、扬声器单元参数和系统响应之间是相互关联的,有必要对它们之间的关系加以分析。
图4到图8是以增益为0dB的4阶巴特沃兹带通响应系统为例所进行的分析。
图4到图6反映箱体及无源辐射器容积参数Vb1、Vb2、Vp伴随扬声器单元的Qt变化关系图,伴随Qt升高,相应的容积参数有不同幅度的增加,如对箱体尺寸有要求,在设计过程中应该选择合适的Qt值。Qt确定,则对于特定响应系统而言,后腔的顺性比也是确定的,而前腔及无源辐射器的容积参数的确定,则需要考虑通带品质因子Q的要求,伴随Q的增加(通带变窄),Vb2及Vp将减小。
图7和图8反映的是系统中心频率f0和无源辐射器谐振频率fp与扬声器单元谐振频率fS的比值伴随Qt和Q变化的情况,可以看出伴随Qt的增加,f0、fp都逐渐降低,而通带品质因子Q的升高将导致f0、fp升高。
图9反映的是特定响应情况下扬声器参数和通带中心频率之间的关系,其中QLim为通带品质因子的极限值,可以看出,尽管Chebyshev响应的通带较宽,但其通带中心频率偏高,要满足相同的中心频率设计要求,Chebyshev的要求扬声器单元谐振频率fS和总品质因子Qt的比值较Butterworth和Bessel响应要低,要求扬声器单元有较低fS的和较高的Qt。Bessel响应虽然可是实现较低的中心频率,但其通带很窄。
3.3 0dB增益系统的设计
对于0dB增益系统有AI=1,得:

假设已知扬声器T/S参数为:Qt=0.45,Vas为2.65升,谐振频率为50Hz,设计4阶巴特沃兹带通0dB增益的系统,通带品质因子Q要求为为1.1,可求得:

响应模拟情况见图10所示。
3.4 非0dB增益系统的设计
非0dB增益系统,有AI≠1,此时各参数之间的关系表达式比较复杂,前文已给出相关的表达式,只要确定系统增益值,就可以根据给出的设计条件进行系统设计,当然也可以,根据系统参数的情况来计算系统增益情况,然后根据系统增益情况再来调整参数,如此错误尝试后,以得到合理或优化的系统响应。现在结合实例来对非0dB增益系统的设计进行分析,同前文一样,可有两种思路:
(1)根据扬声器单元设计特定的响应特性的扬声器系统;
(2)根据通带要求,选择扬声器参数,从而得出合适的箱体及无源辐射器参数。
例如要设计一系统增益为2dB的四阶巴特沃兹带通式扬声器系统,有a1=1.4141,b1=1,给出的扬声器TS参数同前文,同时根据系统增益可以得出Qb=0.805和Q>1.12,取Q=1.2,响应模拟情况见图11。
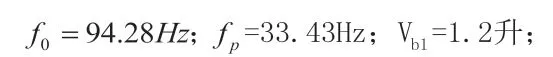
又例如要设计一系统增益为2dB,通带中心频率为80Hz,通带品质因子Q为1的四阶带通式扬声器系统,要求选择合适的扬声器单元,首先要确定的是a1和b1的值,因此必须选择合适的Qb,及a1和b1中任意一个值,取b1>Ai=1.259,取b1=1.3,得h=1.013,a1=1.382,可以知道fs/Qt=85,fp=14.3,其他参数与扬声器单元的参数选择有关。满足这样条件扬声器单元皆能满足,系统响应见图12。

图7:0dB增益4阶巴特沃兹带通响应

图8:0dB增益4阶巴特沃兹带通响应
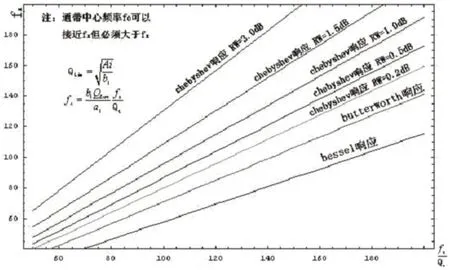
图9:扬声器Fs/Qt与通带响应关系
4 阻抗特性分析
设无源辐射机械品质因数为无穷大,即Qp为无穷大,结合前文分析,式(1)可简化为:

式(9)给出的阻抗频率响应函数和倒相箱的阻抗频率响应函数非常相似,阻抗频率响应曲线具有双峰的特性,如图13所示。第二项反映系统的动生阻抗,可以看出当f=f0时,阻抗有极小值。参照倒相箱阻抗函数的分析,不难看出阻抗频率函数中分子括号内实部为零时所对应的频率点处阻抗有极大值:
妻子起床去跳广场舞,闺女起床去上学,我依旧赖在被窝里睡懒觉。过去的早上,葱花油盐,紧张忙碌。现在的早上,鼾声缭绕,清闲安静。妻子跳舞回头,早饭顺手提回来。我赶紧地起床刷牙洗脸,吃罢早饭去上班。
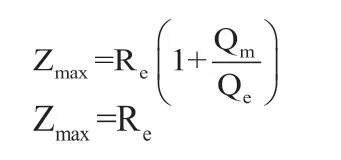

图10:响应模拟情况
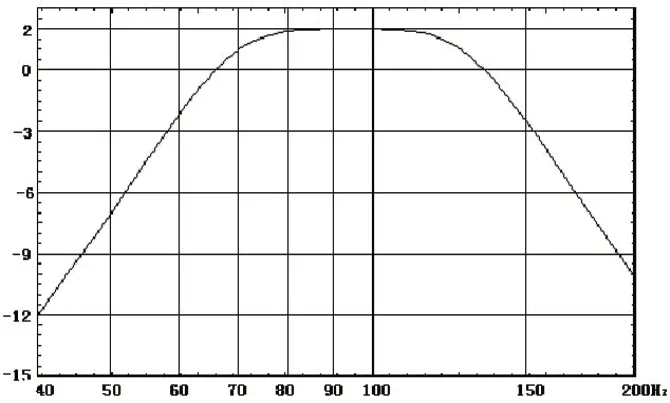
图11:响应模拟情况
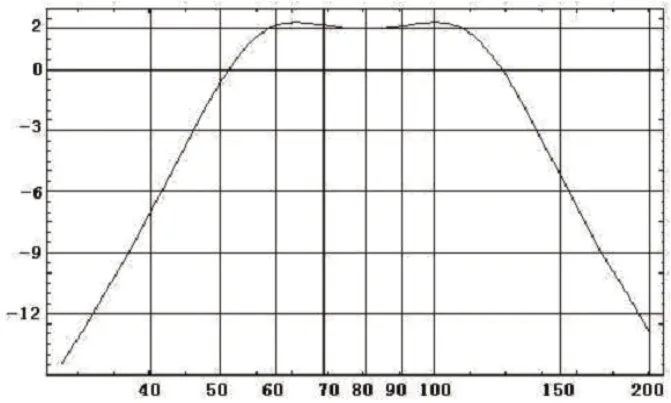
图12:系统响应

图13:阻抗频率响应曲线
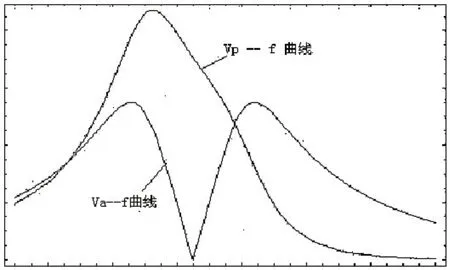
图14:速度响应曲线
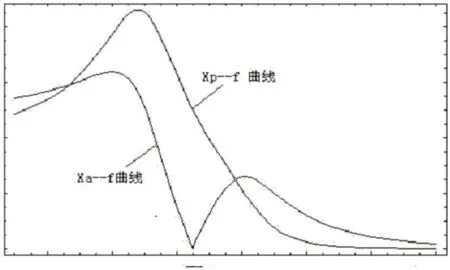
图15:位移响应曲线

图16:无源辐射器阻尼对频率影响

图17:无源辐射器阻尼对阻抗曲线影响

图18:图名无源辐射器阻尼对系统阻抗影响
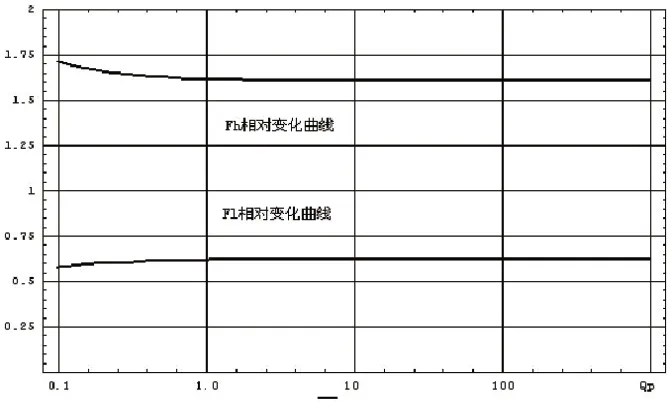
图19:无源辐射器阻尼对系统频率上限和下限影响

图20:无源辐射器阻尼对扬声器单元振幅影响

图21:无源辐射器阻尼对系统固有振动频率影响

5 速度和位移特性分析
不考虑Qp的影响即将其设为无穷大,由(3)到式(6)可得:

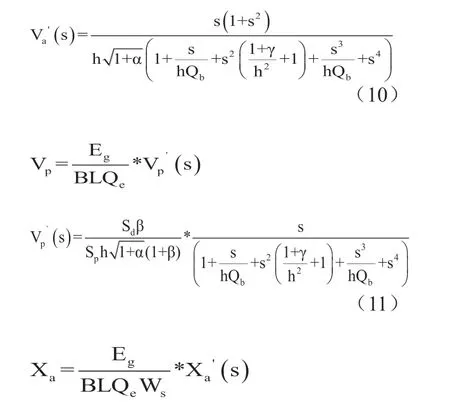
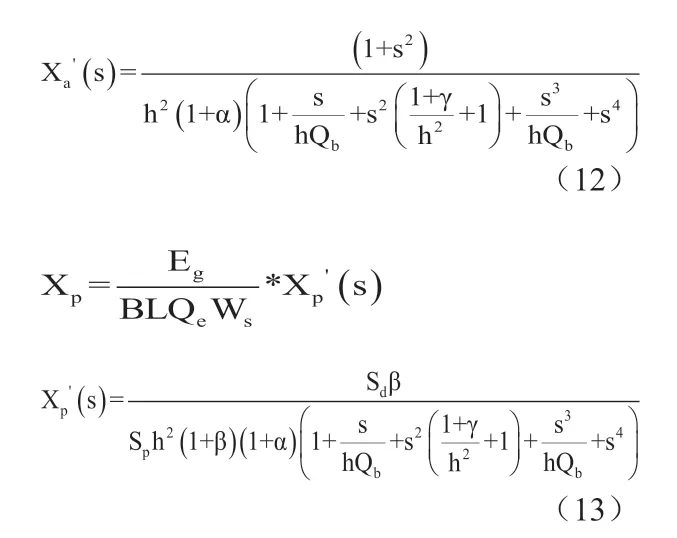
式(10)给出了扬声器单元的振动速度Va,不难看出当在频率等于f0处,扬声器单元的振动速度为零,由式(12)可以看出在此频率点扬声器单元的位移Xa也为零;在频率等于Fl和Fh处,扬声器单元的的振动速度有极大值为(EgQt)/(BLQe),该极值由扬声器单元本身的特性所决定,与箱体的参数无关;式(11)和式(13)为无源辐射器的振动速度和位移响应函数,可以看出其值与扬声器单元和无源辐射器的有效辐射面积比成正比,因此为了降低速度和减小位移量,通常应尽量提高降低面积比,无源辐射器的速度响应曲线见图14,无源辐射器位移响应曲线见图15所示。

图22:后腔容积变化对系统响应的影响
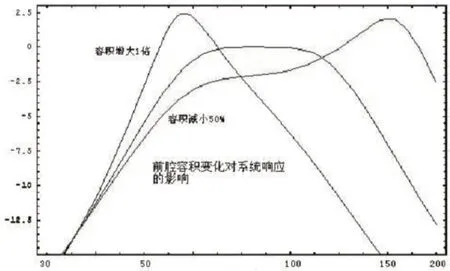
图23:前腔容积变化对系统响应的影响

图24:无源辐射器等效质量对系统响应的影响

图25:后腔容积变化对阻抗的影响

图26:前腔容积变化对阻抗的影响

图27:无源辐射器等效质量对阻抗的影响
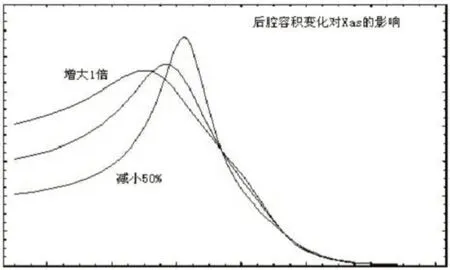
图28:后腔容积变化对Xas的影响

图29:后腔容积变化对Xas的影响

图31:前腔容积变化对Xps的影响

图32:无源辐射器等效质量对Xas的影响

图33:无源辐射器等效质量对Xps的影响
6 Qp的影响
前面的分析中假设了无源辐射器不存在阻尼的情况,实际上这种情况是不可能存在的,因此很有必要对其影响加以分析。
6.1 Qp对系统响应的影响
方程(8)给出了系统参数和Qp的关系,假设扬声器单元的TS参数同前文所述,无源辐射器的谐振频率为14.28Hz,等效容积为57.1升,箱体参数Vb1为10.1升,Vb2为2.03升,通过模拟情况来分析Qp变化对系统响应的影响。图16中曲线由低到高Qp的取值分别为1、2、3、5、10、20、无穷;为1/Qp频率-系统增益(dB)之间的关系图,可以看出Qp减小导致辐射效率降低,尤其对通带的低端影响更大,Qp大于10以后,影响在0.5dB以内,基本可以接受,这就要求在设计无源辐射器时,Qp值应控制在10以上,甚至更大。
6.2 Qp对阻抗响应的影响
图17显示的是阻抗频率响应曲线随Qp变化的情况,曲线由低到高Qp的取值分别为1、2、3、5、10、20、无穷;可以看出随着Qp降低,阻抗曲线的双峰不再对称,同时双峰有不同程度的降低,第一个峰低于第二个峰。
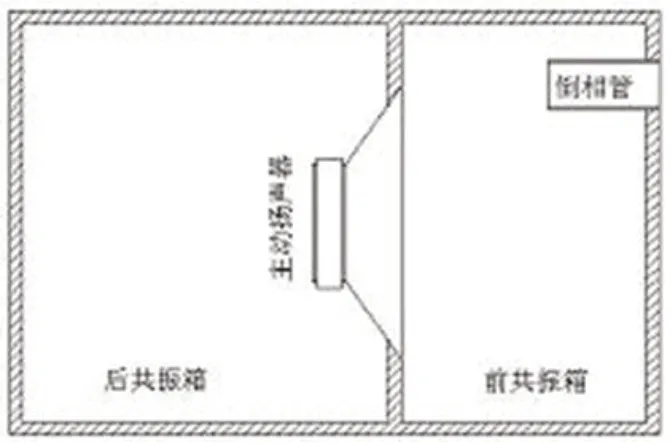
图34:传统四阶带通系统结构图
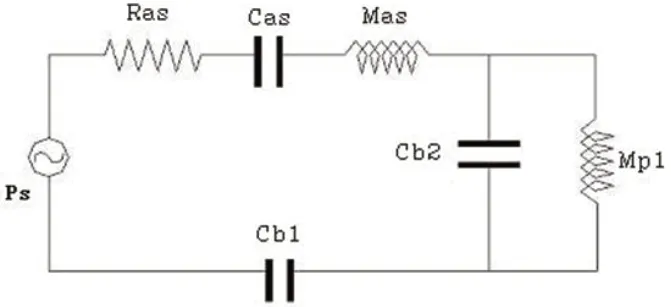
图35:声学类比线路图
见图18,同时阻抗极小值有所上升。因为阻尼伴随着Qp的降低而增加,必然导致声辐射能量损耗增加,从而声辐射效率的降低,尤其是在低端,这在前文已经验证。
有不同程度的降低,第一个峰低于第二个峰,见图18,同时阻抗极小值有所上升。因为阻尼伴随着Qp的降低而增加,必然导致声辐射能量损耗增加,从而声辐射效率的降低,尤其是在低端,这在前文已经验证。同时Qp降低导致阻抗曲线极值对应频点有轻微漂移,不是很明显。参见图19。
6.3 Qp对位移响应的影响
7 箱体及无源辐射器参数的影响
对于特定的响应和扬声器单元,箱体参数和无源辐射器的参数是确定的,但实际设计过程中经常需要根据实际情况对这些参数进行调整,因此有必要对此加以分析。
7.1 对系统响应的影响
图22反映的是后腔(Vb1)变化(其他参数不变)对系统响应产生的影响,可以看出后腔容积增大低频段向下有一定的延伸,但辐射效率降低,通带高端有所上升,衰减斜率变大;由图23可以看出前腔(Vb2)的增加,通带低端有一定的提升,但同时高端截止频率变低,同时通带边窄,容积减小时通带变宽,低端辐射效率下降,截止频率上升,高端辐射效率提高明显;图24反映无源辐射器等效辐射质量对系统响应的影响,可以看出无源辐射器的质量的增加主要影响通带的高端特性,对低端的影响主要表现在截止频率的向低漂移,而对高端影响出现了辐射效率的明显降低,而且相对变化较大,在设计过程中很有必要对这一参量加以叫严格的控制。
7.2 对阻抗响应的影响
参见图19。图25、图26、图27反映箱体及无源辐射器参数的变化对阻抗响应的影响,可以看出前后腔容积和无源辐射器参数的变化主要影响阻抗响应极值点变化,对阻抗值大小没有影响。
7.3 对位移响应的影响
后腔容积变化的影响主要集中在低频段,对于扬声器单元位移响应的影响相对较大(如图28和图29所示);前腔容积的变化对扬声器单元位移响应的影响主要在高频段,而对无源辐射器位移响应的影响主要在极值点附近(如图30和图31所示);无源辐射器等效辐射质量增大导致扬声器单元的位移响应最大值升高,最小值对应的频点下移,同时无源辐射器本声的位移响应最大值升高,其对应的频点下移(如图32和图33)。
8 和传统四阶带通系统的对比分析
传统四阶带通系统结构如图34所示,声学类比线路图如35所示。
图35中,Mp1为倒相管的等效声质量,其它参数如前文所定义。通过对图35的分析我们可以得出主动扬声器驱动空气的体积速度为:
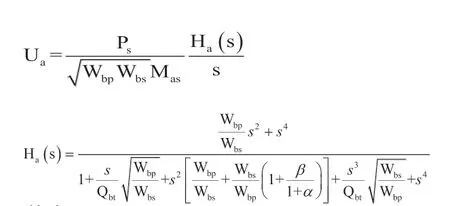
其中:
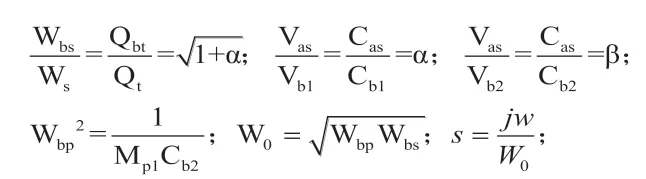
可得扬声器振膜的位移响应为:
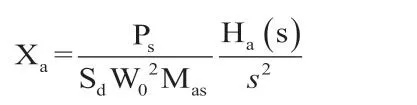
倒相管内的空气的振动速度为:

可知系统辐射声压为:

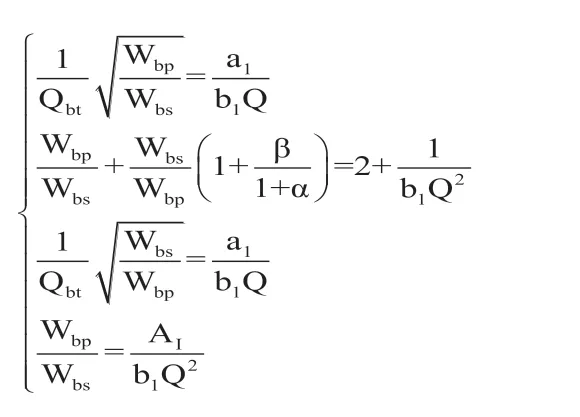
可解得: