汽车悬架振动系统的多目标优化设计

文/贾爱芹 宋辉 李玲

1 引言

现在人们越来越重视汽车的乘坐舒适性和操纵稳定性，而悬架对汽车的平顺性、操纵稳定性和乘坐舒适性等具有较大影响，因此对悬架系统优化设计至关重要。运用仿真手段对平顺性和操稳性进行优化，国内外在这方面已经开展了不少研究。本文建立1/2四自由度汽车悬架模型，结合方差和关联度的特点，用可靠灰色粒子群算法对其参数进行了多目标优化设计，来实现汽车悬架的多目标优化问题求解。

2 四自由度汽车悬架优化模型

以1/2车体为研究对象，建立4自由度系统学模型，建立其振动方程：

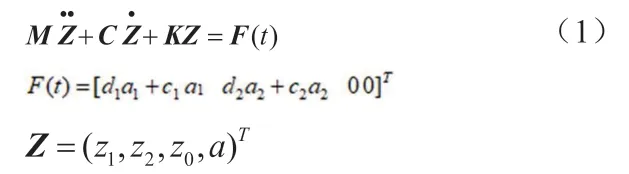
式中，D为刚度矩阵；C为阻尼矩阵。l、h—前、后轮距离；

m1、m2—转动惯量；I—轴的非簧载质量；m3—簧载质量；

z1(t)、z2(t)—前、后非簧载垂直位移；e0(t)—车身垂直位移；

d1、d2—前、后轮胎刚度；d3、d4—前、后悬架弹簧刚度；

c1、c2—前、后轮胎阻尼系数；c3、c4—前、后悬架阻尼系数；a1(t)、a2(t)—前、后轮激励。

3 悬架参数优化设计模

3.1 设计变量

3.2 约束条件

悬架的动挠度要被限制在一个安全范围内，一般要求

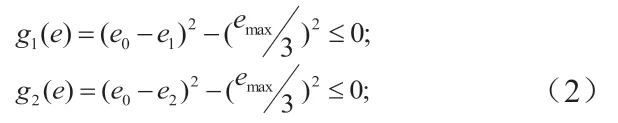
式中：e0-e1、e0-e2—前、后桥位移；emax—最大动挠度，一般取80mm。

3.3 目标函数

车体垂向加速度均方根值为：

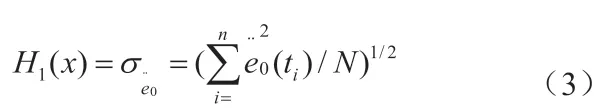
前、后轮胎对路面的瞬时动载荷分别为：

由于U1(t)和U2(t)均为随机载荷，则前、后轮胎动载荷的均方根值分别为：

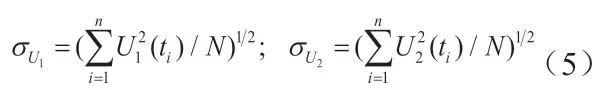
式中：N—采样数目。前、后轮均方根值为：

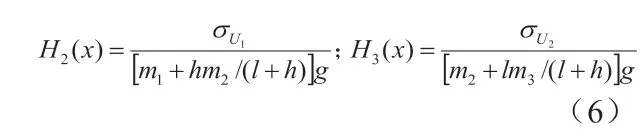
H1(x)、H2(x)、H3(x)为目标函数，g1(e)、g2(e)为约束条件。

4 可靠灰色粒子群优化算法

4.1 基本粒子群算法

标准PSO算法公式为：

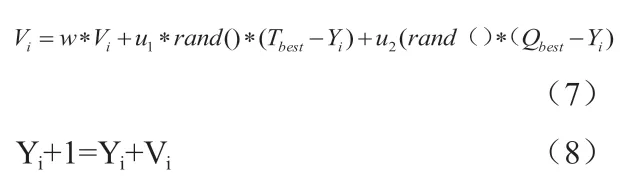
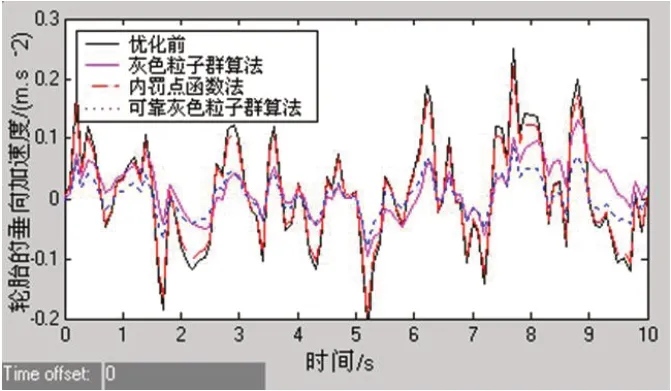
图1：车身垂向加速度均方根值仿真变化曲线

式中：i=1,2,…s，s—微粒的总数；Yi—粒子的当前位置；Vi—微粒的速度；ω—惯性权重；u1和u2—学习因子；Tbest、Qbest—个体极值和全局极值；rand()—随机数，rand()∈(0,1)；Yi=(x1,x2,…,xs)、Vi=(v1,v2,…,vs)—粒子在S维空间中的位置和速度。

4.2 可靠灰色关联度

（1）计算关联度

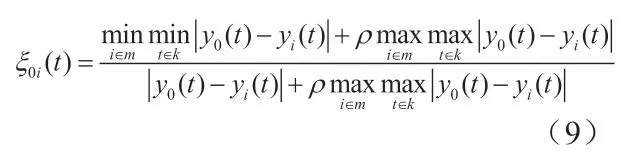
式中，ρ为分辨系数，，通常取ρ=0.5。

（2）计算平均关联度：

关联系数序列的方差为：

（3）计算可靠灰色关联度：

4.3 可靠灰色粒子群算法

（1）求F1(x)、F2(x)和F3(x)在约束条件式（3）下的最优值组成基准矢量序列：

（2）初始化Yi、Vi，代入式（5）、（8），得目标矢量序列：

（3）求Yi可靠关联度，比较大小，求出Tb和Qb；

（4）用式（8）、（14）、（15）更新各粒子的w、Vi及Yi；

（5）选最优Yi及其对应R0i，并将R0i和Yi存储在Tb中，比较Tb、Qb，更新Qb；

表1：变量取值范围

表2：悬架结构参数

表3：悬架参数优化结果

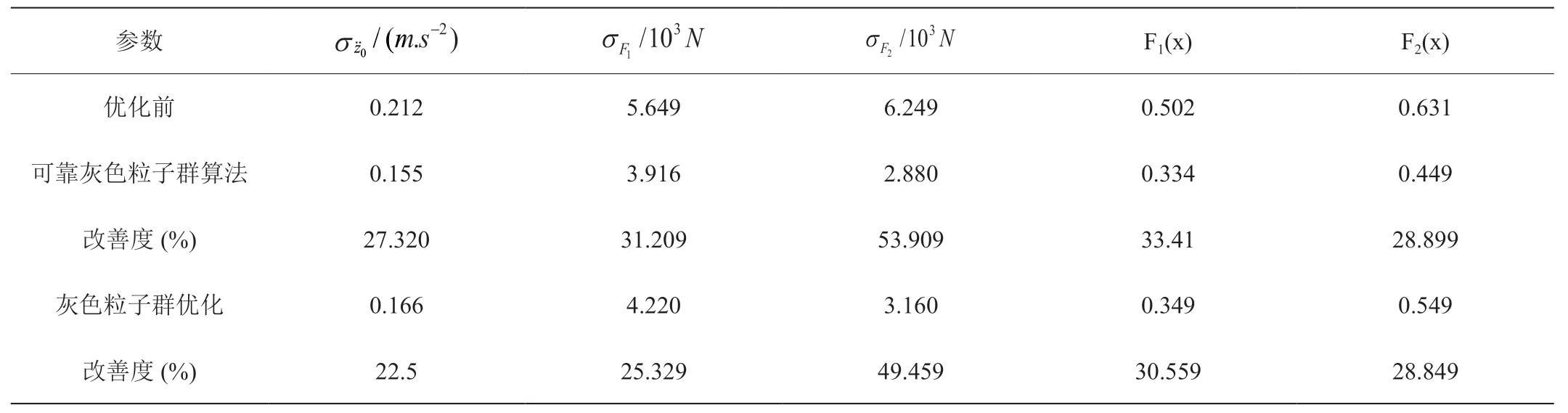
表4：车身垂向加速度和前、后轮动载系数均方根值优化结果

（6）若条件满足停止搜索，选最大的Yi及对应的粒子作为结果输出，否则，返回（4）。

5 算例结果与分析

以某10t载货汽车为例。令a=3.0m，b=2.6m，a、b—前、后桥至质心的距离，其它参数见表2。设货车行驶在B级路面，速度为28.00m/s。

利用不同的优化算法得到的优化结果见表3。

由表3知，k减少，c增大，且前悬架参数k3变化比后悬架参数k4变化小，使悬架系统性能变好。

表4为不同算法下 、 、 、F1、F2优化前后结果。 —车身垂向加速度、前后轮胎动载荷和前、后轮胎动载系数均方根值。

由表4知，两种不同的优化方法都使车身有不同程度的改善，提高了乘坐的舒适性。

利用matlab/simulin软件对该模型在时域内进行仿真，结果如图1。由仿真结果也验证以上结论的正确性。

6 结论

利用可靠灰色粒子群算法实现汽车悬架系统多目标优化模型求解。通过优化不仅可以提高车辆的舒适性，还可以减小重型载货汽车对路面的动载，减轻对路面的损伤。