基于序列二次规划法的导弹鸭舵/尾舵复合控制技术研究
2019-08-23黄鲁豫徐胜利张明环
黄鲁豫,徐胜利,张明环
(1. 西北工业大学航天学院,陕西 西安 710072;2. 上海机电工程研究所,上海 201109)
0 引 言
未来的空中威胁具有高速、高隐身、宽空域以及高机动特征,这些特征对下一代拦截弹的设计提出了严峻的挑战,需要其适应大范围的空域及速域的变化。与现役导弹相比,下一代导弹的作战高度需求更高,甚至要求其在20~30 km执行任务。在此环境下,由于空气非常稀薄,导弹气动舵控效率很低,舵容易处于饱和状态。如继续采用传统的控制方式,导弹在20 km以上高度飞行时已基本不具备过载能力,无法满足快速响应、大机动能力的任务需求[1-3]。
目前,国内外针对该问题的解决方案集中于采用气动力/直接力的复合控制方式,以期提升导弹的响应速度和机动能力[4-7]。与单纯依靠气动力控制相比,采用复合控制方式的导弹过载响应上升时间下降了一个数量级,而且可用过载的大小不受导弹飞行高度的影响,因此能够在很大程度上提高导弹控制系统的性能。
虽然气动力/直接力的复合控制方式是提升导弹控制能力的一种有效手段,但其代价是要在导弹上增加额外的能源,不仅增加全弹重量,还会挤压有效载荷的空间。针对该问题,本文提出了一种新的解决思路,通过增加一组鸭舵来增加导弹在高空时的可用过载,并设计了一种鸭舵/尾舵复合控制方法以保证导弹在全飞行空域和速域都具备快速响应和大机动过载的能力。
1 导弹建模
1.1 六自由度模型
本文假定的导弹气动外形如图1所示。导弹采用轴对称外形,安装有4片鸭舵和4片尾舵。俯仰通道和偏航通道采用鸭舵、尾舵联合控制,滚转通道由尾舵控制。
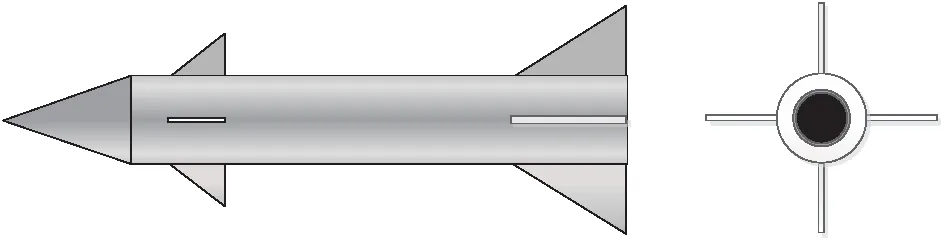
图1 导弹气动外形Fig.1 The aerodynamic shape of missile
为简化弹体动力学模型,把导弹视为刚体,暂时忽略地球自转的影响。导弹的六自由度模型如式(1)~(4)所示。
(1)
(2)
(3)
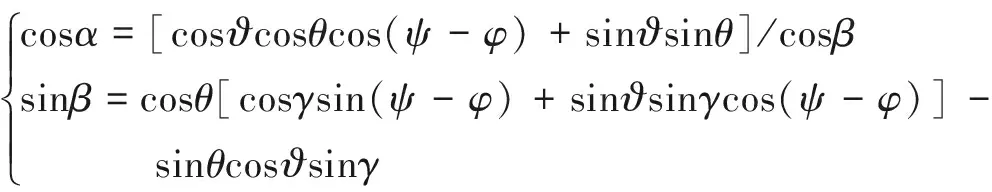
(4)
式中:ωx,ωy,ωz为三个姿态角速度;Mx,My,Mz为3个方向的力矩;Jx,Jy,Jz为3个转动惯量;x,y,z为发射系下导弹的位置坐标点;v为导弹飞行速度;θ,φ为弹道倾角和弹道偏角;ϑ,ψ,γ为俯仰角、偏航角和滚转角;α,β为攻角和侧滑角。
1.2 线性化数学模型
对轴对称导弹数学模型进行小扰动线性化,简化条件为:
1) 采用系数冻结法,即弹道上某一时刻t的导弹飞行速度v、高度H、推力P、质量m、转动惯量J均不变。
2) 攻角α、侧滑角β均为小量,即sinα≈α、cosα≈1、sinβ≈β、cosβ≈1。
3) 控制系统保证实现滚转角稳定,并有足够的快速性。
由此,导弹动力学模型可线性化为
(5)
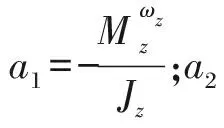
忽略运动学耦合项-ωxβ,可得导弹纵向通道小扰动线性化模型为
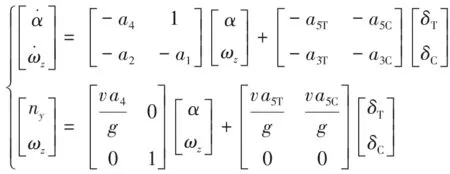
(6)
式中:ny为导弹法向过载;g为重力加速度。
同理,可得导弹横侧向小扰动线性化模型为
(7)
(8)
式中:nz为导弹侧向过载。
2 鸭舵/尾舵复合控制算法
以纵向通道为例,导弹鸭舵/尾舵复合控制系统结构如图2所示。

注: nyc为法向过载指令;Kny、Kα、Kω为三回路的控制增益系数;δzc为z通道舵偏控制指令;为积分环节;ωz(s)、δz(s)、ny(s)、α(s)分别为ωz(t)、δz(t)、ny(t)、α(t)经拉斯变换后得到的频域信号。图2 鸭舵/尾舵复合控制系统结构Fig.2 The canard/tail rudder compound control system structure
俯仰通道舵指令分配方式为
(9)
式中:Kz1,Kz2分别为鸭舵和尾舵的分配系数。
通过规划鸭舵/尾舵的分配系数(Kz1,Kz2),可以使作用于导弹的阻力最小化,从而保证导弹的高空过载能力。本文在过载三回路控制系统的基础上,采用序列二次规划法对鸭舵/尾舵分配系数进行以下优化设计,使得
(10)
式中:Cd为阻力系数。
(11)
3 序列二次规划算法原理
一般非线性约束的数学规划问题是[8-9]:
minf(X)
(12)
式中:X∈Rn是决策变量;f(X)是目标函数;gu(X)和hv(X)分别是不等式约束函数和等式约束函数。
利用泰勒展开把非线性约束问题式(12)的目标函数在迭代点Xk简化成二次函数,把约束函数简化成线性函数后得到的就是如式(13)所示的二次规划问题。
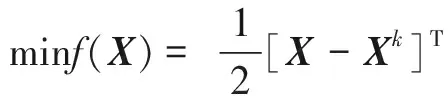
(13)
此问题是原约束最优化问题的近似问题,但其解不一定是原问题的可行点。为此,令S=X-Xk,将上述二次规划问题变成关于变量S的问题,即为

(14)
令H=2f(Xk)
C=f(Xk)
Aeq=[h1(Xk),h2(Xk),…,hm(Xk)]T
A=[g1(Xk),g2(Xk),…,gp(Xk)]T
Beq=[h1(Xk),h2(Xk),…,hm(Xk)]T
B=[g1(Xk),g2(Xk),…,gp(Xk)]T
(15)
将式(14)变成二次规划问题的一般形式,即为
(16)
求解此二次规划问题,将其最优解S*作为原问题的下一个搜索方向Sk,并在该方向上进行原约束问题目标函数的约束一维搜索,即可得到原约束问题的一个近似解Xk+1。反复迭代该过程,直至求得最优解。
4 仿真验证
为验证本文控制算法的有效性,构建以下仿真场景。
1) 目标从350 km外进入战区,侧向偏差z=100 m,飞行速度为1 800 m/s,飞行高度为30 km,在距离导弹70 km 时以3g过载做侧向机动进行规避,机动时间5 s。
2) 导弹以70°俯仰角从地面发射,爬升至近30 km高度后对目标进行跟踪拦截。
3) 仿真环境为Matlab/Simulink,仿真步长为0.001 s。
仿真结果如图3~11所示。

图3 纵向平面飞行弹道Fig.3 The trajectory in longitudinal plane
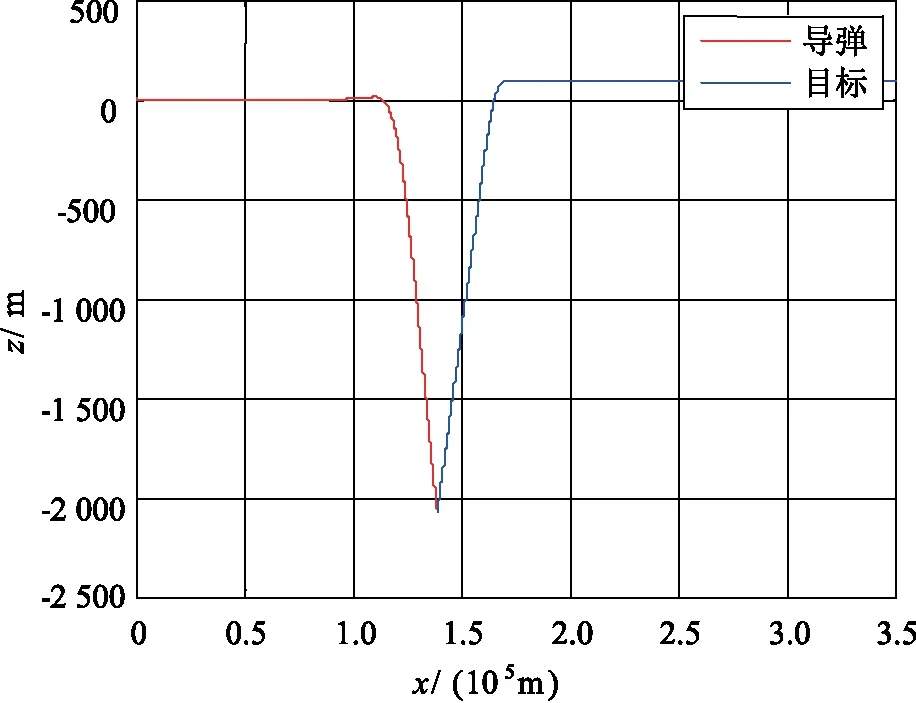
图4 横侧向平面飞行弹道Fig.4 The trajectory in horizontal plane
从图3和图4可以看出,在30 km的高空,导弹击中了目标,脱靶量小于3 m。

图5 导弹高度曲线Fig.5 The height curve of missile
从图5可以看出,导弹爬升至30 km后,姿态和轨迹能够迅速稳定收敛,证明了本文控制算法具有良好的动态特性和稳态特性。
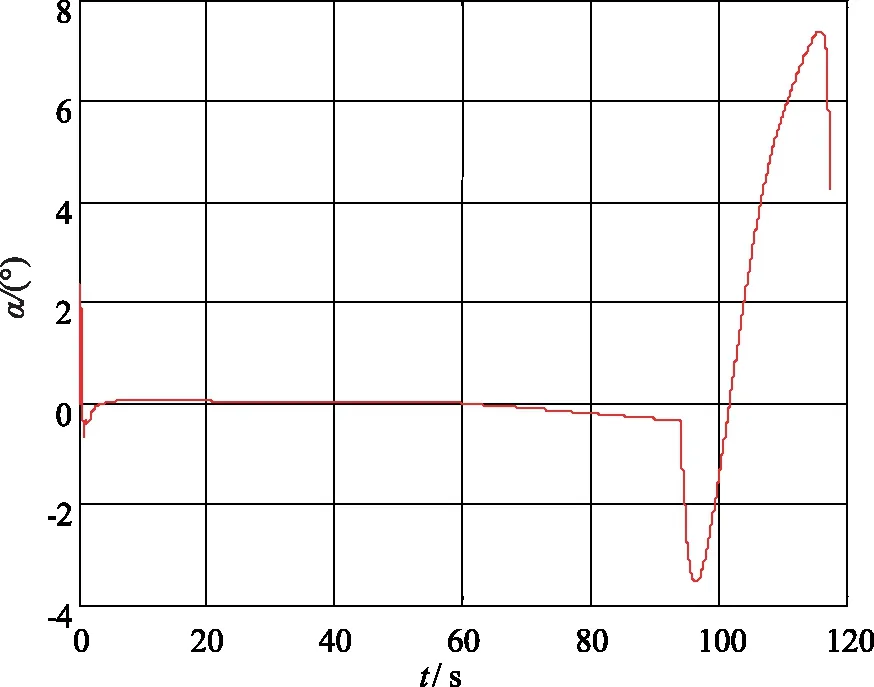
图6 导弹攻角曲线Fig.6 The attack angle curve of missile
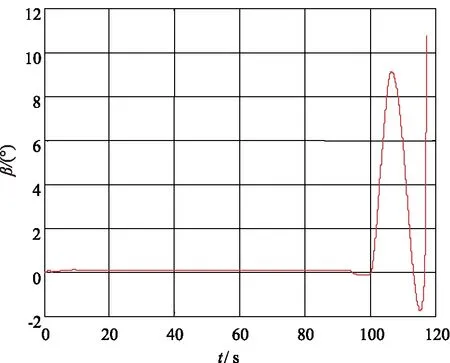
图7 导弹侧滑角曲线Fig.7 The sideslip angle curve of missile
从图6和图7可以看出,导弹在做机动时,攻角和侧滑角始终处于较小的状态。
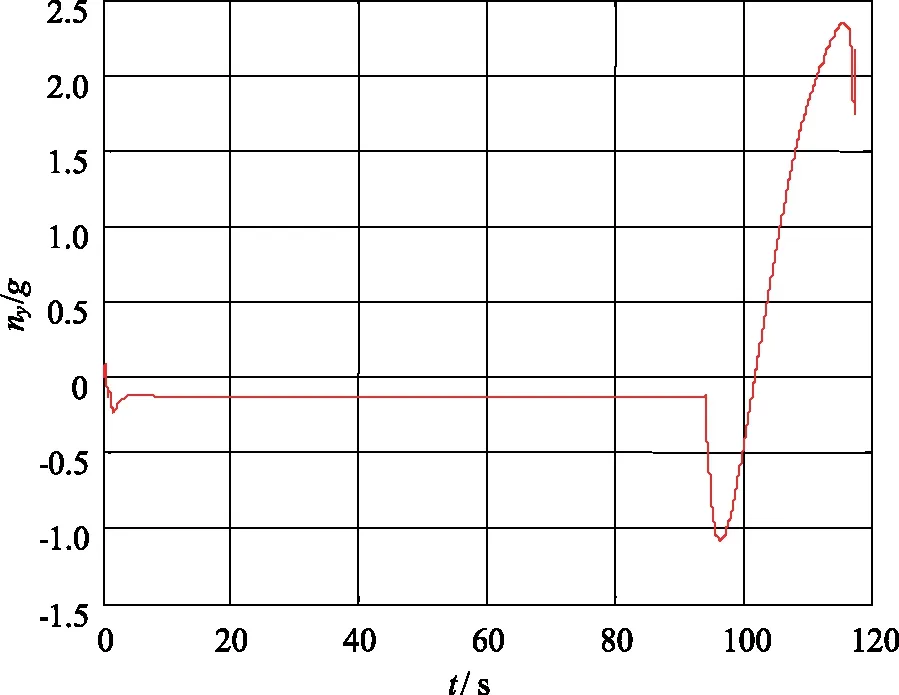
图8 导弹法向过载曲线Fig.8 The normal overload curve of missile
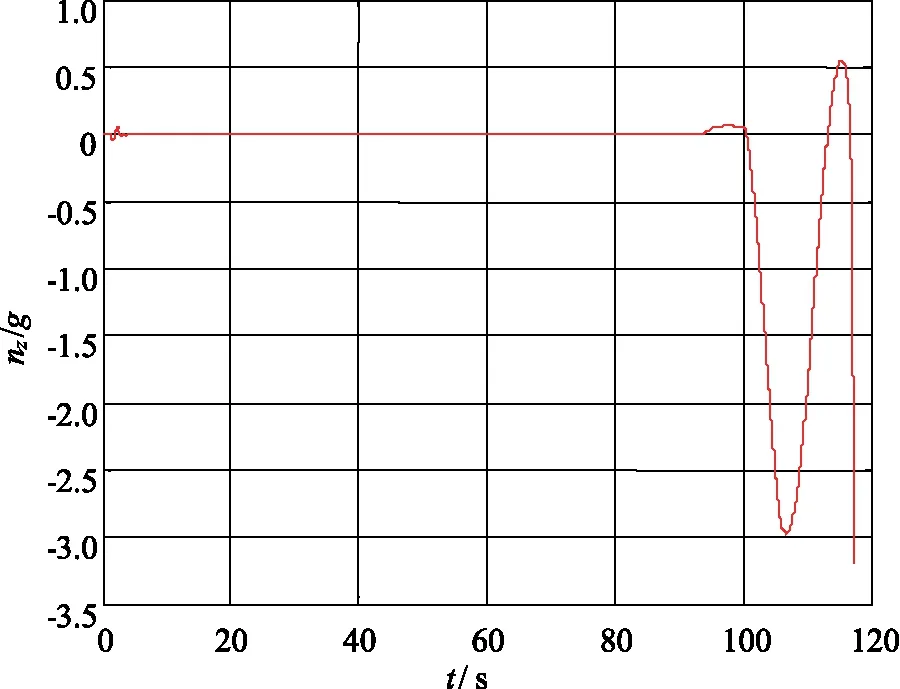
图9 导弹侧向过载曲线Fig.9 The lateral overload curve of missile
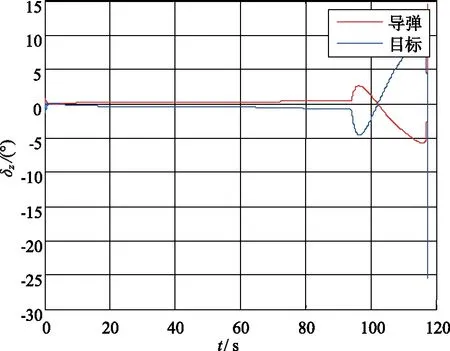
图10 导弹俯仰通道舵偏角曲线Fig.10 The pitching channel rudder deflection angle curve of missile
从图8和图9可以看出,在30 km的高空,导弹仍然具备3g以上的过载机动能力,证明了本文基于序列二次规划法设计的鸭舵/尾舵复合控制策略能够保证导弹的高空机动能力。
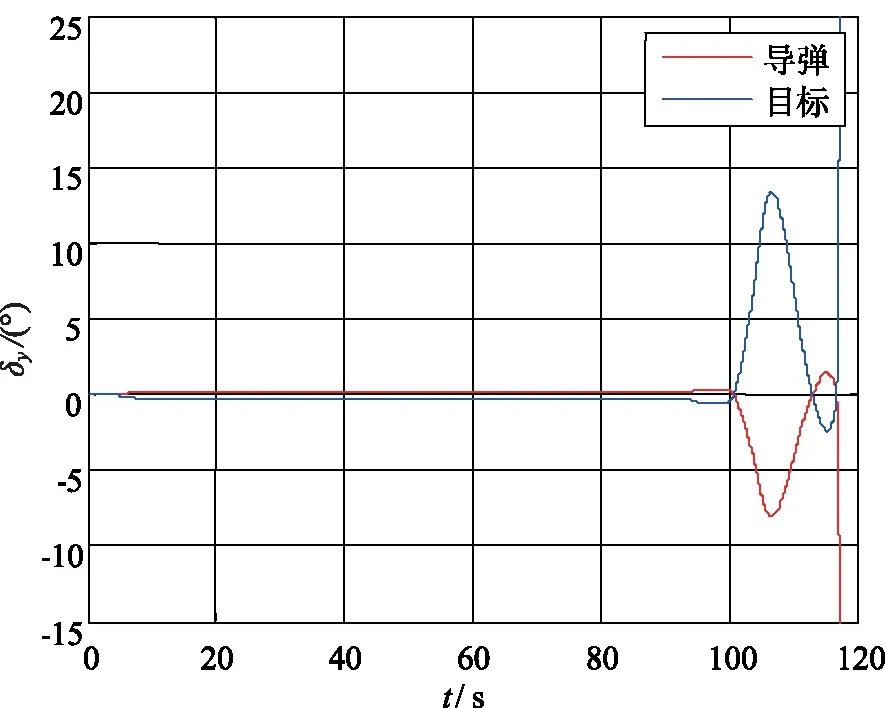
图11 导弹偏航通道舵偏角曲线Fig.11 The yaw channel rudder deflection angle curve of missile
从图10和图11可以看出,在30 km的高空,导弹在做3g的机动时,舵偏角小于15°,相对飞行器通常采用的25°限幅值仍有一定空间,表明导弹具备潜在的更大的机动能力,也进一步证明了本文算法的有效性。
5 结束语
本文设计了导弹鸭舵 / 尾舵复合控制系统,并采用序列二次规划法对鸭舵 / 尾舵的舵指令分配策略进
行了优化设计。通过仿真验证,证明了本文所设计的控制系统不但具有良好的动态特性和稳态特性,还能够保证导弹在高空仍具备高机动能力。本文的研究为未来导弹的设计提供了一种新的思路,具有较高的应用价值和工程意义。
