基于防止塑性垮塌的多晶硅还原炉底盘结构安全性评估

2019-08-22

压力容器 2019年7期

(华东理工大学机械与动力工程学院，上海 200237)

0 引言

还原炉是多晶硅生产的核心设备，其结构完整性关系着多晶硅的安全生产[1-3]。在还原炉设备中，底盘是主要的受载区域之一。由于底盘上设置进出口以及电极座，局部区域存在显著的应力应变集中。同时，该区域承载着设备的重量、压力等载荷工况，这使得局部受载状况更为复杂。因此，为保障还原炉的安全运行，有必要对还原炉底盘进行应力评定。

在以往的研究中，部分学者对底盘开展了温度场分析、流场计算等工作。例如，王晓静等[4-5]以24对棒多晶硅还原炉底盘为研究对象，利用Fluent模拟了底盘区域的流场，分析了底盘温度的均匀性，结果发现，冷却液的进口流量影响了底盘温度场的均匀性；周阳等[6-7]对还原炉底盘结构进行改进，并采用Fluent对底盘结构的温度场进行了模拟，结果发现，采用新型底盘结构后，其温度均匀性大幅提高。总的来讲，现有研究更多关注该区域的流场和温度场行为，但对还原炉底盘的强度评价关注较少。因此，还需要开展还原炉底盘的强度评价研究，以保障还原炉的安全稳定运行。

国内外规范中，均给出了部件强度评价的分析设计方法，包括国内的JB 4732[8]以及美国ASME Ⅷ-2[9]规范。以ASME Ⅷ-2为例，为防止塑性垮塌，提出了3种分析设计方法：弹性应力分析法、极限载荷法以及弹塑性分析法。弹性应力分析法采用弹性方法，对结构中的总应力进行分类，并将相应的应力限制在许用值以内；极限载荷法采用理想弹塑性材料模型，并基于小位移理论求解结构的承载能力；而弹塑性分析法考虑材料的非线性行为，评估结构的塑性承载能力。考虑到现有研究多基于弹性应力分析法进行部件的强度评价，本文研究将以某还原炉底盘为例，系统开展多种应力分析设计方法(包括弹性应力分析法、极限载荷法以及弹塑性分析法)的比较研究。

本文采用有限元软件ANSYS，以某36对棒还原炉底盘为例，开展不同应力分析设计方法的比较研究，包括弹性应力分析法、极限载荷法以及弹塑性分析法，并分析不同方法强度裕量的差异。

1 有限元模型

1.1 几何模型和材料参数

计算所用结构为某36对棒多晶硅还原炉反应器底盘的支撑结构，包括上底板、下底板、进气口、出气口、电极座、法兰及裙座。该结构主要设计参数为：设计温度330 ℃，上底板承受筒体内部压力0.65 MPa，夹套内承受压力0.6 MPa，电极座承受硅棒重量120 kg。由于该底盘支撑结构为轴对称结构，且在设计工况下承受的载荷也为轴对称，因此建立实际结构的1/4模型进行应力计算，其模型见图1。

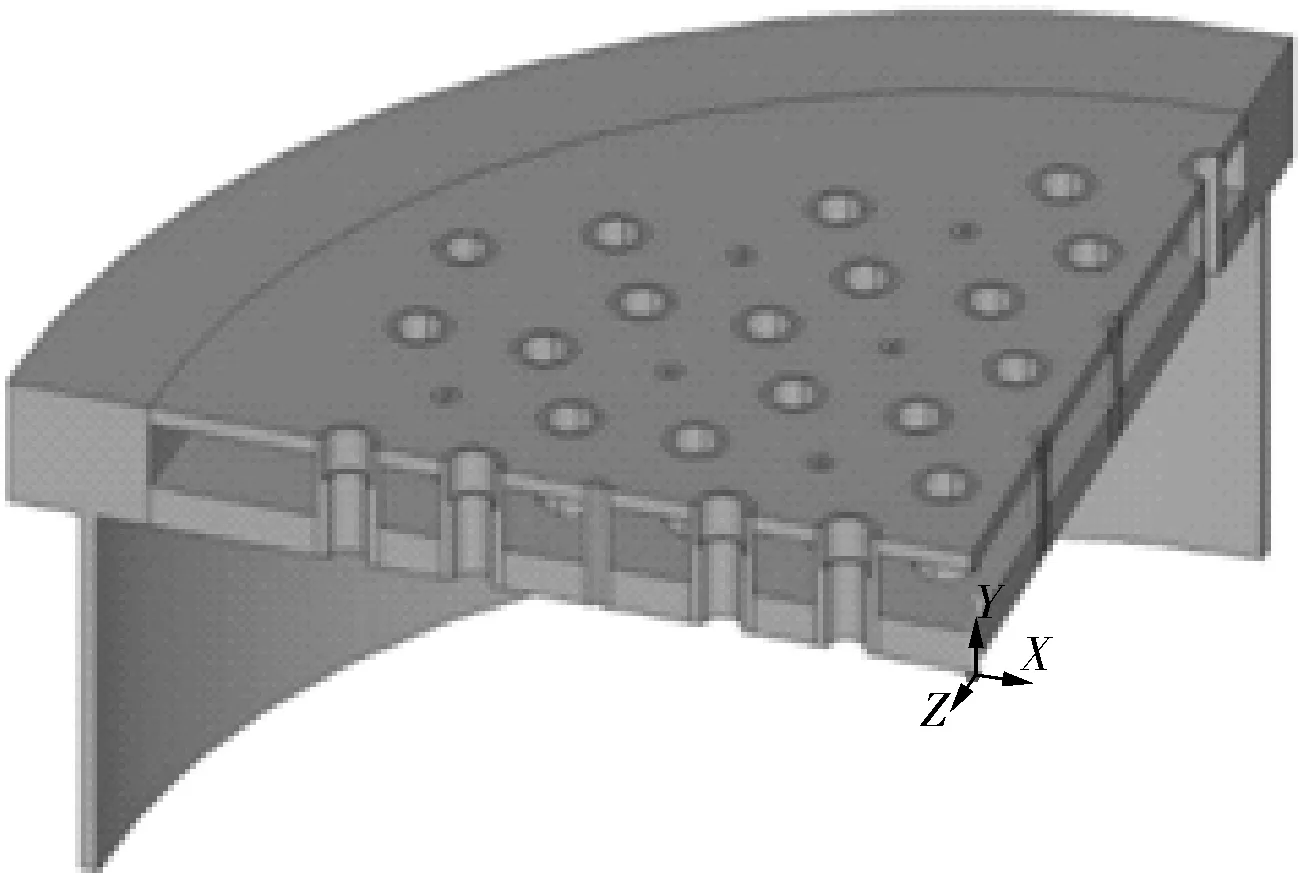
图1 底盘支撑结构的1/4模型

还原炉底盘支撑结构各材料的许用应力以及弹性模量等力学性能参数由GB 150—2011《压力容器》[10]查取，并利用插值法计算许用应力以及弹性模量等参数，如表1所示。

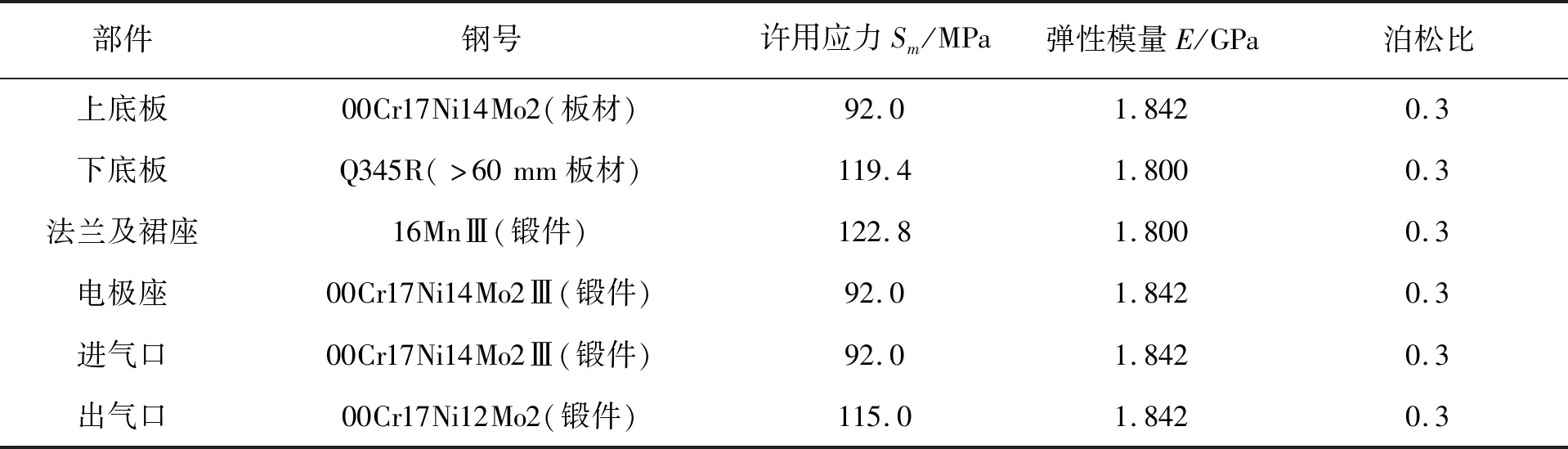
表1 材料力学性能及许用应力(330 ℃)

1.2 单元选择及网格划分

建立1/4轴对称模型，选择20节点的等参单元Solid 186单元进行网格划分，有限元网格模型如图2所示。经过试算确定了网格尺寸，最终的单元总数为116 515，节点总数为546 402。

图2 有限元网格模型

1.3 边界条件

根据实际的设计工况，该模型的边界条件如图3所示，主要包括如下内容。

(1)分别在X=0,Z=0的剖切面(即对称面)施加轴对称约束。

(2)在裙座下表面的圆环面上施加全约束。

(3)在上底板上表面施加压力载荷0.65 MPa。

(4)在上下底板之间的所有内壁面上施加压力载荷0.6 MPa。

(5)在电极座内支架的圆环面施加等效应力，计算公式如下：

(1)

式中M——硅棒质量，kg；

d1，d2——电极座内部圆环面的外径和内径，mm。

(6)在法兰下表面裙座边缘圆环面施加等效应力，计算公式如下：

(2)

式中P——筒体内部的压力，MPa；

D1——筒体内径，mm；

D2——法兰外径，mm；

D3——裙座外径，mm。

(7)考虑底盘自重，密度为7.8×103kg/m3，重力加速度为9.8 m/s2。

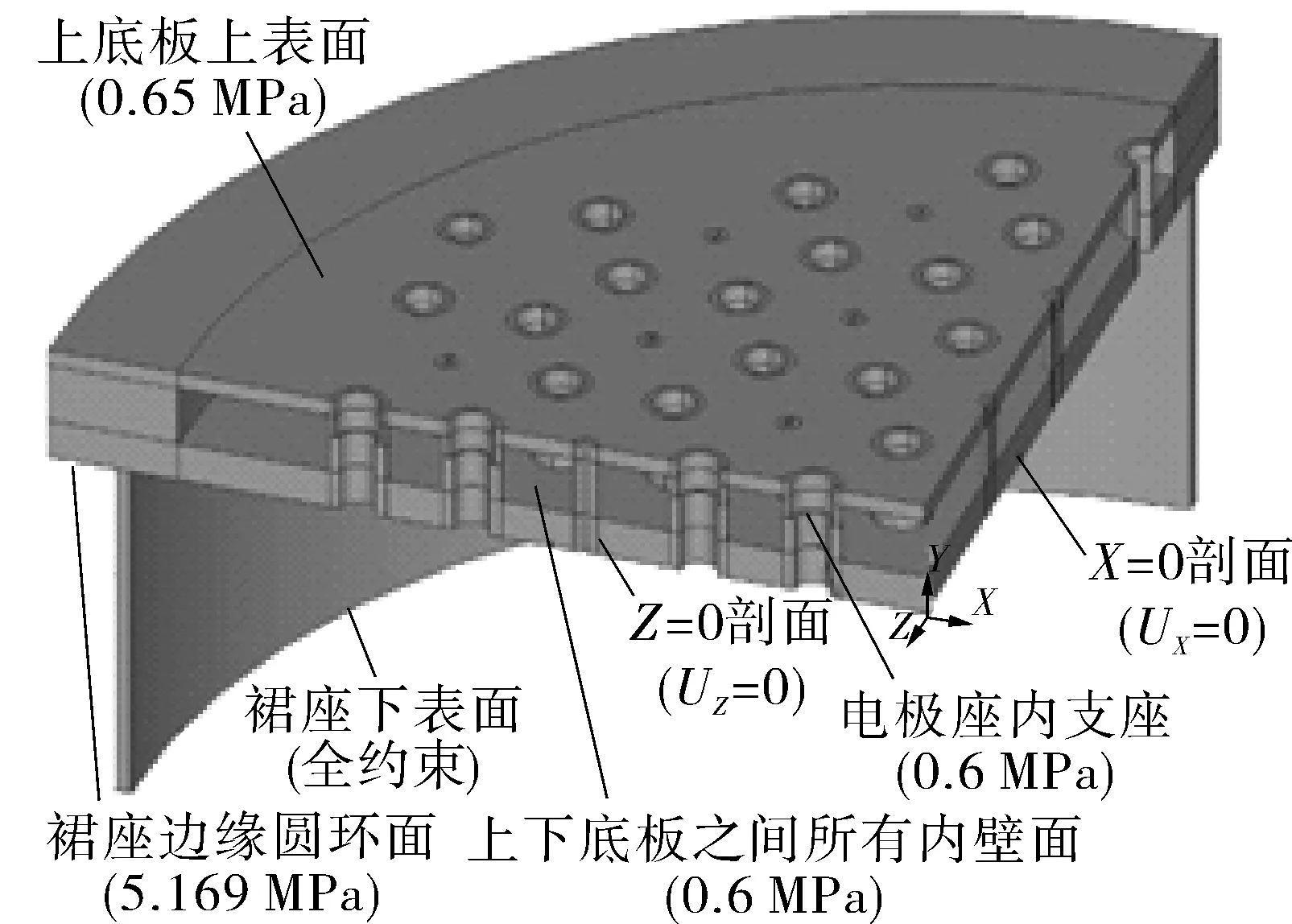
图3 应力分析边界条件示意

2 基于弹性应力分析法的应力强度评定

本部分的弹性应力评价按照JB 4732—1995进行。经过计算得到了该支撑结构的应力分布情况，图4示出了该结构各处的Tresca应力分布图，以及高应力区的局部放大图。可以看出，该结构中高应力区域位于电极座外表面与下底板相连接处，最大应力150 MPa。

2.1 电极座及进气口的应力分布情况

支撑结构的总体应力分布图和高应力区域A,B,C的应力云图如图4所示。可以看出，最大应力发生在电极座外表面与下底板相连接处，其最大应力为150 MPa。此外，电极座与上底板连接处内表面、电极座阶梯孔处内表面、进气口与上底板连接处内表面也存在高应力区。

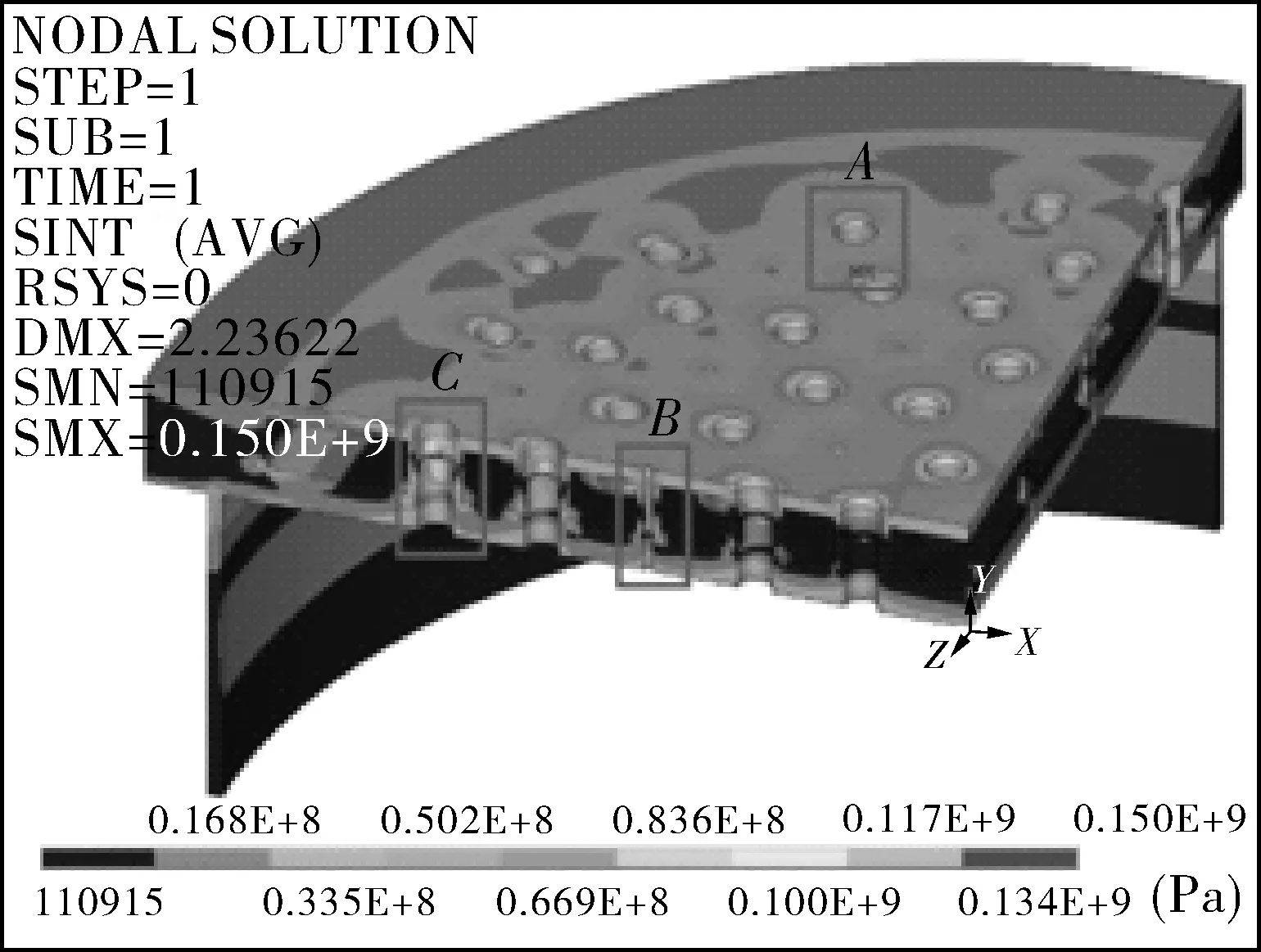
(a)总体示意图

(b)电极座(区域A剖面)

(c)进气口(区域B)

(d)电极座(区域C)

2.2 路径选择与应力评定

设置应力线性化路径，主要依据两条原则：(1)选择的线性化路径需沿壁厚方向距离最短，且需通过最大应力强度所在的点；(2)应力强度相对较高的区域，也需沿着壁厚方向设置线性化路径。基于上述原则，选择应力强度最大点所在的截面以及高应力区所在截面分别设定应力线性化路径(路径1～4)，如图4所示。

应力评定结果见表2。可以看出，所选路径的应力强度小于许用值，表明结构满足强度要求。需要说明，所评估路径仅存在一次局部薄膜应力和二次应力，不存在一次弯曲应力。

表2 应力线性化结果

3 基于极限载荷法的防止塑性垮塌评定

3.1 极限载荷分析法的基本假设

采用极限载荷法进行防止塑性垮塌评定时，需要对其进行假设：采用的材料模型为理想弹塑性；采用线性应变-位移的表达式；将平衡关系建立在未变形的结构上；采用的判断准则为von Mises屈服准则和关联流动法则。

3.2 载荷加载方式

本模型载荷施加过程中，涉及一次加载和比例加载，分别介绍如下。

(1)一次加载：主要是将载荷从0逐渐增大至最大值。值得注意的是，结构一旦进入塑性阶段，为保证求解收敛，应该不断减小所增加的载荷的增量。一旦增量过大，极易导致无法收敛的情况，从而造成极限载荷的误判。

(2)比例加载：由于该结构中存在着多种载荷，所有的载荷均按相同的百分比进行施加。其具体的载荷组合形式以及相应的载荷系数可根据ASME Ⅷ-2进行选取。

对于本文所研究的结构，考虑压力载荷和自重的共同作用，因此根据ASME Ⅷ-2中的总体准则，选择载荷系数为1.5，即利用ANSYS进行求解时，均按照实际工况载荷的1.5倍予以加载。

3.3 防止塑性垮塌评定

ASME Ⅷ-2中指出，造成整个结构失稳垮塌的载荷即是它的极限载荷[11]。而在具体的数值分析中，则体现为再增加一个极小的载荷也无法得到收敛解。由于材料模型为理想的弹塑性模型，因此，依据ASME Ⅷ-2选取材料的屈服强度为设计温度下许用应力的1.5倍，即σs=1.5Sm。

利用ANSYS对三维模型进行求解，最终得到收敛解，表明该模型满足强度要求。

3.4 载荷极限计算

求解该底盘结构的极限载荷，以计算强度裕量。经计算，其极限载荷为实际工况载荷的4.8倍，强度裕量较大。

4 基于弹塑性分析法的防止塑性垮塌评定

4.1 有限元模型

采用弹塑性分析法时，需满足如下要求：本构模型采用真实的应力-应变曲线；采用非线性的应变-位移表达式；根据已经变形的结构来建立平衡关系；采用von Mises屈服准则和关联流动法则。

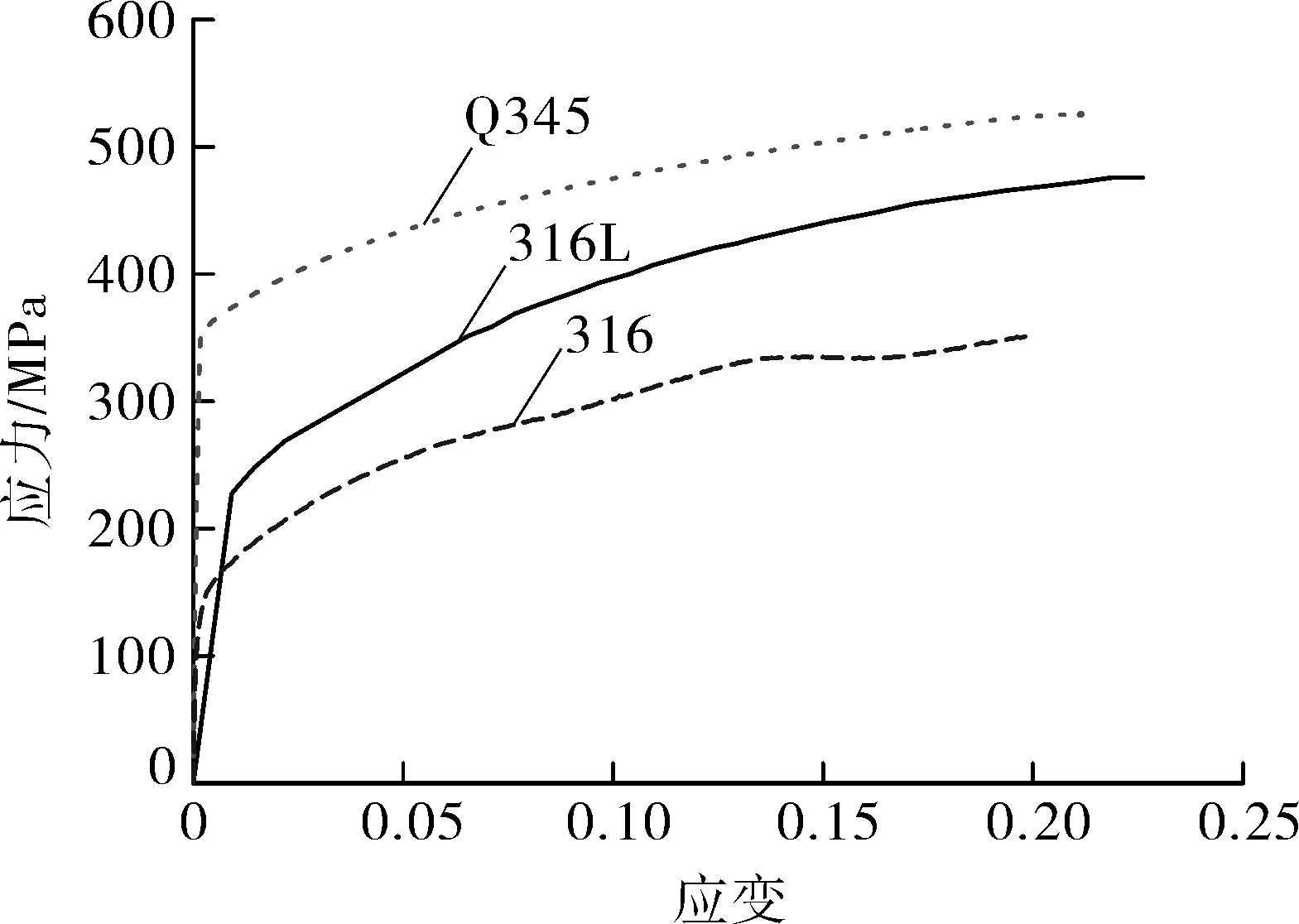
图5 材料真实应力-应变曲线

文中采用Q345，316L以及316材料的真实应力-应变曲线建立本构模型加以分析。需要说明，由于缺乏相应的材料数据，主体部位上底板、进气口、电极座的316L材料为300 ℃下的应力应变数据；下底板、法兰及裙座使用的Q345材料为常温下的应力应变数据；非主体部位出气口的316材料为650 ℃下的应力应变数据。上述材料的应力-应变曲线如图5所示。

4.2 边界条件

对于本文所研究的结构，考虑压力载荷和自重的共同作用，根据ASME Ⅷ-2中的总体准则，选择载荷系数为2.4，即均按照实际工况载荷的2.4倍加载。

4.3 防止塑性垮塌评定

对三维模型进行求解，最终得到收敛解，表明结构满足强度要求。

4.4 垮塌载荷计算

为了比较不同方法所得结果的强度裕量差异，计算了基于弹塑性材料模型的垮塌载荷。经计算，其垮塌载荷为实际工况载荷的8.8倍。

4.5 不同方法的比较

为比较3种方法的强度裕量，选取弹性应力分析法中许用极限与结构四类应力比值的最小值(经比较，为电极座与上底板连接处的许用极限与薄膜应力加弯曲应力的比值)、极限载荷法中极限载荷与工况载荷的比值以及弹塑性分析法中垮塌载荷与工况载荷的比值进行比较，具体数值如表3所示。结果表明，弹性应力分析法相对于其他两种方法结果更为保守；弹塑性分析法的强度裕量最大。