双分量玻色气体在有限温度下的力学稳定性和相分离
2019-08-22高佩佩贺丽余增强
高佩佩,贺丽,余增强*
(1.山西大学 理论物理研究所,山西 太原 030006;2.山西大学 物理电子工程学院,山西 太原 030006)
0 引言
量子多体系统的力学稳定性决定于粒子的统计属性和粒子间的相互作用形式。不同于费米子系统,玻色气体由于缺少量子简并压的支撑,因而其稳定性对相互作用格外敏感。在没有外势的情况下,理想玻色-爱因斯坦凝聚(BEC)具有无穷大的压缩率,热力学上仅处于稳定性的边缘。只有当气体原子间存在有效排斥相互作用时,BEC才真正达到稳定,成为可压缩的量子流体[1]。反之,当原子间存在吸引相互作用时,BEC会发生塌缩。实际上,这种失稳不仅出现在凝聚相,在正常相中塌缩也会发生[2]。
此前关于上述双分量玻色气体的理论研究大多局限于零温[3-7],关注的焦点集中在量子涨落对基态能量的贡献,而对热涨落效应的考察则很少涉及。本文将指出,有限温度时体系可以在高密度和低密度两个极限下保持稳定,而力学失稳出现在中等密度区间,这导致BEC相和正常相会以相分离的方式共存,由此我们给出了体系在有限温度的相图(如图1所示)。在接下来的篇幅中,我们将运用Hartree-Fock平均场理论具体阐释该相图是如何得到的,并指出发生相分离时体系的物态方程具有类似于经典气液相变的特征,最后我们讨论了在冷原子实验中如何观测这种相分离现象。
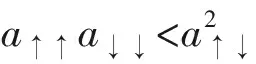
简单起见,以下设散射长度a↑↑=a↓↓=a,并限定a+a↑↓>0。在此参数条件下,Hartree-Fock理论给出的准粒子能谱总是正定的,且零温时没有自束缚态存在。后文的理论推导采用自然单位制,即令kB=ћ=1。数值计算中,我们取散射长度a=65a0(a0为玻尔半径),取玻色子质量m为39K原子的质量。
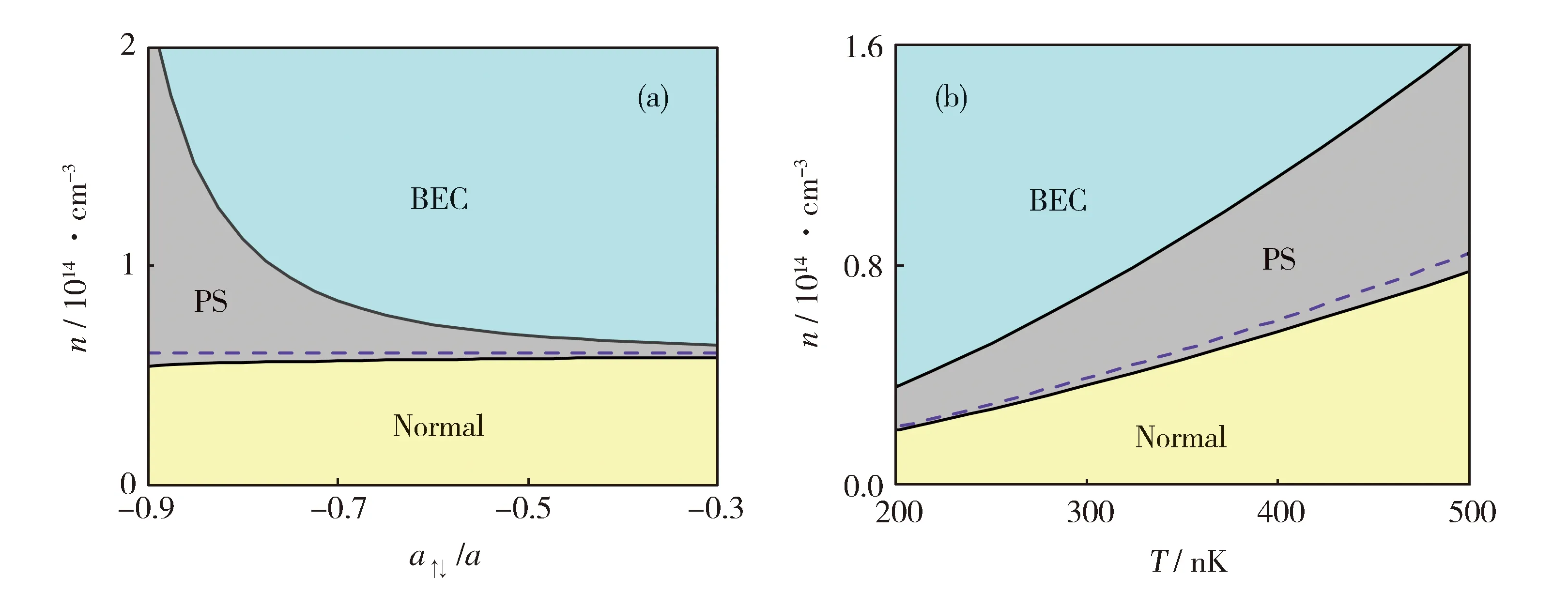
(a) Phase boundaries as functions of the inter-spin scattering length a↑↓ at temperature T=400nK.(b) Phase boundaries as functions of temperature for a↑↓=-0.8 a.PS represents the phase separation between BEC phase and normal phase.The dashed lines indicate the critical density for the BEC transition of an ideal gas.Fig.1 Phase diagram of a spin-half Bose gas with intra-spin repulsive interaction and inter-spin attractive interaction(a)温度T=400 nK时,相边界随散射长度a↑↓的变化。(b)散射长度a↑↓=-0.8 a时,相边界随温度的变化。 PS表示BEC相与正常相之间的相分离,虚线为理想气体BEC相变的临界密度图1 具有同自旋排斥相互作用、反自旋吸引相互作用的双分量玻色气体的相图
1 均匀体系的相变与力学稳定性
1.1 铁磁相变与BEC相变
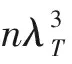
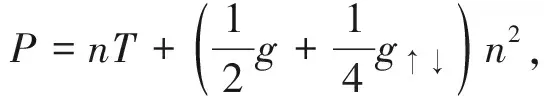
(1)
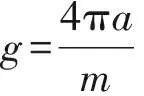

(2)
在弱相互作用情形下,凝聚体满足如下物态方程
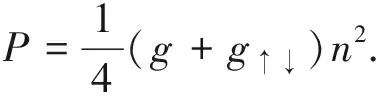
(3)
值得注意的是,凝聚波函数(2)是自旋算符σx的本征态,也就是说,BEC是自旋横向极化的铁磁态。
当原子密度n由小到大连续变化时,物态方程会从(1)式逐渐过渡到(3)式,相应地,体系的平衡态会从无凝聚、无自旋极化的正常相演化到自旋横向极化的BEC相。在此过程中,会先后经历铁磁相变和BEC相变。可以在平均场理论的框架下通过引入序参量描述这两次相变过程。
我们在Hartree-Fock近似下写出体系的巨正则哈密顿量

(4)
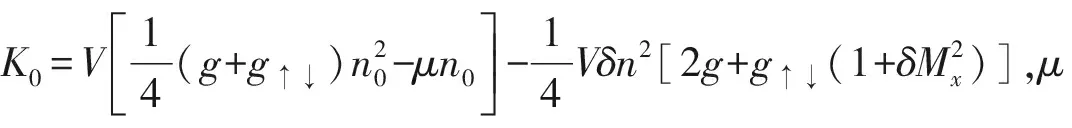
平均场哈密顿量(4) 可以在准粒子表象下写为对角化的形式

(5)

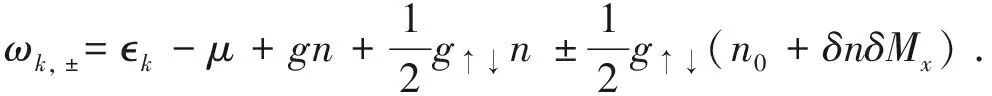
(6)
平均场参量δn和δnδMx可以通过下面的自洽方程求解

(7)
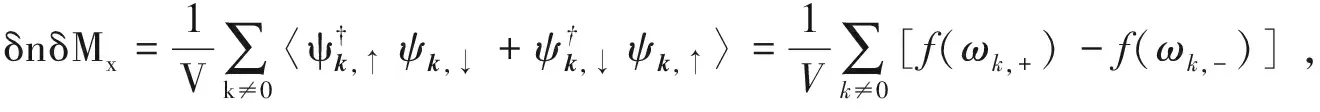
(8)
这里〈…〉表示算符的热力学平均,f(ω)=1/(eω/T-1)为玻色分布函数。
我们先来讨论没有玻色凝聚的情况(即n0=0,δn=n)。
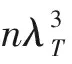

(9)
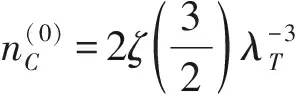
下面再来考虑出现玻色凝聚的情况(即n0>0)。
在BEC相中,凝聚密度的取值应满足极值条件〈∂K/∂n0〉=0,该条件又可进一步明确写为
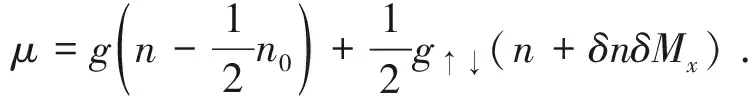
(10)
在BEC相变的临界点nC处,凝聚密度为零。将n0=0代入上式,并联立自洽方程(7)、(8),即可求得nC。在弱相互作用条件下,铁磁相变与BEC相变的临界点非常接近,nC仅比nM略大。解析上可以证明,二者之差的头阶项正比于a↑↓的平方。
以上分析表明,当原子密度由小到大连续变化时,铁磁相变会先于BEC相变出现。当n
需要说明的是,铁磁相变和BEC相变既可以通过固定温度、变化密度来实现,也可以通过固定密度、变化温度来实现。我们的考察采用了前一种方式,这种处理在后文求解等温压缩率时会更加方便。
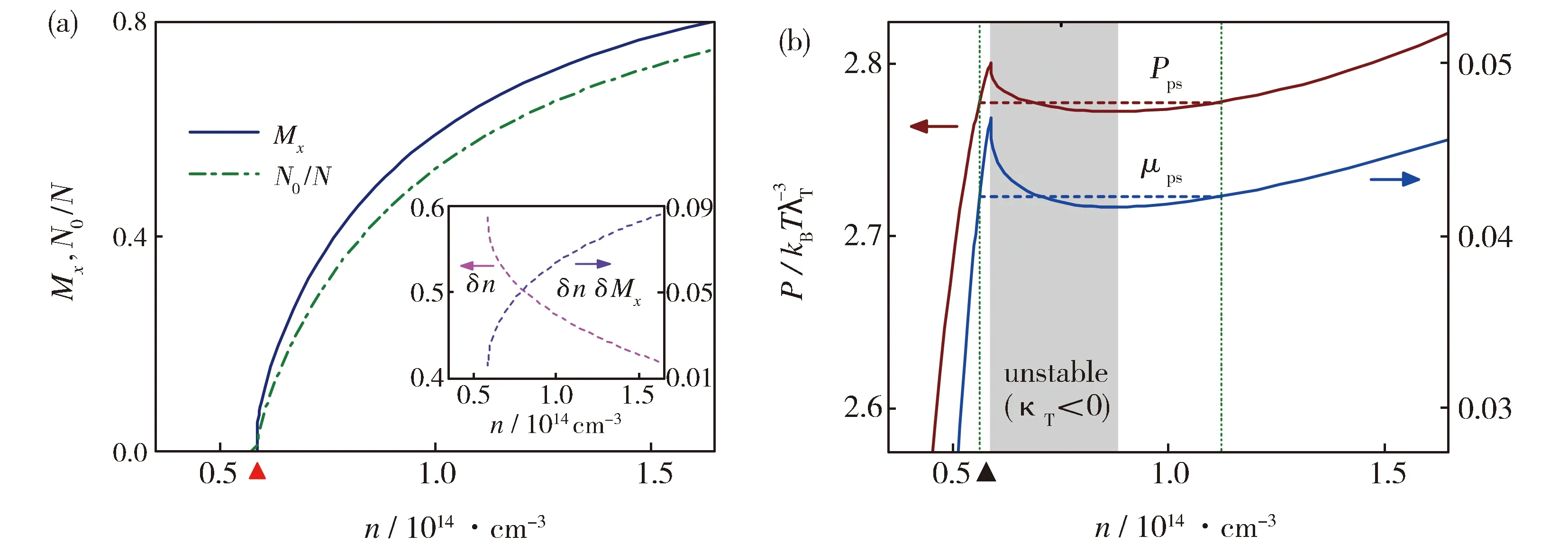
(a)Inset: density and magnetization density of thermal atoms as functions of n in the BEC phase.(b) In the shadow region, the system is unstable due to the negative compressibility.The vertical dotted lines indicate the densities satisfying the equilibrium conditions when the phase separation takes places. In both plots, the symbol ▲ marks the magnetic phase transition point nM, which is close to the critical point of BEC transition nC. For the displayed scale, the two critical points almost coincide. Parameters: temperature T=400 nK, and inter-spin scattering length a↑↓=-0.8 aFig.2 (a) Transverse magnetization Mx and condensate fraction N0/N as functions of density n at a constant tempe rature in the homogenous case;(b) Isothermal P-n and μn curves for the homogenous system.(a)插图为BEC相中热原子的密度δn与磁化密度δnδMx随n的变化曲线。(b)在阴影区域中体系的压缩率κT为负值, 因而是不稳定的。竖直点线的位置对应于发生相分离时满足平衡条件的密度值。两图中用符号▲标记磁化相变的临界点nM,BEC相变的临界点nC与其非常接近, 在图示尺度下二者几乎完全重合。选用参数:温度T=400 nK,散射长度a↑↓=-0.8 a图2 (a)给定温度下,均匀体系的横向磁化强度Mx与凝聚分数N0/N随密度n的变化曲线;(b)均匀体系的等温P-n曲线和μ-n曲线
1.2 力学稳定性
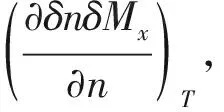
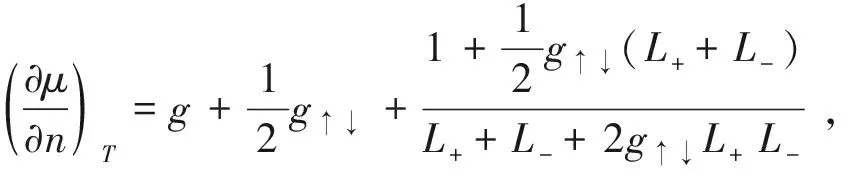
(11)
其中
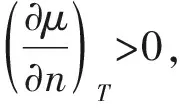
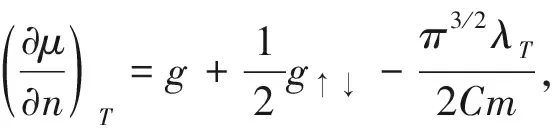
(12)
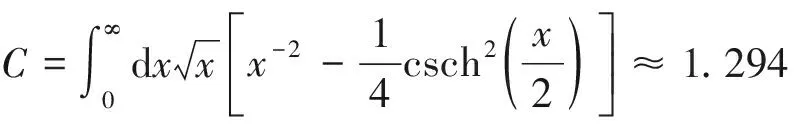
现在来讨论玻色凝聚相(即n0>0)。BEC相的凝聚密度n0满足极值方程(10)。在固定温度下,对该方程两边求n的偏导,可得
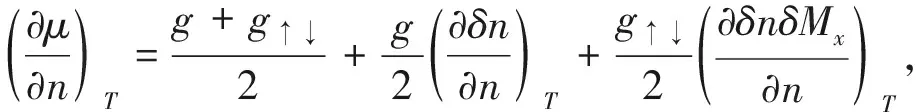
(13)
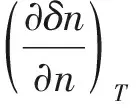
以上分析可以通过图2(b)中的等温P-n曲线和μ-n曲线更直观地体现出来。在高密度或低密度极限下,P和μ均随n单调增加,因此体系是稳定的。而在中间一段密度范围内(以nM为起点、一直延伸到BEC相的一部分),P和μ是n的减函数,表明均匀体系在此区间内会发生力学失稳。
2 相分离与物态方程
在等温压缩率小于零的区间内,均匀体系会发生旋节分解(spinodal decomposition)[13]:其中一部分原子自发地相互聚集,形成高密度的稳定相,其余原子则变得更加稀薄,形成低密度的稳定相。这种过程最终会达到动态平衡,从而导致高密度相与低密度相的相分离。两相平衡的热力学条件为
P(n1)=P(n2)=PPS,
(14)
μ(n1)=μ(n2)=μPS,
(15)
其中n1、n2分别为共存态下两相的密度,PPS和μPS为相平衡的压强和化学势。对于我们考虑的双分量体系,低密度相为无玻色凝聚、无自旋极化的正常相,高密度相为自旋横向极化的BEC相。
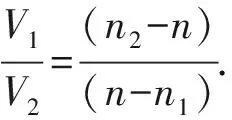
在考虑了相分离因素之后,我们可以写出体系完整的物态方程。对于均匀相(n
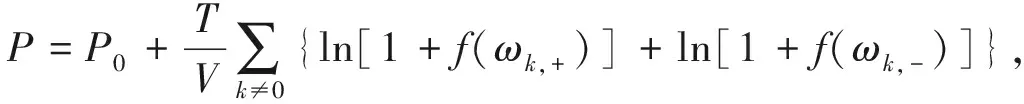
(16)
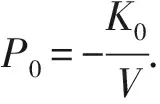

综合以上关于相分离和物态方程的分析,最终我们得到了如图1所示的有限温度相图,其中相分离区间的大小依赖于相互作用强度和温度。在适当的参数条件下,该区间可以覆盖相当大的实验可观测的密度范围。
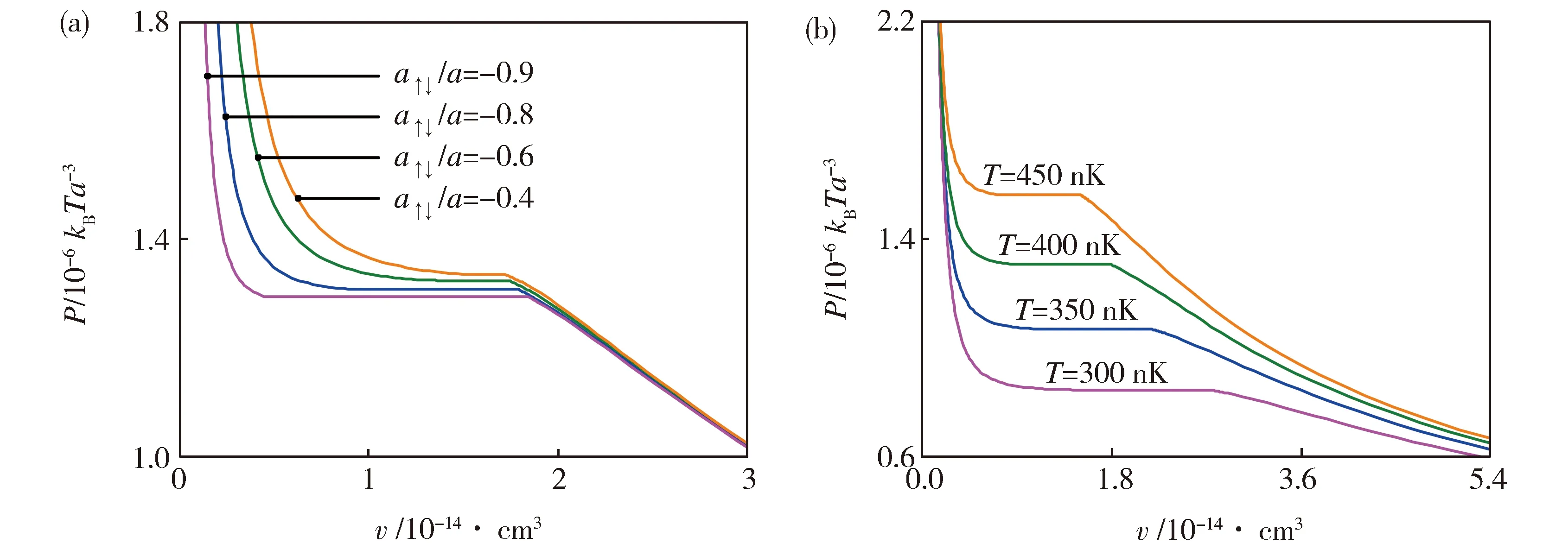
Fig.3 Isothermal P-v curves for various scattering lengths and temperatures. The horizonal segments correspond to the coexistence states of BEC phase and normal phase In (a),temperature is fixed at T=400 nK; In (b), inter-spin scattering length is fixed at a↑↓=-0.8 a图3 散射长度和温度取不同值时的等温P-v曲线,其中的水平线段对应于BEC相与正常相的共存态(a)中取固定的温度T=400 nK; (b)中取固定的散射长度a↑↓=-0.8 a
3 简谐势阱中的密度分布
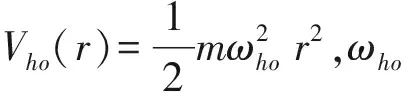
当发生相分离时,为了降低体系的势能,原子云会自发地成形成壳层结构:高密度的BEC相会集中在势阱的中心区域,低密度的正常相则分布势阱的外围。由于BEC相与正常相之间存在密度差,这就导致在核心区域与外壳层之间的相边界处会出现密度跳变。实验上,可以利用原位成像技术直接观测原子云的密度分布,进而通过密度分布的不连续性确认相分离的发生。
对于典型的实验参数,外势场随空间的变化尺度aho=(mωho)-1/2远大于凝聚体的相干长度以及原子的热波长,因此可以在半经典图像下采用局域密度近似计算原子的密度分布[14]。在该近似下,r点处的密度被写为局域化学势μ(r) 的泛函,在空间中的每一点,n(r) 和μ(r) 满足无外势时求得的物态方程。μ(r) 由下式关系给出
μ(r)=μ0-Vho(r) ,
(17)
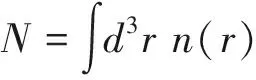
图4中画出了根据局域密度近似计算得到的简谐势阱中的原子密度分布。可以看到,在相边界处(竖线所在位置)原子的总密度和凝聚密度都发生了跳变,n(r)的跳变幅度即对应于相图中相分离区间的大小。在BEC临界温度以下,温度越高,密度跳变的幅度越大;而在较低的温度,密度跳变则很不明显。这意味着,实验上为了更明确地观测相分离现象须把温度控制在一个合理的范围之内。

The vertical dotted lines indicate the boundary between BEC phase and normal phase, where the density profiles exhibit a sudden jump. Parameters: total number of atoms N=5×105, trapping frequency ωho=2π×150 Hz, inter-spin scattering length a↑↓=-0.8 a, temperature T=400 nK in (a) and T=340 nK in (b)Fig.4 Density distribution functions of atomic density and condensate density in a harmonic trap竖直点线位置为BEC相与正常相的相边界,在该边界上密度分布出现跳变。 原子总数N=5×105,势阱频率ω=2π×150 Hz,散射长度a↑↓=-0.8 a。(a)和(b)图中温度分别为400 nK和340 nK图4 简谐势阱中原子密度及凝聚密度的径向分布
4 讨论与结论

本文考察了双分量玻色气体在有限温度的力学稳定性,并预言了正常相与BEC相之间的相分离。在两相共存区间,体系的物态方程呈现出类似经典气液相变的特征,这为探索量子液滴态的形成机制提供了新的线索。在简谐势阱中,相分离会导致原子云密度在相边界处发生跳变,通过数值模拟,我们讨论了利于实验观测的温度范围。
