采煤机截割减速器典型故障特征
2019-08-22张亮
张亮
(西山煤电集团公司 屯兰煤矿,山西 太原 030200)
0 引言
近年来随着工业技术的不断发展,煤矿产业也得到发展,研究资料表明,未来几年煤炭仍然是我国的主要能源资源,占比将达到70%左右[1-3]。采煤机作为煤矿开采中的主要大型设备,其性能及可靠性对企业高效高产的目标具有重要影响。生产过程中,由于采煤机工作环境恶劣,需要承受煤体和岩石的巨大冲击载荷,同时设备功率不断增大,新技术的不断升级和应用,电气控制系统越来越复杂,使得采煤机故障判断和排除比较困难,采煤机传动部分经常发生故障,据已有资料统计,约有80%的故障是由齿轮问题引起的,可见齿轮失效是采煤机故障的主要诱因之一[4],因此有必要对采煤机齿轮及齿轮箱的故障进行分析研究。
本文以采煤机齿轮箱为研究对象,对其常见故障及其故障特征进行提取,以减少生产过程中齿轮箱故障的判断和排除时间,提高生产效率。
1 采煤机截割减速机工作原理
图1为采煤机截割减速器传动示意图,从图中可以看出,截割部中间减速器通过输入轴将扭矩传递给减速器,经减速后通过行星架传递给两侧滚筒,进而进行割煤工作。其中锥齿轮对作为输入与输出的主要转换部分,对减速电机的性能具有重要影响。

图1 采煤机截割减速器传动示意图
2 齿轮系统振动机理分析
2.1 齿轮系统的简化模型
采煤机齿轮箱及齿轮振动系统是一个多变量复杂的系统,具有非线性、高耦合、高阶的特点,要建立完整的齿轮箱非线性模型比较困难,故在分析过程中有必要对模型进行简化。根据齿轮啮合原理,通常简化方法是将一对齿轮啮合过程简化为一个振动系统,其中包含质量、阻尼和弹簧,简化模型如图2所示[5]。

图2 齿轮啮合振动模型
其动力学方程为:
Mx+Cx+K(t)x=F(t)
(1)
式中:F(t)为齿轮系统所受的外载荷;M为齿轮副的等效质量,M=m1·m2/(m1+m2);C为齿轮对啮合处阻尼;x为不同啮合齿对在啮合线上的相对位移,若齿轮1的位移为x1、齿轮2的位移为x2,则x=x2-x1;K(t)为齿轮对啮合处刚度。
通常情况下,将齿轮系统所受的外部激励表达为:
F(t)=K(t)E1+K(t)E2(t)
(2)
式中:E1为齿轮受到平均静弹性变形,不受齿轮啮合误差和故障的影响,K(t)E1主要反映齿轮的常规啮合振动;E2(t)为齿轮的故障函数,主要受齿轮啮合误差及齿轮故障的影响。
一对齿轮在正常啮合过程中,工作齿数是呈规律变化的,由一对齿啮合到两对齿同时啮合,再到一对齿啮合,交替变化过程中齿轮受到周期性冲击载荷,形成齿轮的啮合振动,啮合频率和谐频可表达为:
(3)
式中:fz为齿轮的啮合频率;N为自然数;M、m为最大谐波次数;n为齿轮工作转速,r/min;Z齿轮齿数。
2.2 齿轮的啮合刚度
齿轮在啮合过程中,啮合刚度是一个重要参数,由于齿轮啮合过程中出现一对齿、两对齿交替啮合的情况,分析可知,在承载不变的情况下,单对齿啮合时的弹性变形比两对齿啮合时大,两对齿啮合时啮合刚度更大。齿轮的啮合特性使得啮合刚度发生突变,如图3所示,图3(a)直齿啮合过程啮合刚度突变较大,图3(b)斜齿和人字齿啮合刚度变化平缓。

(a)(b)图3 齿轮啮合刚度变化曲线
由于齿轮啮合过程中啮合齿数的周期变化,使得齿轮的啮合刚度K(t)随着变化,最终啮合频率和高次谐波成分同时在齿轮振动信号中出现。啮合频率及谐频可表达为:

(4)
式中:n1为主动轮转速;n2为从动轮转速;z1为主动轮齿数;z2为从动轮齿数。
由上可知,齿轮在正常运行和故障状态下,振动信号中始终存在啮合频率和谐波成分,可以根据振动差异性来辨别齿轮工作状态情况。
3 采煤机截割减速机故障仿真
3.1 锥齿轮对动力学模型建立
使用Pro/Engineer软件完成配对锥齿轮的实体建模和装配[6],如图4所示。将三维模型导入ADAMS软件中进行动力学分析,具体参数为:小锥齿齿数Z1=20,大锥齿齿数Z1=30,平均模数均为m=10,泊松比λ=0.29,杨氏模量E=2.07×105N/mm,锥齿轮间的接触刚度系数为K=11.67×105N/mm1/2,设定输入轴转速为180 r/min,负载扭矩为2.5×107N·mm。通过添加相应的约束、载荷、驱动和接触力,对上述模型进行动力学仿真分析。

图4 锥齿轮对装配示意图
3.2 仿真分析结果
仿真过程中,分别对断齿故障和齿型误差故障两种不同状态下的大锥齿轮进行模拟仿真,图5所示为人为设置的断齿故障示意图。在设置齿型误差时,将大锥齿轮的轮廓曲线单边往里偏移0.2 mm,分别对上述两种故障进行动力学仿真,并对仿真数据进行提取。

图5 断齿齿轮示意图
为了从两种故障的仿真数据中提取故障特征,将仿真数据通过Import Data导入到MATLAB软件中,再对故障信号分别进行时域和频域分析,其中频域分析中增加了解调谱分析。
图6~8所示为大锥齿轮断齿故障发生后的时域和频域分析结果。从图6看出,断齿故障发生后,断齿对齿轮啮合力产生周期冲击力,该冲击力的频率与齿轮理论转频接近,约为2.01 Hz。从图7看出,断齿故障后齿轮在频率59.9 Hz、120 Hz、180 Hz处啮合力出现峰值,这些频率与齿轮啮合固有频率60 Hz及高次谐波接近,且边频较宽,幅值较高。图8所示的锥齿轮对啮合力解调谱中,在1.831 Hz、8.057 Hz、17.94 Hz等处啮合力出现峰值,与故障齿轮的理论转频和多次高阶谐波接近。
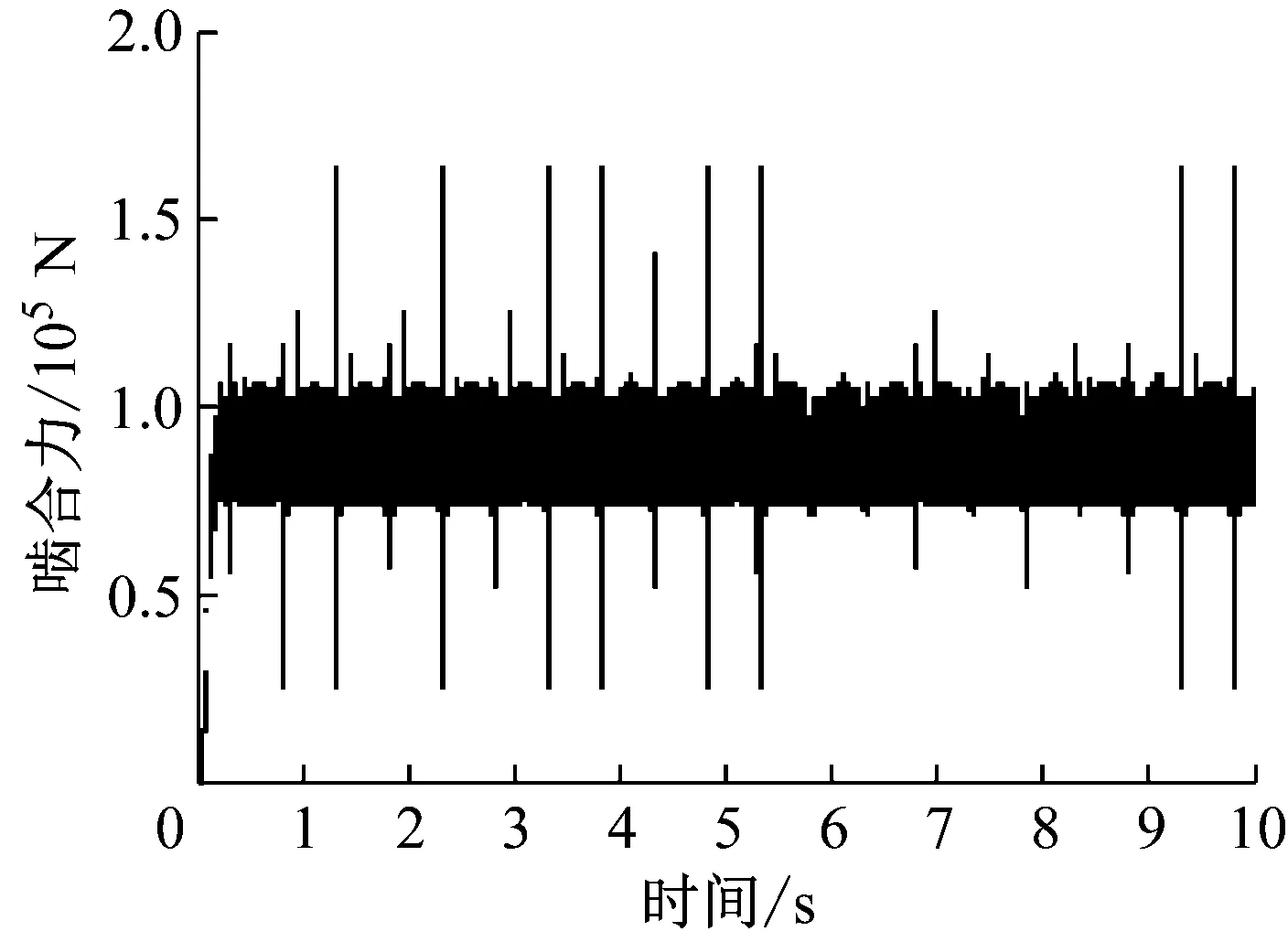
图6 锥齿轮对啮合力时域分析

图7 锥齿轮对啮合力频域分析

图8 锥齿轮对啮合力解调谱分析
图9~11所示为大锥齿轮发生严重齿型误差故障时时域和频域分析结果。

图9 锥齿轮对啮合力时域分析
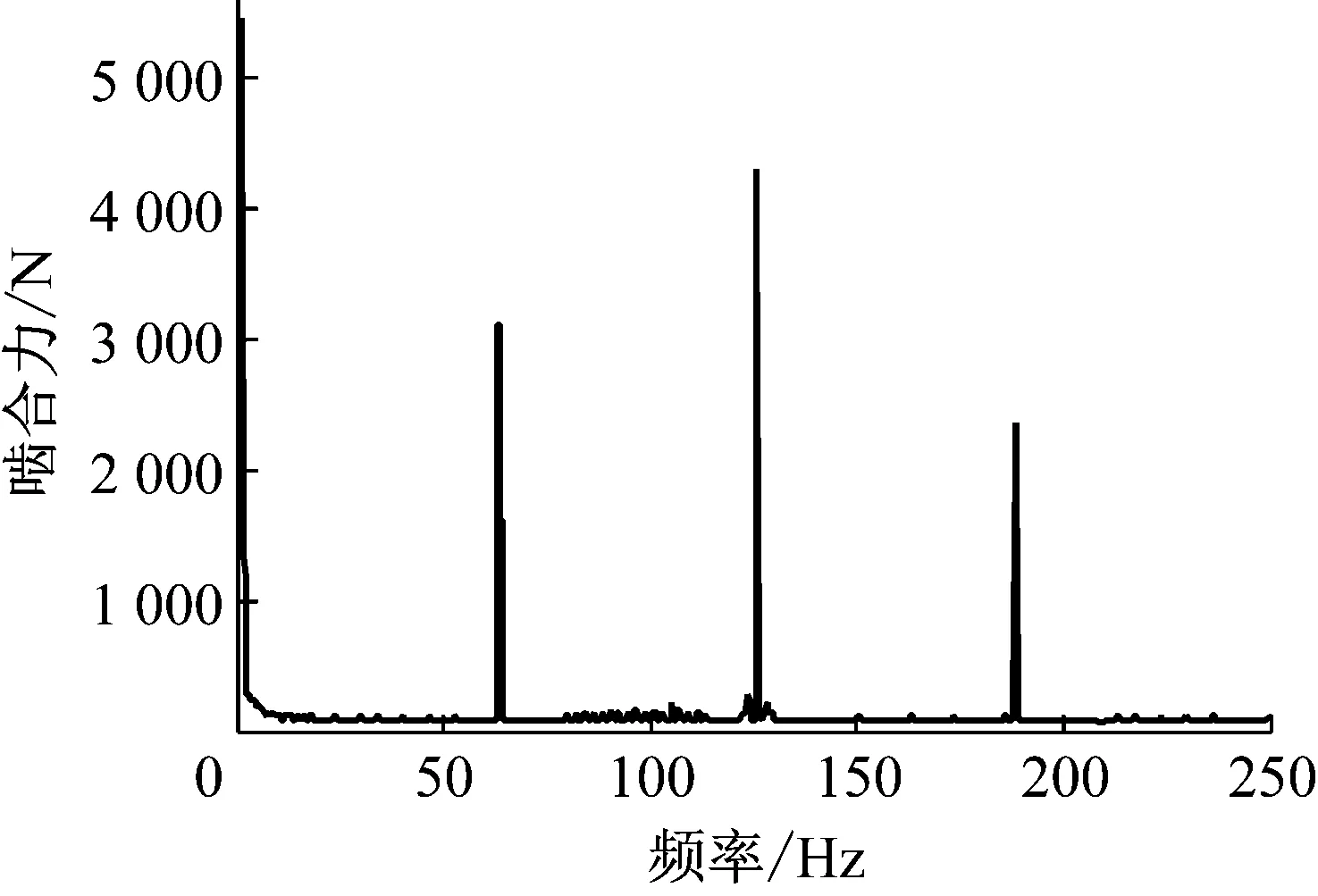
图10 锥齿轮对啮合力频域分析

图11 锥齿轮对啮合力解调谱分析
从图9看出,在该故障发生后,齿轮啮合力产生周期性冲击力,并且该冲击力的频率2.02 Hz与齿轮理论转频接近,但是冲击力的幅值要远小于断齿故障时冲击力幅值。从图10看出,故障后齿轮在频率60 Hz、120 Hz、180 Hz处啮合力出现峰值,这些频率与齿轮啮合固有频率60 Hz及高次谐波接近,且边频较窄,幅值较小。图11所示的锥齿轮对啮合力解调谱中,在1.83 Hz处啮合力出现峰值,与故障齿轮的理论转频接近,且齿型误差解调谱主要以齿轮的一级转频为主。
4 结论
通过建立采煤机截割减速器中锥齿轮对啮合的三维模型,应用ADAMS软件对其进行了动力学分析。仿真过程中主要以齿轮对啮合过程中齿型误差和断齿两种常见故障为分析目标。分析结果表明,锥齿轮对发生断齿和齿型误差时,时域图均出现了较明显的周期性冲击力,该冲击力的频率与齿轮理论转频接近,但齿型误差故障时,冲击力的幅值要远小于断齿故障时冲击力幅值。频域分析中,两种故障均在齿轮啮合固有频率60 Hz和高次谐波附近出现啮合力最大值,但断齿时边频较宽,幅值较高,齿型误差故障时边频较窄,幅值较小。解调谱分析中,断齿时啮合力发生频率与故障齿轮的理论转频和多次高阶谐波接近,齿型误差解调谱主要以齿轮的一级转频为主。由此,两种典型故障具有明显的特征曲线,根据分析结果可以判定齿轮对故障类型,可为减速器故障诊断提供依据。
