采煤机截割部双列圆锥滚子轴承 疲劳寿命与轴向游隙的关系
2019-08-22阚锦彪
阚锦彪
(天地科技股份有限公司 上海分公司, 上海 200030)
0 引言
轴承游隙的大小对双列圆锥滚子轴承的接触载荷分布有直接影响,而载荷分布的不同也会影响轴承的疲劳寿命。通过查阅文献发现,双列圆锥滚子轴承疲劳寿命的研究对象多为风力发电设备、高铁或汽车,对于大功率采煤机截割部中双列圆锥滚子轴承的疲劳寿命的研究未见有相关文献[1-6]。本文将对大功率采煤机截割部中双列圆锥滚子轴承的疲劳寿命随轴向游隙的变化关系进行研究,为轴承游隙的选择提供参考依据。
1 接触载荷分布分析
在经典的轴承分析理论中,采用了轴承内、外圈为刚性套圈的假设,即在载荷作用下轴承的位移只表现为内、外圈之间的刚体移动,套圈与滚动体之间的接触也只具有局部性质,而对套圈的整体形状不会产生影响。这一假设大大简化了分析计算,其分析结果完全可以接受,为此,以下的分析沿用这个假设[7]。
如图1所示,双列圆锥滚子轴承在外界力和力矩的作用下,内、外圈会产生相对线位移和角位移。分析时可将两个内圈和中间的隔圈视为一个整体,以轴承中心为原点定义一个坐标系,当轴承承受沿3个坐标轴方向的分力Fx、Fy和Fz,以及yz平面内的分力矩Myz和xz平面内的分力矩Mxz时,轴承内圈相对于外圈会产生沿3个坐标轴方向的线位移δx、δy和δz,以及yz平面内的角位移θyz和xz平面内的角位移δxz。

图1 内外圈相对位移
图2中在内外圈发生径向位移δr时,由于是刚体运动,则在i个滚子处产生的径向位移应为δri:
δri=δrcosφi
(1)

图2 径向位移
图3中在内外圈发生角位移θ时,则在i个滚子处的产生角位移应为θi:
θi=θcosφi
(2)

图3 角位移
当内外圈同时发生线位移δx、δy和δz,以及yz平面内的角位移θyz和xz平面内的角位移δxz时,则第i个滚子处总的的径向位移δrti和轴向位移δati应为:
第一列:
(3)
第二列:
(4)
其中,R1为滚子中心到轴承中心的距离在径向上的投影,R2为滚子中心到轴承中心的距离在轴向上的投影,如图4所示。

图4 滚子中心与轴承中心距离的投影
图5中在第i个滚子处法线方向总位移δnti应为:
δnti=δrticosαe+δatisinαe
(5)
式中:αe为圆锥滚子与外圈的接触角。
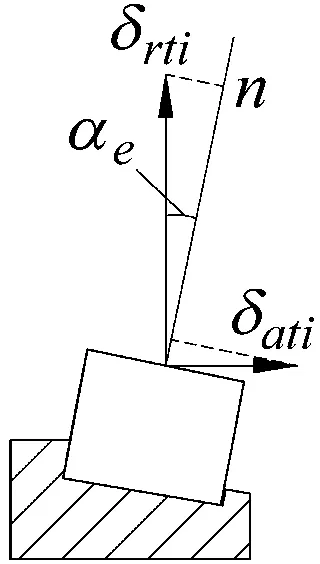
图5 法线方向总位移
假设双列圆锥滚子轴承的轴向游隙为ua,则第i个滚子处法线方向变形量δni为:
δni=δnti-uasinαe
(6)
根据Palmgren公式,第i个滚子与外圈的接触载荷Qei为:
(7)
式中:Kne为滚子与外圈的接触刚度系数。
Qei在x、y、z轴方向上分量Qxi、Qyi和Qzi分别为:
Qxi=Qeicosαesinφi
(8)
Qyi=Qeicosαecosφi
(9)
Qzi=Qeisinαe
(10)
在yz平面内,由接触载荷Qei产生的抵抗力矩Meyz应为:
(11)
在xz平面内,由接触载荷Qei产生的抵抗力矩Mexz应为:
(12)
将两列轴承的相应载荷叠加,可得到双列圆锥滚子轴承的平衡方程为:
(13)
式中:i为每列滚子的个数;j为轴承列数。
此式(13)就是以内圈相对于外圈沿着3个坐标轴方向的线位移δx、δy和δz以及yz平面内的角位移θyz和xz平面内的角位移θxz为未知量的非线性方程组,可以采用Newton-Raphson迭代法求解,得到δx、δy、δz、θyz和δxz的数值之后,便可进一步求得双列圆锥滚子轴承每个滚子与外滚道之间的接触载荷Qei。
由于大功率采煤机选用的双列圆锥滚子轴承的滚子圆锥角比较小,故内外圈接触载荷可认为是相等的,而挡边接触载荷可忽略不计。由此,通过改变轴向游隙的数值,可进一步求解得到内外圈接触载荷分布随轴向游隙的变化数据。
2 疲劳寿命分析
双列圆锥滚子轴承属于线接触的轴承,故在采煤机工作时,轴承内圈转动,而外圈静止。根据T.A.Harris的分析[8-9]:
1) 线接触轴承滚子与内滚道接触的疲劳寿命可按下式计算:
(14)
式中:Li为滚子与内滚道接触的疲劳寿命,106r;Qci为滚子与内滚道的额定接触载荷,N;Qi为滚子与内滚道的当量接触载荷,N。
2) 滚子与内滚道的额定接触载荷Qci按下式计算:
(15)

3) 滚子与旋转的内滚道的当量接触载荷按下式计算:
(16)
式中:Qi为滚子与内滚道的当量接触载荷,N;Qj为每个滚子与内滚道接触载荷,N;Z为每列滚动体个数。
4) 滚子与外滚道接触的疲劳寿命按下式计算:
(17)
式中:Le为滚子与外滚道接触的疲劳寿命,106r;Qce为滚子与外滚道的额定接触载荷,N;Qe为滚子与外滚道的当量接触载荷,N。
5) 滚子与外滚道的额定接触载荷Qce按下式计算:
(18)
6) 滚子与静止的外滚道的当量接触载荷按下式计算:
(19)
式中:Qe为滚子与外滚道的当量接触载荷,N;Qk为每个滚子与外滚道接触载荷,N;Z为每列滚动体个数。
7) 双列圆锥滚子轴承的整体疲劳寿命按下式计算:
(20)
式中:L为双列圆锥滚子轴承整体疲劳寿命,106r;Li为滚子与内滚道接触的疲劳寿命,106r;Le为滚子与外滚道接触的疲劳寿命,106r。
根据接触载荷分布分析得到的双列圆锥滚子轴承滚子与内外圈之间的接触载荷随轴向游隙变化的数据,通过疲劳寿命计算公式可得到双列圆锥滚子轴承的疲劳寿命随轴向游隙的变化数据,绘制成曲线图,如图6所示。
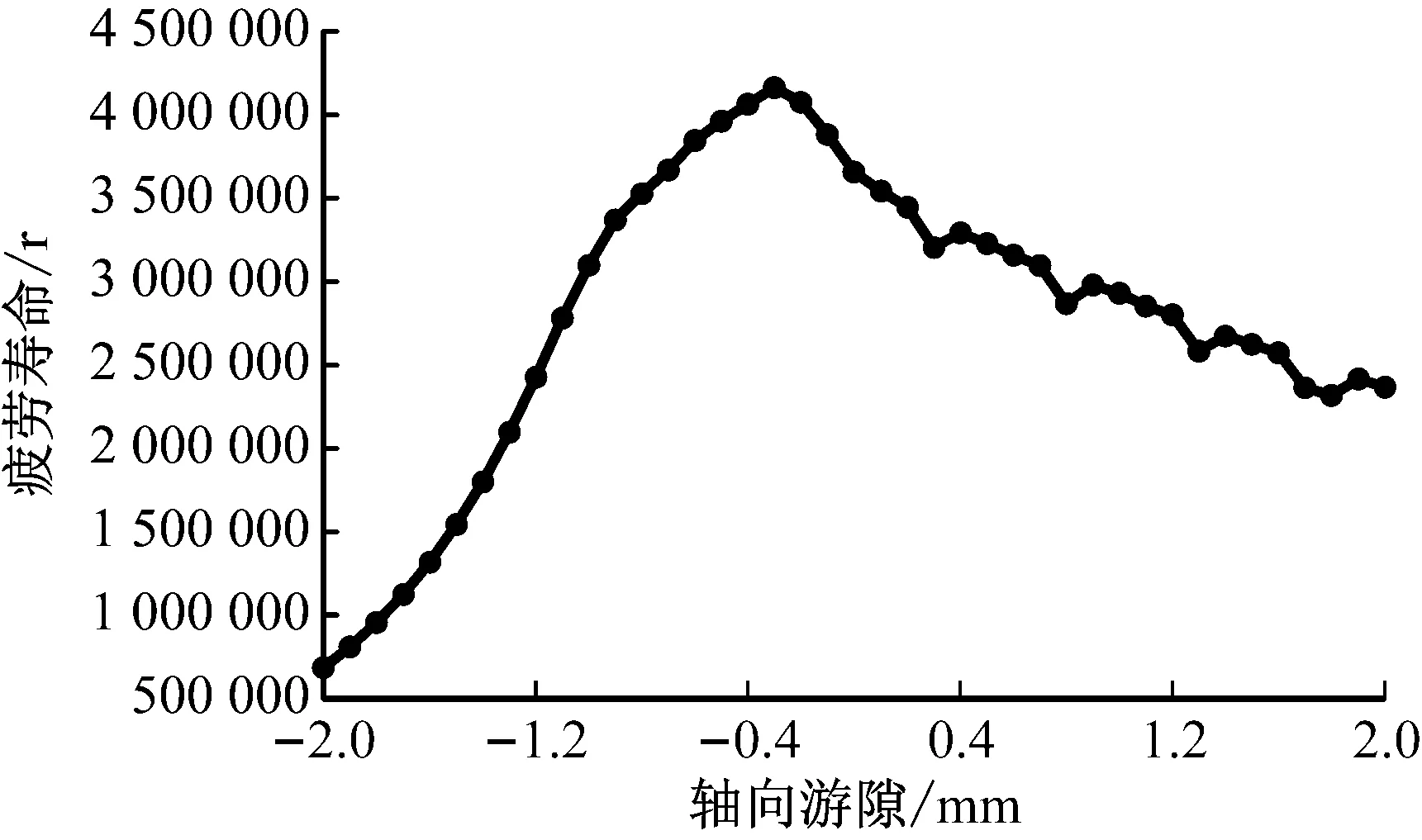
图6 疲劳寿命随轴向游隙的变化规律
由图6可以看出,当轴向游隙为-0.3 mm时,双列圆锥滚子轴承的疲劳寿命最大;当轴向游隙由-0.3 mm往负游隙方向变化时,疲劳寿命的下降斜率比较大,而当轴向游隙由-0.3 mm往正游隙方向变化时,其疲劳寿命的下降斜率趋于平缓。
3 结论
通过理论计算分析,得到大功率采煤机截割部中双列圆锥滚子轴承滚子与内外圈之间的接触载荷随轴向游隙变化的数据,通过疲劳寿命公式计算,得到轴承疲劳寿命随轴向游隙的变化数据,并绘制成曲线图,总结了双列圆锥滚子轴承的疲劳寿命与轴向游隙的变化关系,为轴承游隙的选择提供了参考依据。
