基于Freefem++的有限元数值计算在计算物理中的应用

(贵州师范大学物理与电子科学学院，贵州 贵阳550001)

计算物理以物理知识和数学方法的综合应用为主，在理工科类专业具有重要意义，特别是以科学研究为主要培养方向的物理学专业[1]。这门课程的典型特征是数值计算，涉及较多偏微分方程的数值求解，对众多学生而言相对困难[2-3]。在众多数值方法中，除了有限差分方法外，有限元方法也得到了广泛的应用，在科学研究和工程实践中具有重要意义。有限差分方法以快速计算为特征，精度一般不如有限元，特别是处理格网边界时，这种弊端非常显著。有限元方法基于分片插值函数，边界更接近于真实情况，误差相对较小。这样的优点在实际应用中至关重要，特别是工程技术中。近十年来，随着计算机技术的发展，有限元并行计算的应用使得费时问题得到了解决，有限元技术在工程应用中得到了快速的发展和普及。在计算物理领域，除了上述数值方法外，具有更多优点的边界元和有限体积方法也得到了快速的发展[4-7]。当前市场上主流数值计算软件，以有限元为主，因此，有限元在科研和工程技术中的应用至关重要。

作为综合性高校，培养数值计算方向的学生至关重要，特别是培养有限元专业知识技能的学生更是未来教育发展方向和市场所需。目前主流有限元软件众多，如Ansys、MSC、Abaqus、COMSOL等，这些商业闭源软件在业界具有良好的口碑，可靠性较好。但这些软件由于相关模块被封装，学生难以理解有限元的计算原理，较难对相关模块作进一步的科研开发，限制了教学和科研的使用。除上述软件外，也有不少开源的有限元软件，如Elmer、ParaFEM和Freefem++。这些软件不但对公众开放源代码，而且可靠性较高，相关模块的说明文档也较丰富，非常适合于教学和科研。经过长时间的比较测试和应用，发现Freefem++语句非常简洁，只需要将原方程转换成弱解形式，使用Freefem++很容易编写有限元程序，是最接近有限元的“计算语言”[8-9]。但该软件也有一个弊端，没有极坐标系的相关程序单元可供使用，仅提供直角坐标系的。为了解决这个问题，基于直角坐标系的程序单元，文章推导了极坐标系梯度与法方向的转换公式，并应用于具体案例中，以期为Freefem++极坐标系的有限元程序设计和教学提供参考。

1 定解问题及弱解形式

问题求解区域如图1所示。半径R=1的1/4圆域Ω，圆心为O，边界区域依次为Γ1、Γ2和Γ3。该区域的函数u(r,θ)满足如下的泊松方程：

(1)

其中f表示作用力或源，r和θ分别表示径向和横向坐标，Δ表示拉普拉斯算符，有如下关系：

(2)

问题(1)的边界条件，如图1所示，满足关系：

(3)

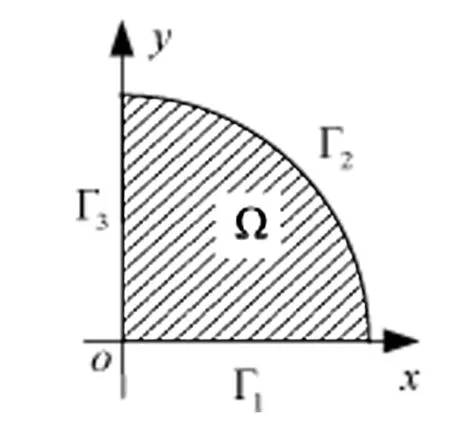
图1 半径R=1的1/4圆域Ω及其边界，其中O表示圆心

(4)

其中Γ表示求解区域Ω的边界，∂u/∂n表示u在法方向的梯度，▽表示梯度算符。

2 不同坐标系梯度和法方向转换

(4)式在计算时，需要用到极坐标系的梯度与法方向导数。极坐标系的梯度算符有如下关系：

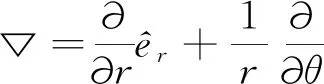
(5)

其中êr和êθ分别表示径向和横向单位矢量。(4)式表明诸如(1)式和(3)式的强解问题，可以用(4)式的弱解方程来求解，而且(4)式直接包括了强解问题的边界条件，因此，(4)式具有很高的实用价值。由于本问题中没有待求函数在边界上法方向的梯度，需要对(4)式的边界积分项进行处理。根据方向梯度的定义，可得：

(6)

依据(3)、(4)和(6)式，可以求出边界项积分。若(x,y)和(r,θ)分别表示直角坐标和极坐标，(,)和(êr,êθ)分别表示直角坐标系和极坐标系的单位方向矢量，考虑到：

(7)

可得：

(8)

(9)

3 应用Freefem++求解定解问题

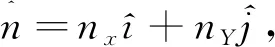
其中macroGrad(u)用于定义极坐标系中，待求函数u的梯度分量；macroLap(u,v)表示(4)式中双线性项u·v；macroNrq用于定义法方向在极坐标系的坐标分量；BC2(u)表示(4)式中边界积分项的法方向梯度∂u/∂n;problemlaplace(u,v)用于定义(4)式的弱解问题，其中on(1,u=0)和on(3,u=0)分别表示(3)式中的第一边界条件。应用图2所示代码，数值计算结果如图3(a)所示。根据数学物理方法[11-12]，可知定解问题(1)和(3)的解析解为u=rcosθsinθ，其结果如图3(b)所示。数值解减去解析解，其平方值的分布如图3(c)所示。很显然，数值结果图3(a)与解析解图3(b)的分布一致，其误差分布除坐标原点外，其它地方的误差最小，误差分布也较均匀。坐标原点处的误差，来源于(1)式中，源f含有r，在圆点处会发散，导致数值解在圆点处不稳定所致。

图2 基于Freefem++语言格式的有限元程序代码

图3 有限元数值解(a)，解析解(b)，数值解与解析解之差的平方(c)

4 结语

计算物理在理工科类专业中具有重要作用。特别是随着科学技术的发展，有限元软件得到普及，培养这方面的专业技术人才，既是教育发展方向，也能满足市场需求，对提升高校竞争力至关重要。目前市场上有很多有限元软件，大多口碑较好的是闭源商业化的，模块不对外开放，不利于教学和科学研究的应用。为了克服这个问题，众多科研机构开发了一系列有限元开源软件，使得有限元方法在教学和科研中的应用成为可能。在众多开源软件中，Freefem++类似于C++，语句简洁，容易上手，非常适合于教学和科研，在工程实践中也有相关的应用。但该软件有一个弊端，没有极坐标系的相关程序单元供使用，软件提供的仅有直角坐标系的相关程序单元。针对该问题，本文分析了直角坐标系与极坐标系中梯度与法方向的转换关系，导出了极坐标系的弱解形式，设计出基于Freefem++的有限元程序。并成功地将该程序应用于1/4圆域的泊松方程中，发现数值计算结果与解析解一致。除坐标原点外，数值解与解析解两者间较小的误差，显示了较好的一致性和稳定性，验证了本文推导的极坐标系梯度和法方向计算公式的合理性。