柳州市白沙大桥西岸引道立交异型箱梁分析

唐军斌

（柳州市市政设计科学研究院，广西 柳州 545006）

0 引言

城市立交桥是一种现代化桥梁工程，以多层道路在三维空间上形成立体交叉为基本特征。为满足交通需求及提升城市景观，城市立交桥的设计与建设需在符合相应建设标准的前提下，力求行车舒适、线型流畅、外形美观。在主线与匝道、匝道与匝道连接段，常需设置几何不规则的异型结构。由于现浇箱梁结构具有整体性好、适应性强、外形美观等特征，使得其在异型结构上得到广泛的应用。

有别于常规梁式箱梁，异型箱梁空间受力较为复杂，弯扭耦合作用明显，存在翘曲与扭转的双力矩效应[1]。常规的单梁分析法已无法准确计算结构的内力与应力，需采用有效的三维空间模型进行受力分析。随着计算理论与计算软件的不断完善，空间梁格法、薄壁箱梁法、三维实体单元法等有限元分析方法应运而生。

1 工程概况

1.1 项目概述

柳州市白沙大桥西岸引道立交作为潭中半岛中北部交通枢纽，承担着串联河东片区、潭中半岛以及白露片区等3个重要区域高交通量、高中转量的交通任务。本工程共分为引道主线、跃进路改造段及白沙路改造段3个主体部分。其中引道主线包括白沙大桥西岸引道-跃进路及白沙大桥西岸引道-白沙路2个重要的节点立交。立交区内共设桥梁10座，其中主线桥1座（长170.1 m），闭合环道桥（圆盘）1座（长266.721 m），匝道桥8座（总长1 124.2 m）。

1.2 结构设计

立交桥Y匝道与J匝道连接段为分衩结构，结构采用3×20.2 m钢筋混凝土变宽连续箱梁桥。桥宽为9.4～16.2 m，箱室数量由2个过渡为3个，为异型空间结构。箱梁梁高1.6 m，悬臂长2 m，顶、底板厚分别为0.25 m、0.22 m，腹板厚度由0.4 m过渡至0.6 m，采用C45钢筋混凝土。

箱梁平面布置图、箱梁断面布置图见图1、图2。

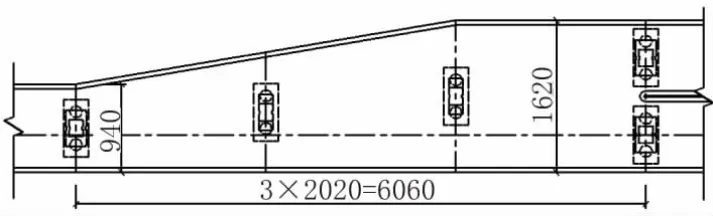
图1 箱梁平面布置图（单位：cm）

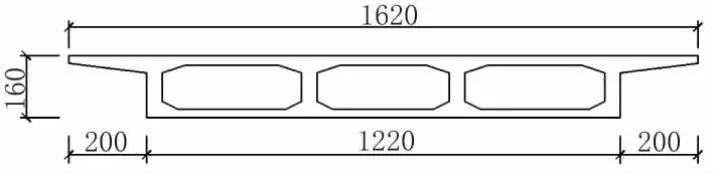
图2 箱梁断面布置图（单位：cm）

2 设计分析方法

对于单箱多室梁桥的空间有限元分析，在桥梁设计工作中较为简便、高效且满足工程计算精度的方法主要有空间单梁法、薄壁箱梁法、空间梁格法和三维实体单元法[2]。这4种有限元分析方法比较见表1。

表1 有限元分析方法比较表

由表1可知，空间梁格法可有效地计算异型箱梁的空间受力，建模简便的同时可达到工程上允许的精度，较其他方法有较好的优越性。

2.1 梁格法基本原理

莱特福和绍柯最先提出桥梁上部结构梁格计算法的原理，后来形成了以英国学者汉勃利为代表的剪力-柔性梁格法。其基本原理是将上部结构用梁格等效，假定上部结构某区段内的弯曲刚度和抗扭刚度集中于最邻近的等效梁格内，实际结构纵/横向刚度分别集中于纵/横向梁格构件内[3]。等效的原则为在承受相同的荷载情况下，梁格模型与实际结构具有相同的挠曲，弯、剪、扭等内力等于该梁格所代表的实际构件部分内力。本方案较适用于分格式上部结构，对多箱室箱型截面，当剪力多由腹板承受且横梁刚度较小时，有较好的工程意义。

2.2 梁格划分方法

划分梁格模型的正确与否，影响结构分析的准确性。基于其计算原理，梁格划分可采用以下原则[4]：（1）纵横梁重合于实际受力位置；（2）纵横向梁格间距小于有效跨径的1/4,截面突变处则减小间距，且纵横梁间距宜相近；（3）斜交角度小于20°的简支上部结构，可采用直交梁格分析，而连续梁及斜交角度较大时需要按实际结构建模；（4）纵横梁宜构成直角，斜交方向受力时可按实际角度建模；（5）梁格划分应使各分部截面形心轴位置与总体截面位置相一致。

3 结构分析

3.1 模型建立

根据本工程实际结构，采用Midas/Civil软件进行建模分析。全桥结构离散时，综合考虑跨径、顶底板及腹板加厚、断面布置及精细化要求，纵向1～1.5 m划分1个单元，横向单元宽度为该节点所代表的前后纵向单位宽度的一半之和。合计划分为395个节点，487个单元。分为4条纵梁，7条实际横梁，以及若干虚拟横梁。结构离散模型及三维模型见图3、图4。

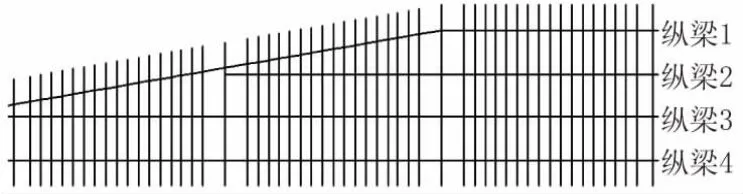
图3 结构离散模型

图4 结构三维模型

3.2 荷载分析

根据桥梁实际静力荷载工况，结构考虑以下受力状态：（1）自重；（2）二期恒载（桥面系部分）；（3）温度荷载（系统温度+温度梯度）；（4）支座沉降（-5 mm）；（5）收缩徐变；（6）移动荷载（城 -A 级车道荷载）。由于每个梁格单元纵横向宽度的差异性，要精细地加载桥面系二期恒载，工作量庞大，对于设计工作而言效率较低。结合工程经验，将二期恒载折算为相应梁格单元的自重，采用提高自重系数的方式进行加载。对于移动荷载，车道荷载加载在横向联系梁上。由于桥梁过渡段车道数为变化值，需考虑不同车道布置下的活载效应，取最不利值。

3.3 分析结果

对结构进行承载能力极限状态及正常使用极限状态验算，提取关键截面支点、跨中、1/4跨处抗弯、抗剪及裂缝验算结果，如图5～图7（图中L均为跨长）所示。

图5 关键截面抗弯验算表（Mn为抗力值；rMu为内力值）

如图5～图7所示，结构抗弯、抗剪及裂缝验算均符合《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62—2004）中要求：最不利组合下的结构内力均小于结构抗力，裂缝计算值均小于0.2 mm限值。

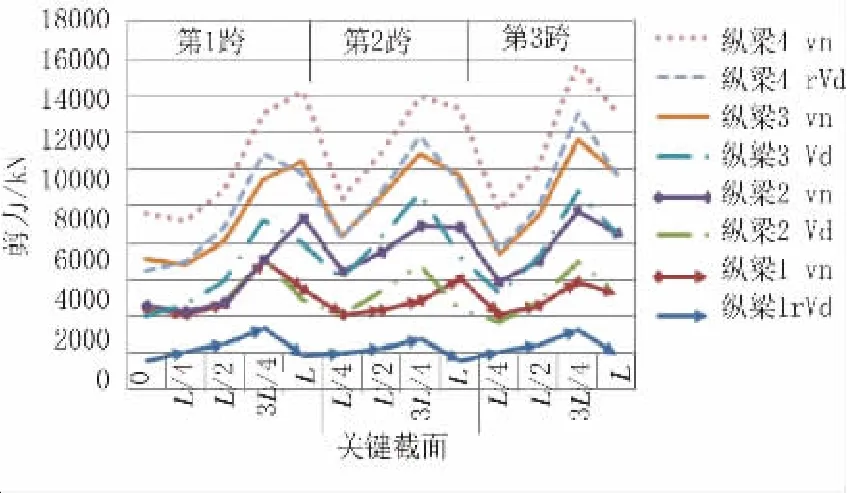
图6 关键截面抗剪验算表（vn为抗力值；rVd为内力值）

图7 关键截面裂缝验算表（W-tk为裂缝值；W-AC为限值）

综合上述分析结果可知，由于弯扭耦合作用的影响，同时因构件不对称造成的纵梁计算长度不同，异型箱梁在荷载作用下，各腹板纵梁受力状态差异较大。结构设计时，需针对各腹板进行差异化处理，避免各腹板采用相同配筋布置的“一刀切”设计理念，力求安全、经济。

4 结语

（1）由于采用的是实际横梁结构，可获得较为真实的横梁受力状态。相比单独进行横梁计算的方式更符合实际。

（2）异型箱梁在箱室数量变化处存在相交腹板时，受力较为复杂，梁格法尚不能精确计算，需结合三维实体单元进行分析。

（3）梁截面温度梯度引起的次内力较大，鉴于纵横向梁格单元尺寸的不均匀性，加载温度梯度荷载时需根据单元横向宽度逐一设置，以保障内力计算的准确性。

（4）由于车道数目非恒定值，桥面布置车道荷载时，宜根据不同跨间车道实际数量进行分区段加载，以求得最真实的活载效应。