溢洪道流量系数计算的相关性分析
——基于人工神经网络模型
2019-08-21陈茂聪
陈茂聪
(梅州市威华水利水电建设工程有限公司,广东 梅州 514299)
溢洪道主要作用是为保证大坝等水工构筑物宣泄规划库容所容纳不了的洪水。溢洪道构筑有多种构筑形式,如开敞式或带有胸墙进水口的溢流泄水建筑物。虽然,溢洪道的使用频率不高,但却是水利系统必不可少的建筑物。溢洪道按泄洪标准和运用情况,分为正常溢洪道和非常溢洪道。前者用以宣泄设计洪水,后者用于宣泄非常洪水。溢洪道除了用于蓄水、节能、灌溉、防洪等用途外,还可用于水库中一定水位的蓄水[1]。鹰眼形的溢洪道使水库中多余的水流向下游[2-3]。
国内外许多研究人员对溢洪道进行了数值模拟和实验研究[4-7]。ANN模型也常用于溢洪道的研究。孙涛[8]研究了滑跳式溢洪道冲刷深度预测问题。研究表明,计算机模型运算准确性较好、效率高,可以取代基于方程式的传统方法预测设计。宁景昊[9]运用数值模拟分析对比溢洪道连续性挑流鼻坎与差动式挑流鼻坎在设计工况下的水力特性变化规律验证差动式挑坎的优越性。武华宝[10]应用Realizable k-ε湍流模型、VOF法模型追踪自由表面和非结构网格区域离散进行处理,得出VOF模型能较好的反映出溢洪道进水口的压力场分布,与模型试验的结果吻合较好的结论。邹璐[11]采用Multi-Block和FAVORTM技术结合的方法进行网格划分,运用FLOW-3D软件对台阶式溢洪道水流进行数值模拟,研究结果显示数值模拟结果与己有的试验结果基本吻合。
诸多学者研究了神经模糊方法在估算阶梯溢洪道水流流态的适当消能值时的适用性和准确性,建立了多元回归方程,神经模糊模型比回归方程更成功。洪礼聪[12]建立用于识别尾水管涡带状态的卷积神经网络模型,通过三种时频图像识别率对比分析,得出具有更高低频局部分辨能力的小波系数云图更适于作为本文提出方法的模型输入图像,其识别率可达到94.63%。霍俊波等[13]构建了基于径向基(RBF)神经网络算法的桥墩局部冲刷深度预测模型,并分析了模型预测结果的误差分布。张娜[14]运用神经网络对水位流量关系率定,仿真结果表明BP神经网络流量预测模型方精度最高。本研究的目的是探讨人工神经网络模型对溢洪道流量系数的估计能力。
1 材料与方法
1.1 材料
为了方便操作,自行设计了实验装置。该实验装置如图1所示:有机玻璃粘合制成水槽。其尺寸为宽7.5 cm,深15.0 cm,长5 m。计算通过不同水头的溢洪道流量。水槽采用闭环水系,流量由恒头水箱供给,流量可由阀门调节。透明水槽也可观察到水流状况。用沿水槽放置的测量装置测量的深度精度为1 mm。使用尺寸为63 cm×67 cm×72 cm光滑塑料罐测量流量,溢洪道模型如图2所示。

图1 水槽总图
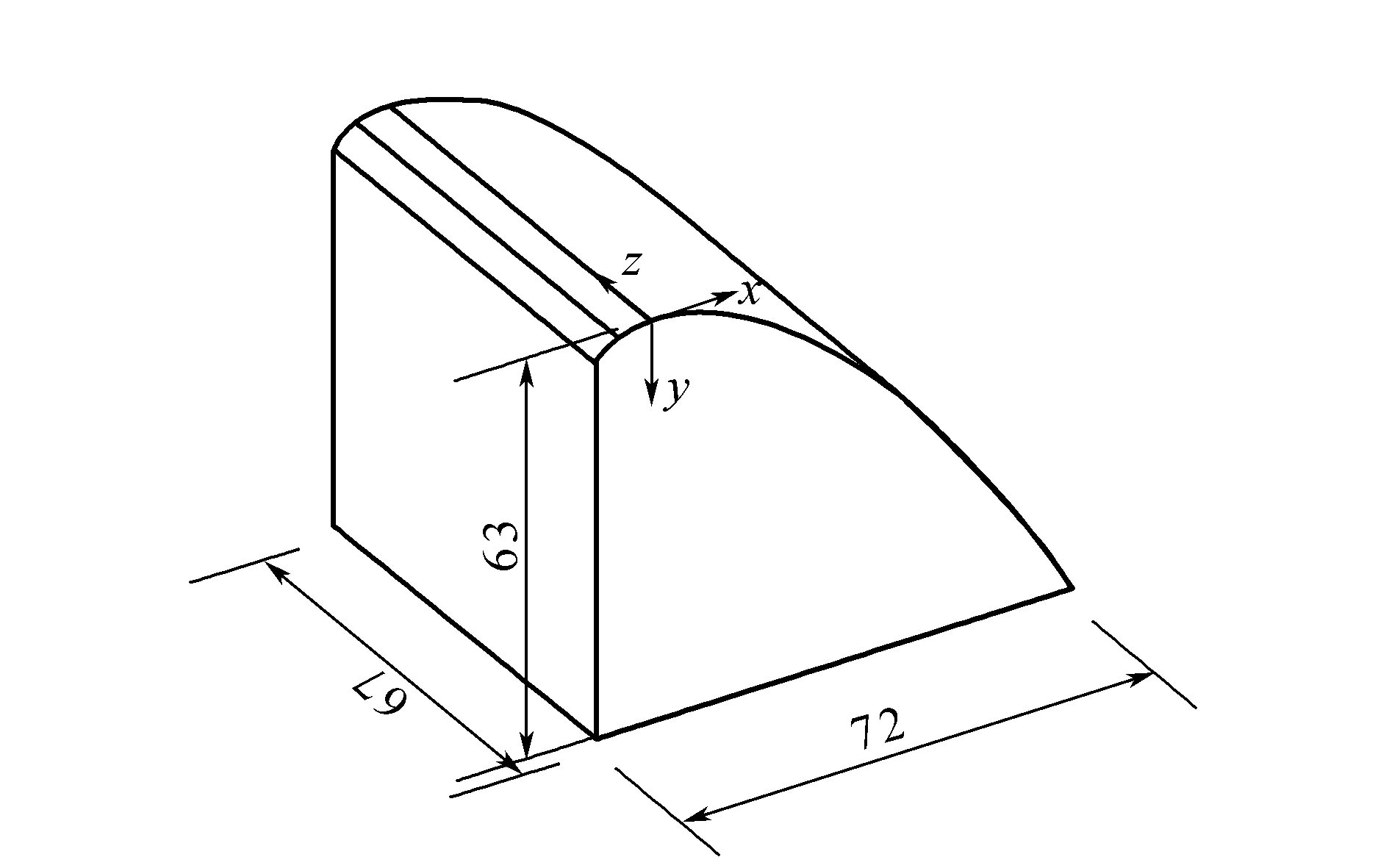
图2 溢洪道模型(单位:cm)
1.2 方法
根据相关文献,理想形式的溢洪道如图3所示[3]。

图3 溢流口的标准顶部剖面
溢洪道的下游可由式(1)定义:
(1)
式中:X,Y分别为距原点的水平方向和垂直方向距离,m;K和n是常数,取决于上游倾斜和速度;H0是设计水头。溢洪道上的流量可以用式(2)计算:
(2)
式中:Q为流量,m3/s;C为流量系数,m1/2/s;L为波峰长度,m;H为水头,m。现有总水头的流量系数根据不同水头的流量系数经验模型确定。
人工神经网络(Artificial Neural Network,ANN ),从上世纪80年代以来,人工智能领域兴起,至今仍是各行各业研究热点[15]。人工神经网络从信息处理角度对人脑神经元网络进行数学抽象,从而构建模型。按不同的连接方式组成不同的网络。ANN是一种运算模型,由大量的节点(或称神经元)之间相互联接构成[16]。每个节点代表一种特定的输出激励函数(activation function)。每两个节点间的连接都代表一个对于通过该连接信号的加权值。网络的输出网络的连接方式,权重和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近,也是对一种逻辑策略的表达。人工神经网络(ANN)系统由输入层、隐藏层和输出层3层组成,即多层感知器 (MLP)(见图4)[17]。
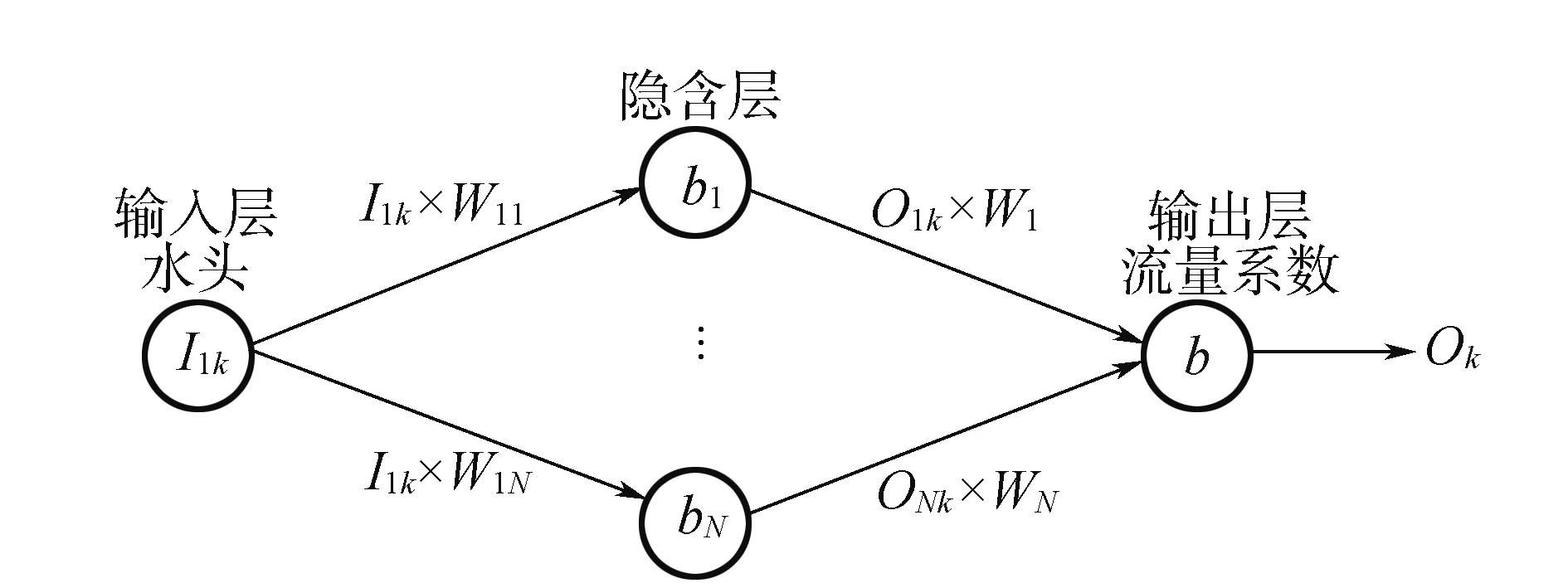
图4 多层感知器的结构
用于预测的3层后向反馈式神经网络的数学表达式如式(3)、式(4)所示:
(3)
(4)
式中:f1为隐藏层的激活函数;Ii k为第k个采样点的第i个输入;Oj k为隐藏层第j个节点的输出;Wi j和Wj是控制层与层之间连接强度的权重;bj和b分别为用于调整隐藏层和输出层平均值的偏倚。
2 结果与讨论
对不同流量下的溢洪道水深进行了实测。由水箱测定各水头的流量,计算流量系数。通过放置时间完成该过程,直至灌装至一定体积。通过式(2)计算流量系数并对实验和分析结果进行了比较。
在MatLab软件中,将不同水头获得350个实验数据集合,250个数据集划为训练集,其余50个数据集用于验证集,剩余50个数据集为测试集。采用前馈反向传播神经网络模型和标度共轭梯度法 (SCG)进行建模。在神经网络模型中采用3层神经网络结构,即1个输入层、1个隐藏层和1个输出层。人工神经网络结果与实验结果的关系如图5所示。由图5可以看出,训练集与目标数据相关性,R=0.993,表明网络训练集模型输出数据与目标数据相关性较好,验证集、测试集相关系数分别0.891、0.966,表明BP仿真神经模型稳定性较好。
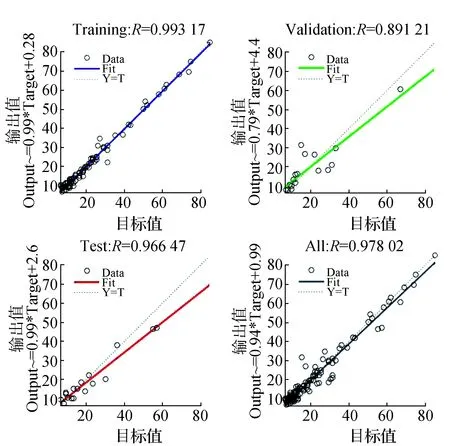
图5 实验结果与BP神经网络预测模型拟合结果
3 结 语
正确设计的溢洪道将能够高效、安全地将洪水流引至大坝下游。因此,准确地确定水体的流量对水体结构物具有重要的意义。人工神经网络模型可以作为确定流量系数的一种替代方法。利用人工神经网络模型,在不使用图解和方程的情况下,可以快速确定适当的系数。
