水位下降作用下堤防稳定性数值模拟研究
2019-08-21吕雪超王理想刘发智
吕雪超,王理想,刘发智,韩 雷
(1.哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001; 2.黑龙江省水利科学研究院,黑龙江 哈尔滨 150080)
水库库岸边坡稳定性在水位骤降工况下的研究比较成熟,对水位下降条件下堤防稳定性的研究同样具有重要的意义。高骥[1]将堤坝内饱和区和非饱和区耦合在一起,构成整体的分析模型。朱伟[2]研究了河堤内非稳定渗流的实测与分析,得出浸润线的变化趋势。陆彦[3]研究河道水位降落对边坡稳定的影响,得出边坡稳定与渗流方向有关。赵宇坤[4]通过建立有限元渗流模型得出水位骤降情况下的堤岸稳定状态。刘杰[5]等提出接触冲刷水力坡降。韩雷[6]通过对黑干砂性土物理特性试验,指出砂性土渗透性良好,不易压实,完工后对工程质量影响较大。本文以二元混合堤为研究对象,利用岩土工程有限元数值分析软件GEO-Studio,在前人研究的基础上,主要研究长期高水位浸泡作用下混合堤在不同下降速度下的堤防渗流与抗滑稳定性。
1 工程概况
以松花江流域某混合堤段为研究对象,堤防高6 m,堤顶宽8 m,堤身宽47 m,迎水坡坡比为1∶3,背水坡坡比为1∶3.5,上层级配不均匀砂性土,下层黏土。
渗流分析使用程序SEEP/W,有限元网格划分采用四边形与三角形模式,总共696个单元,如图1所示。堤防20~50 a设计洪水标准,选取设计洪水位(水位高度4 m)作为对象分析,模拟2.500 cm/s(骤降)、0.100 cm/s(快降)和0.003 cm/s(缓降)不同下降速度工况下堤坡稳定性分析,计算时间为680 h。
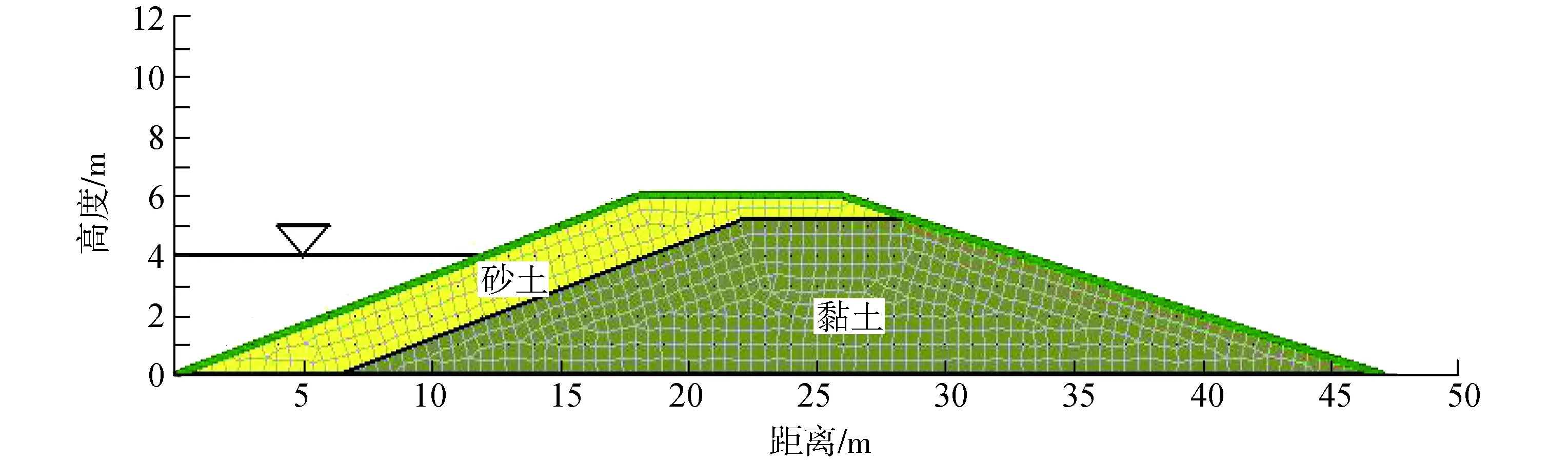
图1 混合堤段断面边坡分析有限元模型和网格划分

材料类型干密度/(g·cm-3)黏聚力/kPa内摩擦角/(°)饱和渗透系数/(cm·s-1)不均匀系数砂性土1.53035.00.036.5黏土1.49408.50.000 0027.2
2 有限元法渗流分析
2.1 有限元法原理
有限元法是把连续体离散化为有限个单元的集合体来进行研究,引用变分原理对研究问题建立模型,推导出近似解的一组方程,最后归结为求解多阶系数矩阵的线性方程组,利用计算机在矩阵分析和数值方法的基础上进行所需要精度的计算。
2.2 数学模型:
二维渗流的数学模型为:
(1)
式中:Ss为单位贮存量;Kx为x方向渗透系数;Ky为y方向渗透系数;h为水头高度。
Ss=ρg(α+nβ)
(2)
式中:n为土体的孔隙率;α骨架颗粒的压缩性;β为水的压缩性;ρ为水的密度;g为重力加速度。
基本方程的求解需满足定解条件:
(1)边界条件分为水头边界条件见式(3)和流量边界条件见式(4)。
h|Γ1=h(x,z,t)
(3)
(4)
(2)初始条件见式(5)。
h|Γ1=h(x,z,t)
(5)
数值模拟中定义水位下降迎水坡为水头边界条件,背水坡定义为不透水边界,水位下降分析的结果代入堤坡稳定性分析中,采用Morgenstern-Prince极限平衡法求解水位下降时堤坡稳定系数。
3 混合堤渗流模拟结果分析
3.1 不同下降速度浸润线变化
水位缓降(图2)初始阶段,堤内水位响应稍有滞后,孔隙水排出较慢,而水位快降(图3)和骤降(图4)阶段,水位下降速度快,使得堤内饱和孔隙水来不及排出,堤内残余的孔隙水压力变大,土体的抗剪强度变低,堤内渗透坡降变大,顺坡下滑方向的渗流作用力也变大,将对堤防渗透和边坡稳定性产生不利影响。

图2 缓降(0.003 cm/s)浸润线变化图
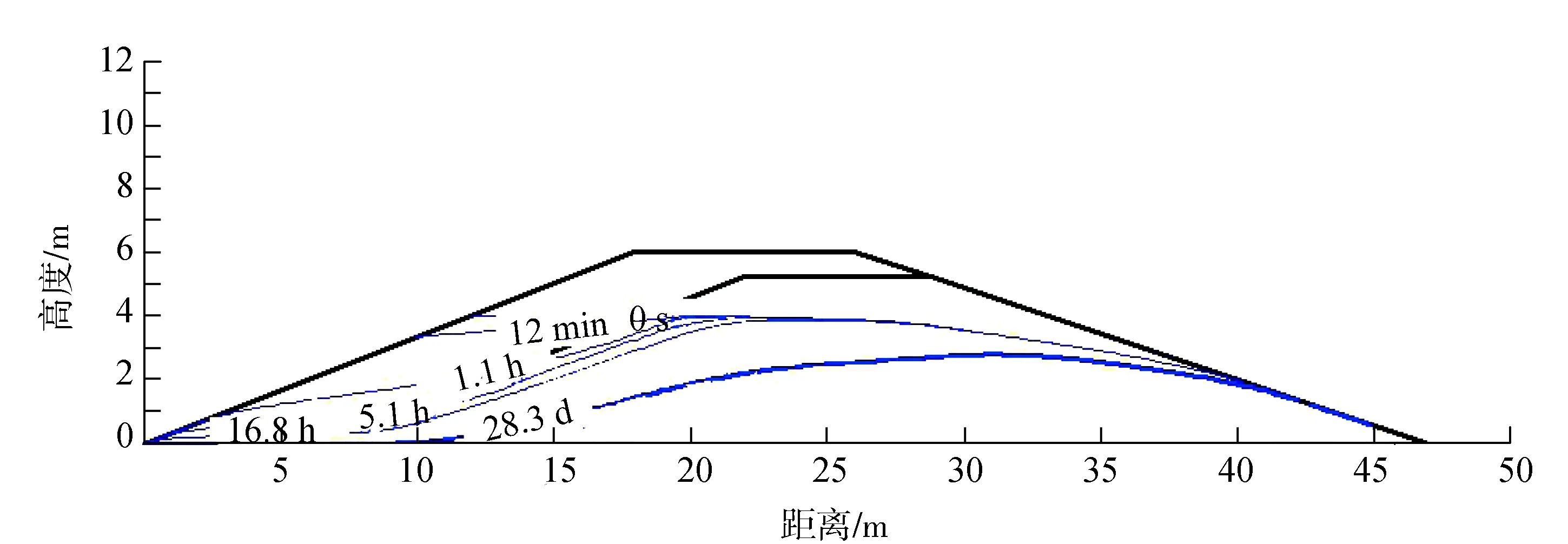
图3 快降(0.100 cm/s)浸润线变化图
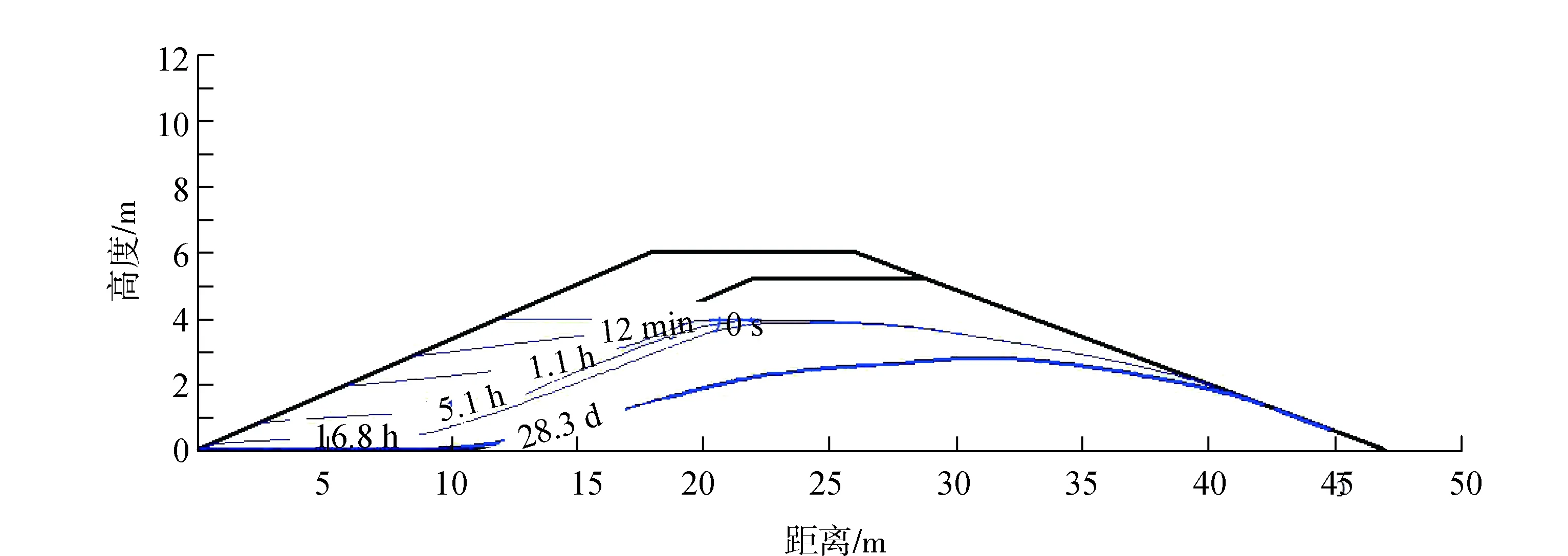
图4 骤降(2.500 cm/s)浸润线变化图
3.2 XY方向渗透坡降
骤降条件下渗透坡降见图5。
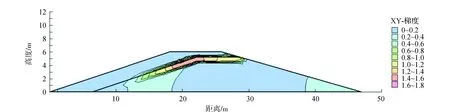
图5 骤降(2.500 cm/s)5.1 h后XY方向渗透坡降图
根据《堤防工程设计规范》[7](GB 50286—2013),无黏性土的允许坡降,见表2。
根据室内土的物理试验,各层土的物理性质见表3。

表2 无黏性土的允许坡降

表3 现场土层的物理性质
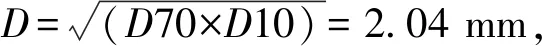
当最大坡降大于临界坡降,会发生流土破坏,泥沙颗粒会被水流带走。流土是否发生的判别条件是i≫Ic r。李广信[8]提出土中水引起的渗透破坏-流砂,相对于流土范围更广一些,也可能发生在任何方向,并且比流土的临界水力坡降要小。考虑XY方向坡降,表4~表6为不同条件下水位下降不同时刻的最大水力坡降和可能发生的破坏类型。
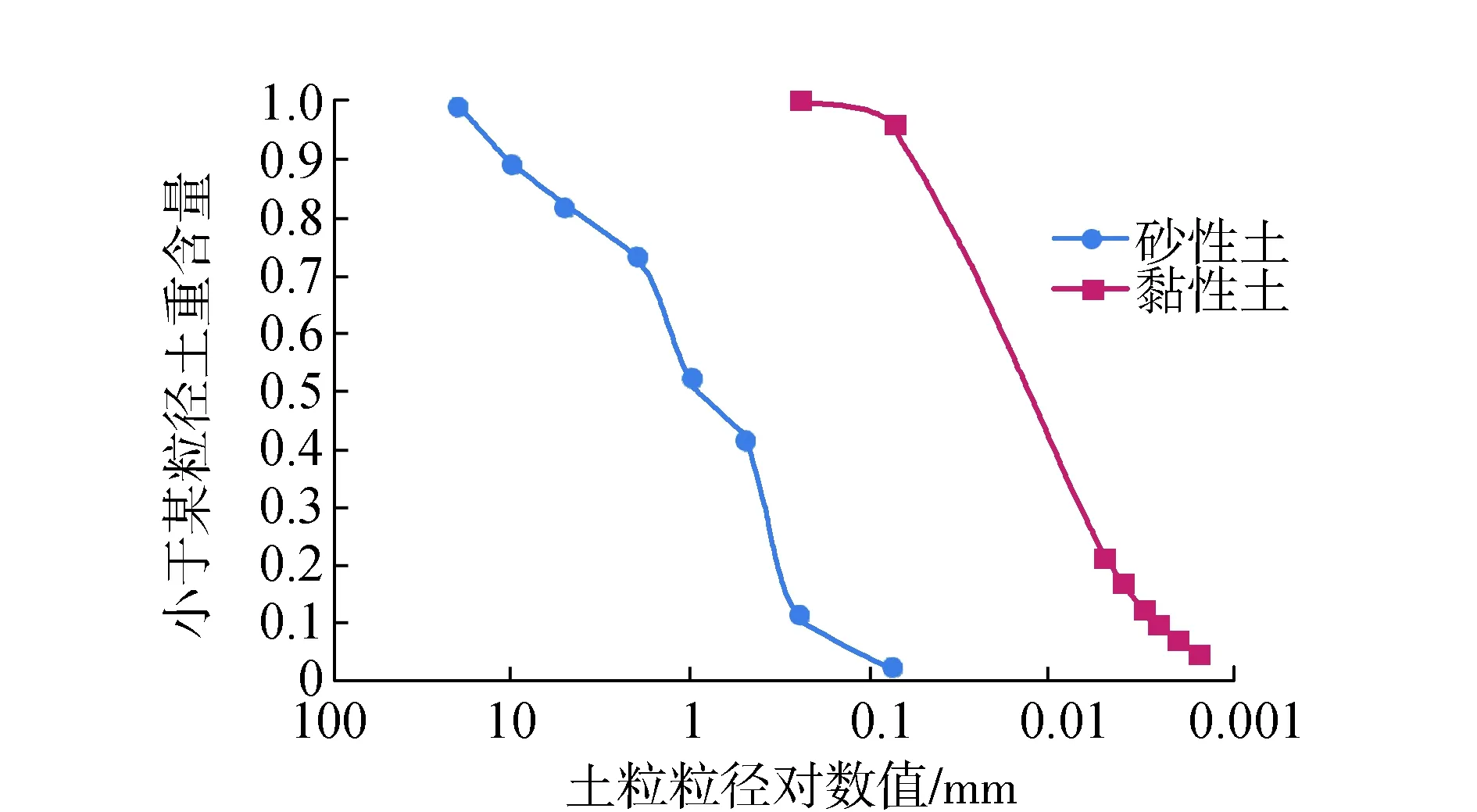
图6 现场迎水坡填筑料颗粒分析曲线

表4 骤降条件下堤防比降和可能发生破坏类型

表5 快降条件下堤防比降和可能发生破坏类型
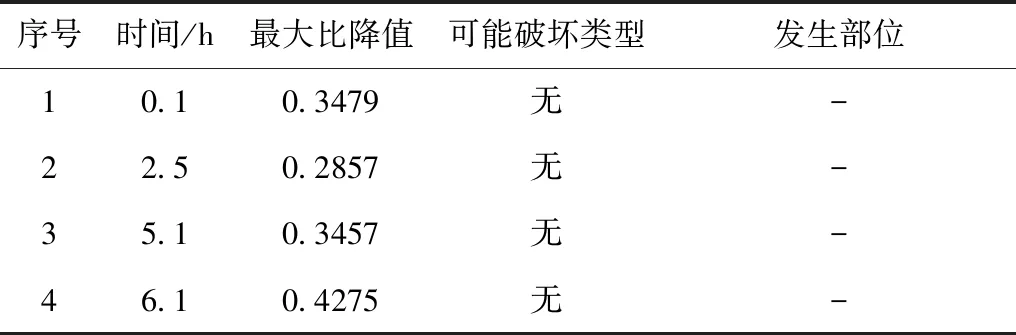
表6 缓降条件下堤防比降和可能发生破坏类型
水位骤落后堤坡渗透坡降较高,在非稳定渗流条件下,渗流方向由内向外。水位在降落后短时间内,渗透力的增加将会对堤坡稳定性产生影响,同时接触面材料粒径差别较大,促使接触面土体滑动。由表4~表6可知骤降工况下堤防发生渗透破坏,主要集中发生在迎水坡坡脚及砂性土和黏土层接触面;快降工况下,发生流砂和接触冲刷的可能性较大,集中在迎水坡砂性土和黏土层接触面;缓降对堤防渗透破坏的可能性较低。
3.3 堤坡稳定系数
由图7可知,不同下降速度下,骤降、快降和缓降工况下堤坡稳定性变化规律比较一致。随着孔隙水压力消散,稳定系数也发生较大的变化,呈现先下降,然后逐渐增大最终趋于稳定状态。速度越快最初的稳定系数越小,但最终的稳定系数是相同的,在堤防合理设计范围内,不同下降速度引起滑坡的可能性较低。
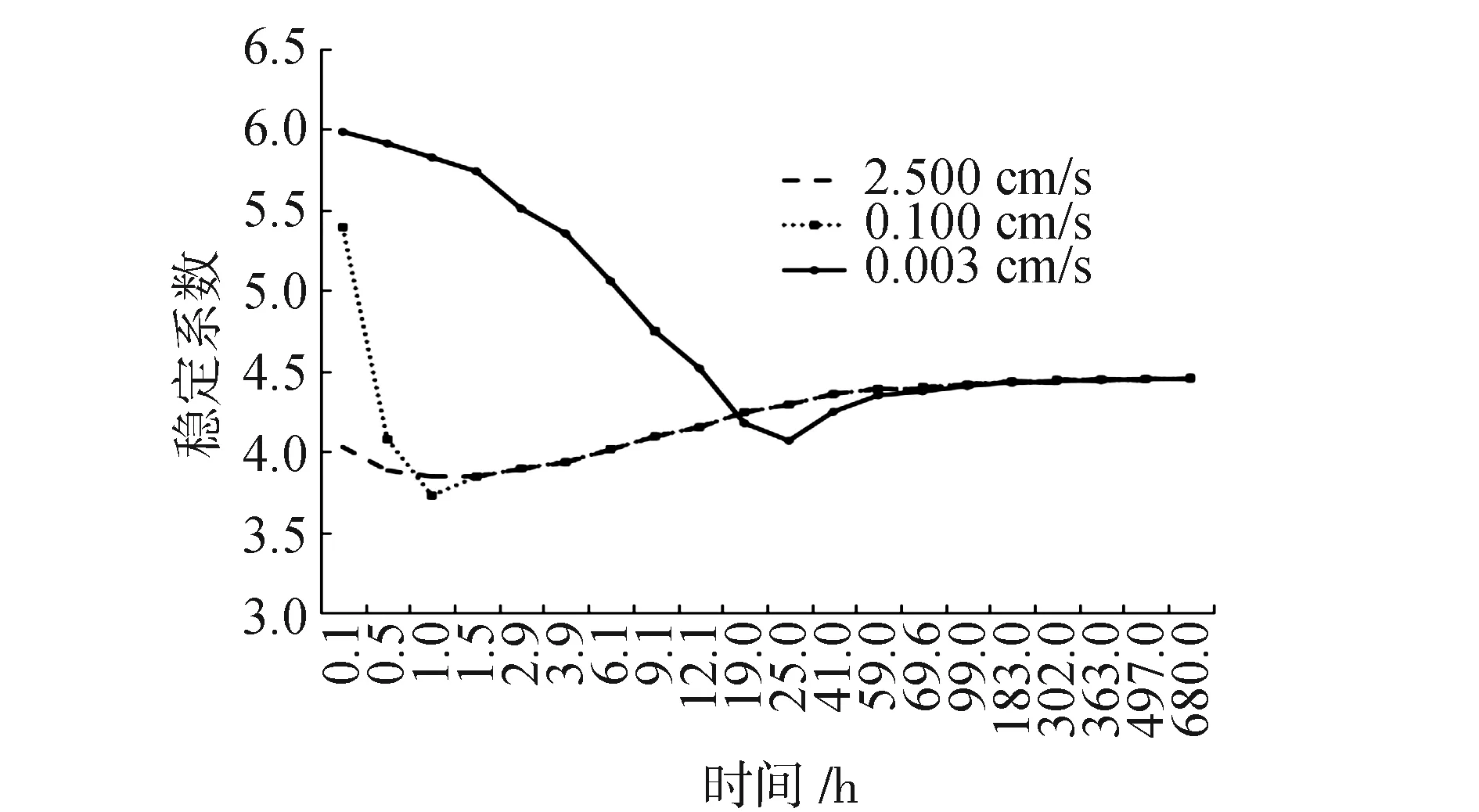
图7 不同下降速度稳定系数图
水位降落之初,堤坡内部的水来不及排出,在坡体内部产生不稳定渗流,继而产生动水压力,对边坡产生不利的影响,使堤坡的稳定系数降低。随着时间的增长,坡体内水不断的排出,坡体内的渗流作用力不断减小,坡体的稳定系数不断增加。
4 结 论
本文以典型混合堤防为例,结合地质条件,建立渗流有限元数值模型,对设计洪水位长期浸泡条件下的二元混合堤防进行数值模拟研究,得到以下结论:
(1)水位骤降过程中,水位下降初始阶段,堤坡迎水侧可能发生流砂渗透破坏,随着孔隙水压力消散,砂性土与黏性土交界面处会发生流砂和接触冲刷渗流破坏;快降过程中主要在砂性土和黏性土交界面处发生流砂和接触冲刷;缓降发生渗透破坏的可能性较低。
(2)通过计算得出,下降速度对堤防稳定性和渗透稳定性有决定性的影响。下降速度越快,边坡内残余的孔隙水压力就越大,土体抗剪强度越小,堤防最初的稳定系数越小。堤防稳定系数随着水位下降呈现先减小后增加,最终趋于稳定一致的状态。在堤防稳定性合理的设计范围内,不会产生滑坡、崩塌现象。
(3)这里只对影响堤坡稳定性的下降速度进行研究,还有很多因素可以继续研究分析,如降雨、堤防土体参数等对堤坡稳定性不利的因素,从而为水利工程混合堤防建设提供参考意见,避免不利因素影响。
