基于ARMA模型下的我国消费价格指数预测

(四川大学 四川 成都 610065)

一、文献综述

杨坚(2014)认为CPI数据中存在季节性因素和周期性因素影响，并采用了ARIMA模型对12个月内的CPI数据进行了分析，实证表明了存在季节性与周期性因素影响。王维(2012)采用了混沌理论，针对CPI数据中存在的非线性特征进行了相空间重构，利用混沌网络算法构建了短期内CPI的预测模型，并取得了较高的预测精度。范敬雅(2016)将CPI时间序列分解成细节序列与近似序列，针对近似序列采用SVM模型进行了拟合预测，有效提升了预测精度。孙冠华(2018)在BP网络模型，RBF网络以及和方法对传统的通过ARMA模型分析预测居民消费价格指数进行了改进。

二、模型建立

(一)数据选取

本文从中国国家统计局网站选取了2014年1月至2019年5月的CPI的实际月度数据的同比增长指数数据。同比增长是指以上年同月为基期，展示出报告期与基期的水平之比，能够很好的反映出指标的发展趋势。

(二)数据的平稳性检验

图一为2014年1月至2018年12月的我国居民消费价格指数数据，建立模型前，需要对该序列数据进行单位根检验，判断该序列数据是否是平稳的。通过使用eviews7.0软件计算其ADF结果如下图，如图二所示，ADF检验的t统计量小于1%显著性水平下的临界值，故该序列数据是平稳的，建立模型之前不需要进行差分

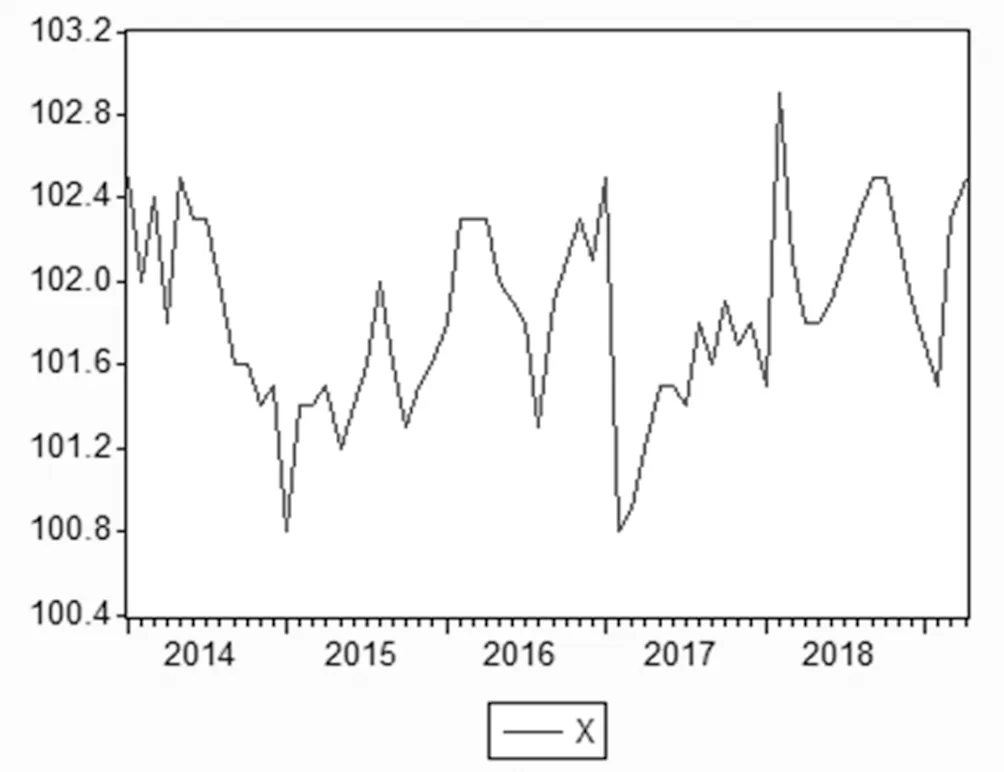
图一

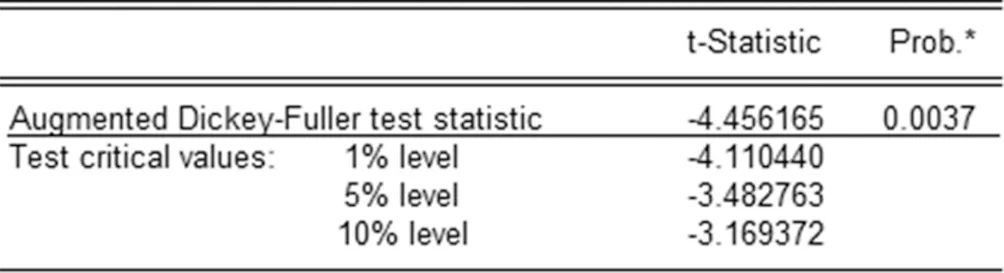
图二

(三)模型建立

经过对该CPI序列的自相关和偏自相关图的分析，初步建立模型ARMA(12，1)，ARMA(2,1)、AR(2)，运用最佳准则函数定价法进行反复筛选，综合考察模型的整体拟合效果，确认模型如下

Xt=101.83+0.43Xt-2+εt+0.55εt-1

(四)模型平稳性检验

为了检验模型的平稳性，需要对模型特征根进行检验。若特征根的倒数都小于1，则表明本文建立的ARMA(2,1)模型是稳定的。经检验，特征根都落在单位园内，本文建立起来的模型是平稳的。

(四)残差序列的独立性检验

在模型参数估计后，模型残差序列还需要进一步检验是否为纯随机序列。若残差序列不随机，则说明残差序列中的存在有用信息可能被遗漏的情况，需要重新设定模型。通过对残差序列的检验发现，Q统计量检验通过，残差序列是纯随机的。即ARMA(2,1)从数据中充分提取信息是合理的。

(五)模型的预测

图三是通过ARMA(2,1)模型得到的样本预测值与实际值的拟合图可以看出，模型的预测精度整体良好。

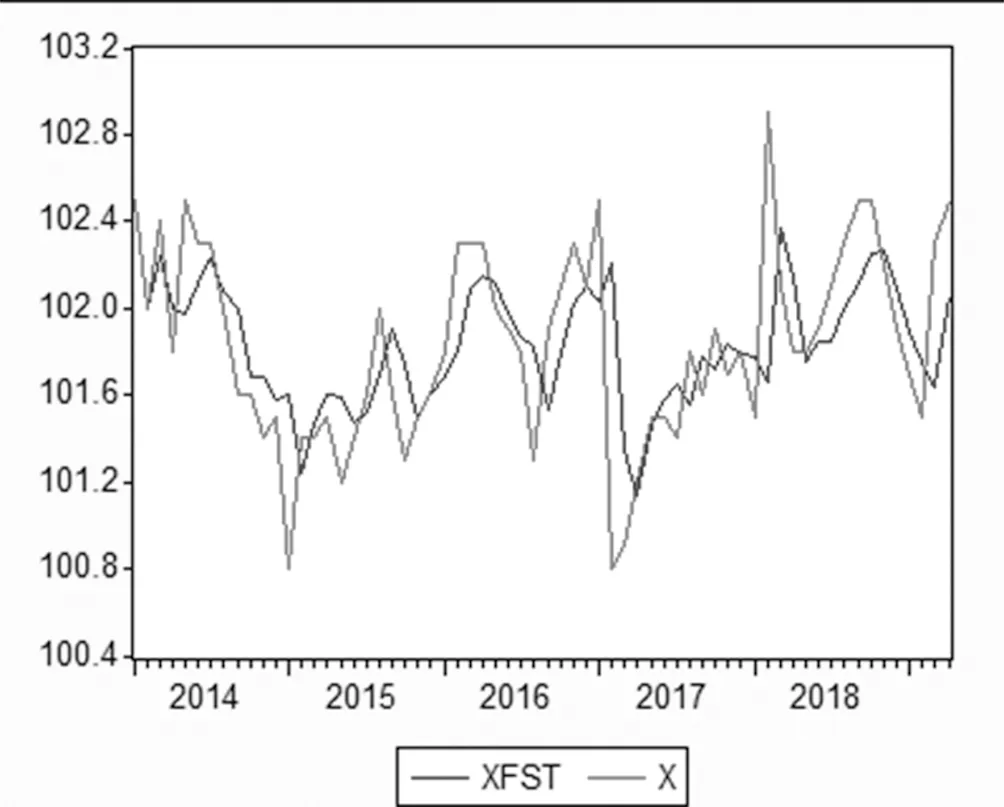
图三

为了进一步分析研究全国居民消费价格指数的趋势，我们利用所建立的ARMA(2,1)模型对2019年5月至12月的CPI指数做出了样本外的动态预测。

表一

三、结论

通过上述的分析和预测，可以发现2019年5月至2019年12月全国居民消费价格指数相对保持平稳，并成逐步下降的趋势。