城市轨道交通牵引变电所负荷过程及概率特性研究*
2019-08-19崔洪敏李鲲鹏
崔洪敏 刘 炜 李鲲鹏,2 刘 兰 娄 颖
(1. 西南交通大学电气工程学院,610031,成都;2. 广州地铁设计研究院有限公司,510010,广州;3. 广州地铁集团有限公司,510010,广州//第一作者,硕士研究生)
地铁牵引负荷作为城市轨道交通的一级负荷,所占比例较大。牵引负荷一般具有规律性、流动性、非线性和波动性等特点。因此,有必要对牵引负荷进行研究,掌握其特性,为供电系统设计与电能质量分析提供帮助。
目前,大多数文献针对电气化铁路牵引负荷,建立了其概率模型,在研究新建电气化铁路对电力系统电能质量的影响预测时起到关键作用。文献[1]采用对数正态分布函数来拟合馈线电流的概率密度曲线。文献[2]提出了利用β函数描述馈线电流概率密度的方法,并从形态上进行了对比分析。文献[3]选择带电有效系数、最大值、方差和偏度系数作为描述牵引负荷概率分布的主要特征量。文献[4]建立了高速铁路牵引变电所负荷和负序电流的概率模型。文献[5]为了评估新建电气化铁路对电网电能质量的影响,提出了一种基于实测数据的牵引负荷统计预测方法。文献[6-7]基于牵引运行仿真和牵引供电系统负荷过程进行了仿真研究。
以上文献均是针对电气化铁道馈线电流进行的研究,然而城市轨道交通直流供电电压大多采用DC 750 V/1 500 V供电,电压波动剧烈,因此评估城市轨道交通的牵引负荷过程,不能只考虑馈线电流,应综合考虑牵引网电压和馈线电流。
本文对城市轨道交通的牵引负荷进行了分析,总结得到了负荷过程的一般规律,采用直方图法得到城市轨道交通牵引负荷的分布特征,并通过对牵引负荷进行分类,利用β函数拟合牵引负荷概率密度函数,得出城市轨道交通牵引负荷的概率密度特征,为城市轨道交通牵引负荷过程分析提供了更详尽的信息,有利于掌握城市轨道交通牵引负荷特性,并可用于研究牵引变压器容量占用及过负荷情况,以及指导城市轨道交通供电系统设计和列车安全高效运营。
1 城市轨道交通牵引负荷过程
本文通过对成都地铁、广州地铁、昆明地铁以及上海轨道交通等的典型牵引变电所进行负荷过程测试,累积了众多城市轨道牵引变电所的母线电压与馈线电流负荷过程数据。测试方法为:在城市轨道交通牵引变电所直流牵引网母线加装霍尔电压传感器,在直流进线和直流馈线加装霍尔电流传感器,同步采集直流牵引网母线电压、两路直流进线电流及四路直流馈线电流,可监测城市轨道交通牵引变电所牵引负荷过程。
成都地铁3号线太平园牵引变电所正常供电运行时负荷过程如图1~2所示。
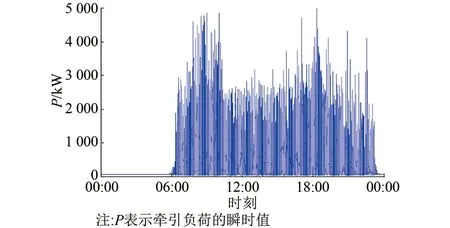
图1 太平园牵引变电所全日牵引负荷曲线

图2 太平园牵引变电所早高峰时段牵引负荷曲线
对成都地铁和广州地铁的相关牵引变电所负荷过程数据进行了统计,如表1和表2所示(其中,广州南和白云文化广场牵引变电所属于广州地铁,其余变电所属于成都地铁)。其中:负荷率计算方法如式(1)所示,其反映了负荷整体波动及冲击水平;负载率计算方法如式(2)所示,其代表实际负荷对整流机组的利用率,反映了整流机组当前供电的可靠性及供电能力水平。
KL=Sa/Sm
(1)
KP=Sa/S
(2)
式中:
KL、KP、Sa、Sm、S——分别代表负荷率、负载率、牵引负荷均值、牵引负荷最大值以及整流机组安装容量。

表1 相关牵引变电所牵引负荷过程均值统计
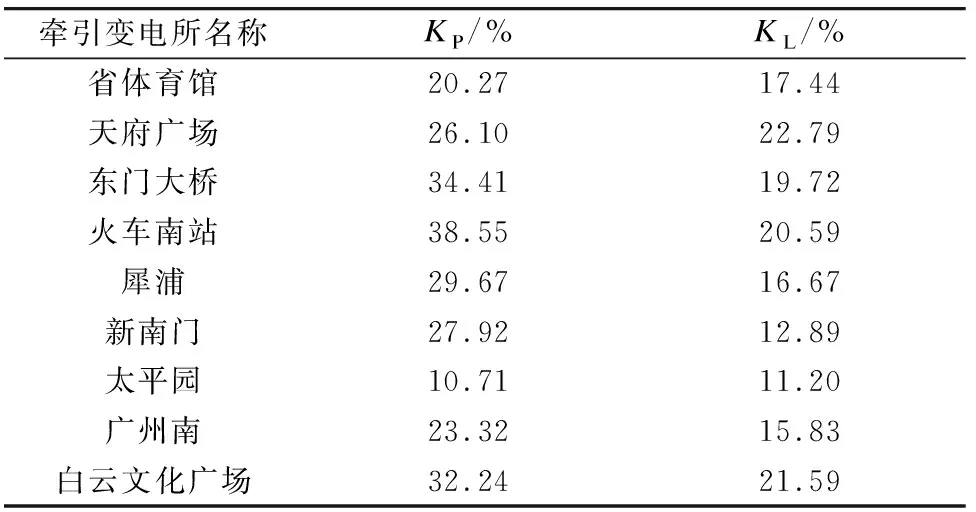
表2 相关牵引变电所早高峰时段负载率与负荷率统计
图1中,城市轨道交通存在非运营时段和运营时段,两个时段牵引负荷过程差异明显,其中,运营时段的列车牵引负荷波动较为剧烈;图2中,早高峰时段牵引负荷呈尖峰分布,存在一定的规律性,这和地铁站间距较短、列车反复起停有关。
由表1可知,高峰时段的牵引负荷均值是全日牵引负荷均值的1.18~2.34倍。由表2可知:牵引负荷为冲击负荷,高峰时段负荷率为11%~23%,峰值功率是平均功率的4.35~9.10倍;轨道交通牵引负荷高峰时段负载率较低,为10%~40%。
2 城市轨道交通牵引负荷分布特征
对城市轨道交通牵引负荷曲线的特性进行分析,有利于掌握轨道交通负荷特征,理解轨道交通牵引负荷的变化规律,指导供电系统设计和运营。通过以上分析可知,城市轨道交通的牵引负荷不具有一般的规律性,因此对个别负荷的分析意义不大。通用的做法是将牵引负荷过程视为随机过程处理,用数理统计的方法来描述其一维分布函数[1]。当样本容量较大并且对其进行合理分组时,直方图以很高的概率接近随机变量的概率密度函数[2]。采样仪器的采样周期为3 s,运营时段的牵引负荷共计约21 600个采样数据,属于大容量数据,因此本文采用直方图法是可行的。
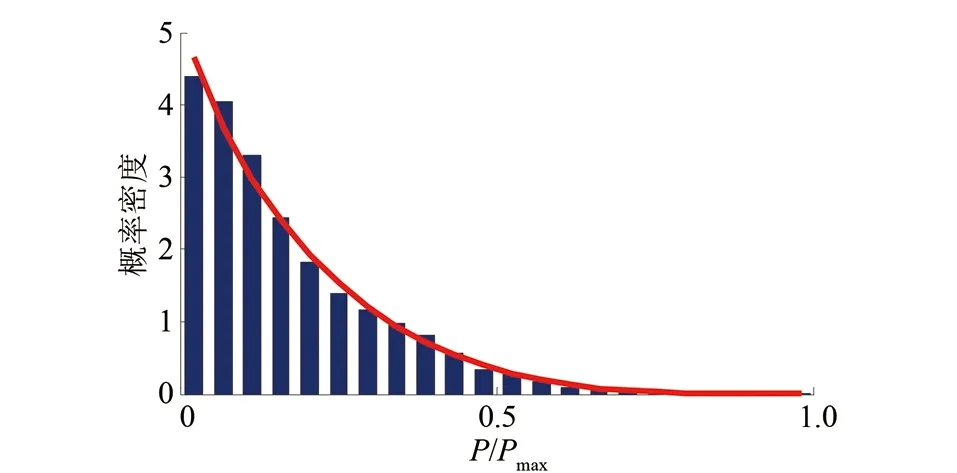
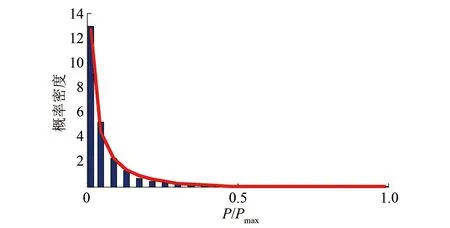
对部分牵引变电所的牵引负荷作出概率密度直方图,为保证面积和为1,纵坐标取nfi(n为负荷分区数目,fi为落在每个负荷区间的频率)。其中,白云文化广场和太平园牵引变电所牵引负荷的概率密度直方图如图3和图4所示。

图3 白云文化广场牵引所牵引负荷概率密度直方图

图4 太平园牵引所牵引负荷概率密度直方图
根据统计得到的直方图,结合概率密度函数的特性,可以得到城市轨道交通牵引变电所牵引负荷概率密度呈左偏单峰分布,概率密度最大值均出现在小负荷区段,概率密度随功率增大而减小,其不具有对称性。
3 城市轨道交通牵引负荷概率密度函数
上文基于大量的实测数据,统计分析了牵引变电所的牵引负荷过程及其分布特征。但是基于统计分析的方法需要得到大量的实测数据,过程较为繁琐。如果在仅提供负荷最大值及均值等少量数据时,可以得到牵引负荷的负荷过程与分布特征,就大大简化了工作。采用已知函数拟合样本的概率密度,只需确定少数几个参数就能确定它的概率密度函数,这为计算机的数值计算提供了很多方便,对掌握负荷的分布特点亦有很大帮助。
文献[8]通过大量实测数据对贝塔分布与正态分布的拟合效果进行比较,得到贝塔分布拟合效果最佳。文献[9]对比了贝塔分布、正态分布与瑞丽分布的拟合效果,选择了拟合效果最好的贝塔分布。本文通过计算贝塔分布对城市轨道交通牵引负荷的拟合误差,验证了运用贝塔分布分析城市轨道交通牵引负荷分布的可行性,并简单介绍了其在城市轨道交通牵引负荷概率密度拟合应用中的原理。
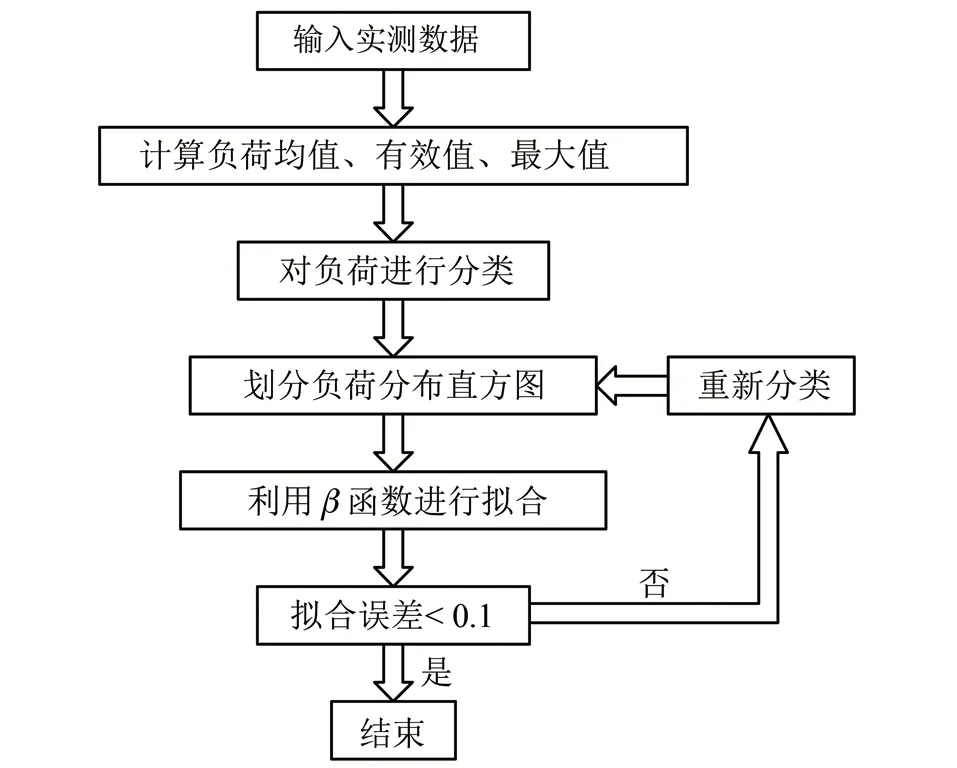
设随机变量X符合β分布记做X~β(a1,a2),其中a1和a2为分布参数。当随机变量a (3) 当0 (4) 设负荷均值为Pm,负荷均方根值为Ps,最大值为Pmax,带电有效系数为K0。地铁采用双边供电,接触网全线贯通,针对地铁运营时间段的牵引负荷进行统计,因此不考虑空载时间段,故K0如式(5)所示。参数a1和a2可以由式(6)~(7)求得,当a1和a2已知时,β分布随之确定。 (5) (6) (7) 为了评估城市轨交通道牵引负荷密度函数的拟合程度,需要计算其拟合误差: (8) 式中: MES——均方差; S——负荷区间中点处直方图的概率大小; f——负荷区间中点处拟合曲线函数。 由于在运营时段内,城市轨道交通牵引负荷波动异常剧烈,因此如何对波动剧烈的负荷进行拟合是亟待解决的问题。通过分析发现,可以将实测牵引负荷的负荷均值以及与最大值接近的牵引负荷视为同一类负荷,因此可以据此方法将牵引负荷分成不同的负荷类型。 城市轨道交通牵引负荷概率密度拟合流程如图5所示,牵引负荷特征值统计如表3所示。不同类型牵引负荷的概率密度拟合曲线如图6~10所示,牵引负荷的分布参数及拟合误差的统计值如表4所示。 图5 牵引负荷概率密度拟合流程图 牵引变电所名称负荷均值/kW负荷有效值/kW负荷最大值/kW白云文化广场1 1071 4636 568火车南站9611 3456 481东大路2654854 644太平园3696625 075新南门1 0741 67810 826 根据前文提到的分类方法,表3中白云文化广场和广州南站牵引变电所的牵引负荷属于同一类负荷,东大路和太平园牵引变电所的牵引负荷属于同一类负荷,新南门牵引变电所的牵引负荷属于另一类负荷。对牵引负荷进行分类,增加了该方法的通用性。 图6 白云文化广场牵引所牵引负荷概率密度拟合曲线 图7 火车南站牵引所牵引负荷概率密度拟合曲线 图8 东大路牵引所牵引负荷概率密度拟合曲线 图9 太平园牵引所牵引负荷概率密度拟合曲线 由图6~10以及表4可知,利用本文提到的负荷分类方法,采用β密度函数对各类牵引负荷的拟合效果较好,拟合误差均在0.1以内,表明本文采用的负荷分类方法以及采用β分布函数拟合城市轨道交通牵引负荷概率密度函数的方法是可行的。 图10 新南门牵引所牵引负荷概率密度拟合曲线 牵引变电所名称K0a1a2拟合误差/%白云文化广场1.322 40.944 74.661 71.64火车南站1.400 50.736 94.235 53.79东大路1.830 60.345 35.702 13.37太平园1.694 90.417 35.000 29.84新南门1.516 70.561 55.093 49.01 本文通过对城市轨道交通牵引负荷的负荷过程与概率特性进行分析,得到以下结论: 1) 正常供电运行时,城市轨道交通高峰时段负荷率大多位于11%~23%,高峰时段的负载率一般位于10%~40%,说明现阶段城市轨道交通牵引负荷具有较大的冲击性,现阶段整流机组利用率较低。 2) 本文通过对牵引负荷进行分类,采用β密度函数对牵引负荷的概率密度函数进行拟合,拟合误差均在0.1以内,表明本文采用的负荷分类方法以及用β密度函数拟合城市轨道交通牵引负荷概率密度函数的方法是可行的。在仅掌握少数负荷参数时,本方法可为城市轨道交通牵引负荷过程分析提供更详尽的信息,有利于掌握城市轨道交通牵引负荷特性,为城市轨道交通牵引变电所的容量设计和安全高效运营提供依据。
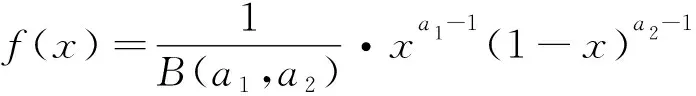


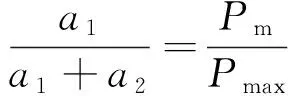







4 结论
