基于CR-NOMA网络的功率分配策略及中断性能分析

2019-08-19郭道省李明贵

网络安全与数据管理 2019年8期

李成，郭道省，李明贵

(1.陆军工程大学通信工程学院，江苏南京 210001；2.63780部队，海南陵水 572427)

0 引言

非正交多址接入(Non-orthogonal Multiple Access，NOMA)通过引入功率域复用，允许多用户共享时频资源，从而可以提高频谱效率并增大网络接入点密度，是未来无线通信的关键多址接入技术[1]。NOMA通过采用功率复用技术给不同用户的信号分配不同的功率，并在发射机处进行叠加编码。接收机采用串行干扰消除(Successive Interference Cancellation，SIC)实现多用户信号的检测[2]。另一种可以改善频谱效率的技术是认知无线电(Cognitive Radio，CR)。特别地，本文考虑的是底层认知无线电(Underlay Cognitive Radio)场景，即在保证主用户的服务质量(Quality of Service，QoS)的情况下，允许次级用户访问主网络的频谱[3]。可以预见，将NOMA和CR这两种技术相结合可以显著提高系统性能,即CR-NOMA。

NOMA系统的功率分配问题已经得到了广泛的关注和研究。文献[4]研究了基于比例公平的用户配对及功率分配方案，以确保小区边缘用户的公平性。文献[5]针对NOMA中继网络，提出了一种能够最小化系统中断概率同时能够保证传输速率的功率分配方案。文献[6]考虑了NOMA网络下行链路蜂窝系统，结果表明功率分配因子的选取对系统的中断性能有着重要的影响，并且与OMA(Orthogonal Multiple Access)相比，NOMA能够获得更大的遍历容量。文献[7]研究了underlay CR-NOMA协作网络的中断性能，其中，考虑了非理想SIC对系统性能的影响。文献[8]基于相同的模型，研究了非理想信道状态信息对译码的影响，同时比较了NOMA网络和OMA网络的中断性能。

本文针对下行链路underlay CR-NOMA中继网络进行研究。网络模型考虑了主网络对次级网络的干扰以及主网络的干扰温度约束(Interference Temperature Constraint,ITC)。从中断概率的角度出发，研究了功率分配问题，并分析了功率分配因子对系统中断性能的影响。

1 系统模型

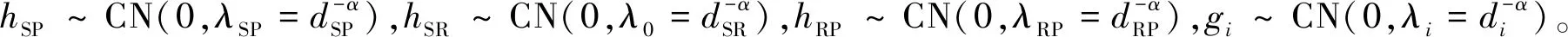
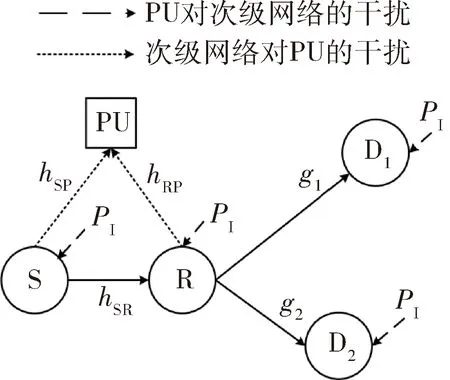
图1 下行链路CR-NOMA中继网络

对于underlay CR场景，为了确保主网络能够可靠通信，源端S的发送功率要受到限制[9]：

(1)

(2)

其中，I表示PU处的干扰温度约束，P和βP分别表示源端S和中继R的最大平均发送功率。

一个完整的通信过程包含两个阶段。第一阶段，S发送叠加编码信号给中继R，R收到的信息为：

(3)

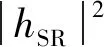
(4)

(5)

(6)

则D1译码x1时的SINR为：

(7)

D2译码x1和x2时的SINR分别为：

(8)

(9)

随机变量X的积累分布函数(Cumulative Distribution Function，CDF)为：

ε,ρ>θ)

(10)

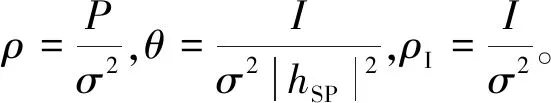
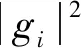
(11)

2 中断概率及功率分配方案

2.1 中断概率

接收端成功译码xi需要满足γ(·),i>εi=22ui-1，其中ui表示译码消息xi所要求的目标速率。因此，用户D1的中断概率可定义为：

=1-P(X>φ1,Y1>ξ3)

=1-[1-FX(φ1)]·[1-FY1(ξ3)]

(12)

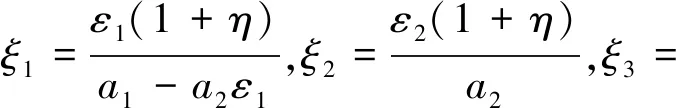
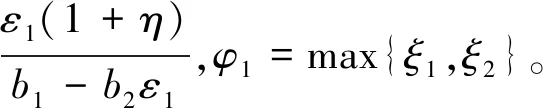
a2ε1且b1>b2ε1，否则，中断概率为1。

将式(10)、(11)代入式(12)中，可得：

(13)

同理，用户D2的中断概率为：

=1-[1-FX(φ1)]·[1-FY2(φ2)]

(14)

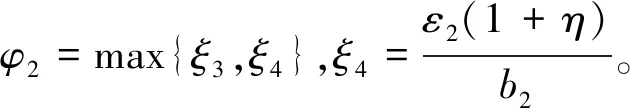
整个系统的中断概率为：

Pout=1-P(γR,1>ε1,γR,2>ε2,γD1,1>ε1，γD2,1>ε1，γD2,2>ε2)

=1-[1-FX(φ1)]·[1-FY1(ξ3)]·[1-FY2(φ2)]

(15)

2.2 功率分配方案

本小节以最小化系统中断概率为目标，研究功率分配方案，确定最佳的功率分配因子。优化问题如下：

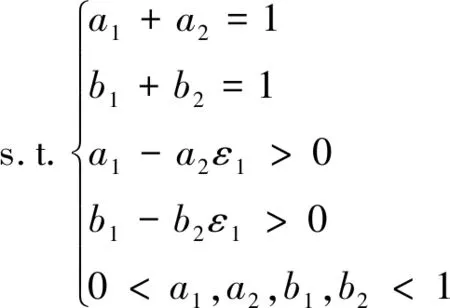
(16)

上述问题可以转化为式(17)和式(19)两个子问题分别进行优化。子问题1为：

=minmax{ξ1,ξ2}

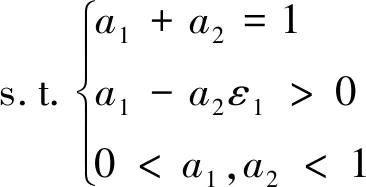
(17)

上述问题为凸规划问题，当ξ1=ξ2时取得最优解[10]，此时源端的功率分配因子为：

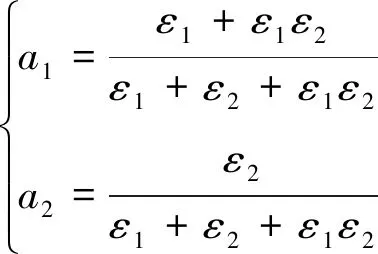
(18)

子问题2为：

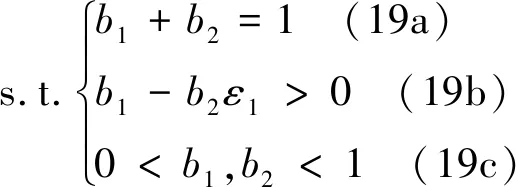
(19)

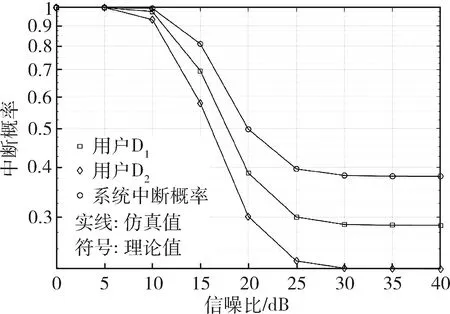
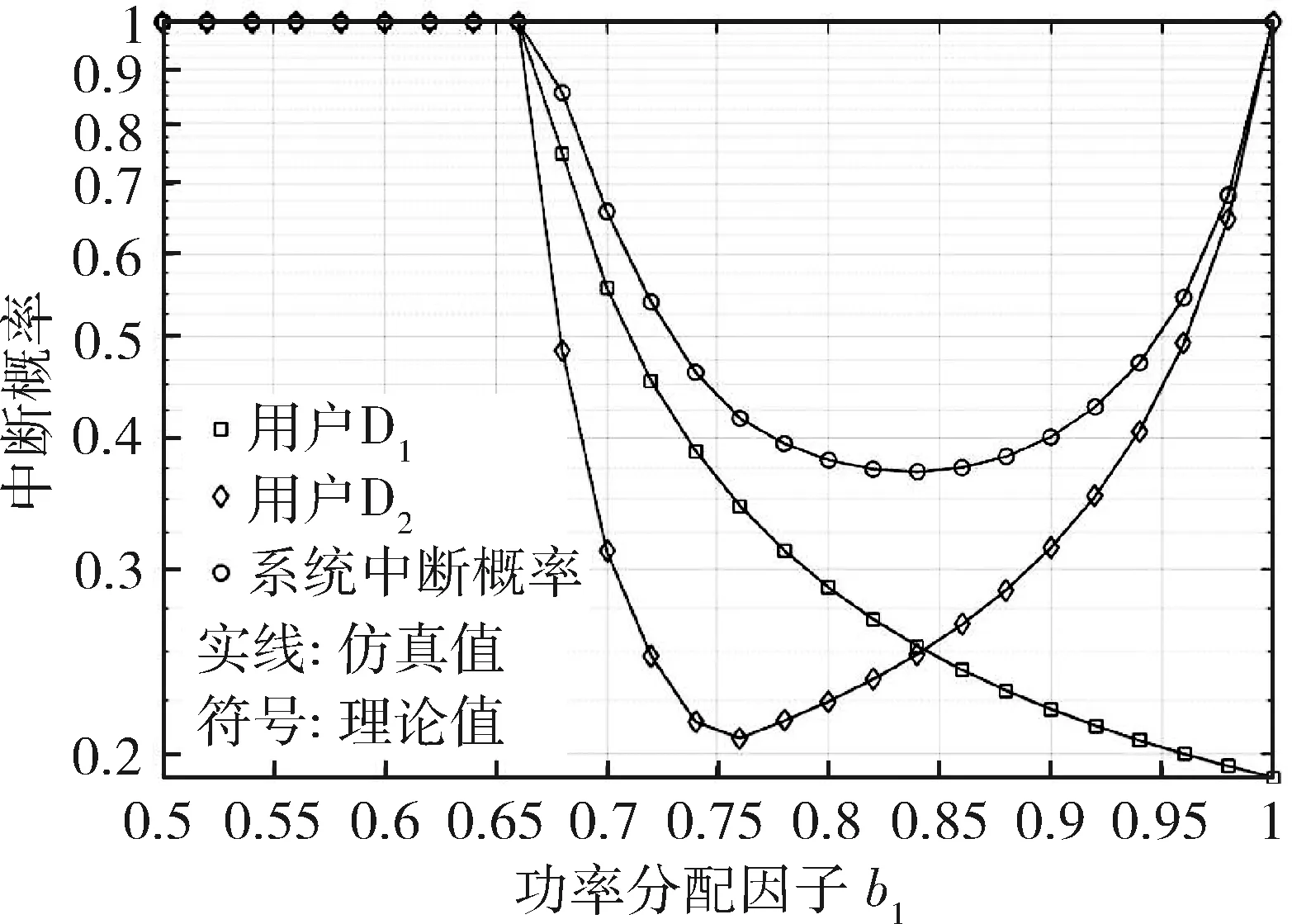
公式(19b)要求ε1/(1+ε1)

3 仿真结果分析

本节通过MATLAB仿真分析系统的中断性能。系统参数设置为：dSP=dRP=d0=d2=1，d1=1.5d2，α=3，β=1，σ2=1，η=0.5，b1=0.8，b2=0.2，ε1=ε2=3 dB[8]。另外，a1和a2的取值由公式(18)确定。理论值是通过公式算出来的精确解，即根据统计信道状态信息来计算结果。仿真值是通过蒙特卡洛仿真计算出来的基于信道随机性的统计平均值，蒙特卡洛仿真次数为106。

图2为系统及用户中断概率随信噪比变化示意图，并规定I=20 dB。从图中可以看出，中断概率随着信噪比的增加而降低，并最终趋近于一个定值，出现“中断平台”效应。这是因为在认知场景下，源端的发送功率是受限的。从图中还可得知，用户D2的中断概率低于用户D1的中断概率，这是因为用户D1距离中继更远，由于信道衰落，译码时的SINR值较低。