500kV单回路复合横担塔塔线体系动力响应分析∗
2019-08-19田宇孙清李西瑞赵雪灵王志强
田宇 孙清 李西瑞 赵雪灵 王志强
(1.中国能源建设集团山西省电力勘测设计院有限公司 太原030001; 2.西安交通大学 710049;3.电力规划总院有限公司 北京100120)
引言
复合横担杆塔又称复合塔,是目前电力线路上常采用的以复合材料横担代替传统钢制横担的新型杆塔形式。复合横担杆塔用于输电线路有着节约钢材、减小塔头尺寸、减少走廊宽度的特点; 并且由于复合横担与传统钢制横担相比更为轻便与易加工成型,可以大幅度地降低杆塔的运输和组装成本; 杆塔的耐腐蚀、耐高低温、强度大、被盗可能性小的特点又可以降低线路的维护成本[1]; 同时,复合杆塔利用复合材料的绝缘特性,可实现结构材料和功能材料的高度统一,具有许多显著的优势。其中最主要的优势便是复合材料良好的绝缘性能使得其能够替代绝缘子,从而大幅度减小了悬垂串长度,降低塔高[2,3]。
输电线覆冰是指空气中的水分或降雨因冻结而成冰霜的一种自然现象。在特定的温度和风等自然条件下,输电线覆冰脱落会引起电线的上下振动和横向摆动,工程中亦称“冰跳”。覆冰脱落后,导线内积聚的势能得到释放,迅速向上跳起,并使相邻档之间产生纵向不平衡张力,输电线的跳跃会减少线路之间的安全距离,造成闪络或短路,同时可能会导致线路断线断股,杆件破坏甚至倒塔等工程事故的发生。断线是输电塔纵向不平衡荷载由来之一,断线事故虽然是小概率事件,但是一旦发生,不仅损坏电气设备,还会引起整个输电系统的振荡,使输电塔的位移、内力响应加大,甚至导致输电塔倒塌,使整条线路瘫痪以及产生火灾等灾害。由此可见,根据输电线路的实际情况,进行覆冰脱落以及断线的动力分析是十分必要的[4]。
本文通过有限元仿真分析,建立500kV单回路复合横担塔有限元梁杆模型,及3 塔4 线的塔线耦合体系模型,并对3 塔4 线模型进行塔线体系的覆冰脱落及断线工况下的动力响应分析,以检验该塔型结构的合理性与可靠性。
1 单塔有限元模型
杆塔设计参数见表1。

表1 杆塔设计参数Tab.1 Design parameters of tower
杆塔塔身主要由角钢组成,其中主材多为Q420 钢与Q345 钢,斜材多为Q345 钢与Q235钢,辅助材多为Q235 钢。横担采用复合材料,具体材料参数见表2。

表2 梁杆模型主要构件材料参数Tab.2 Material parameters of main components
建立如图1 所示的单塔有限元模型。

图1 单塔梁杆有限元模型Fig.1 Finite element model of single tower
2 塔线耦合体系模型建立
输电塔-线体系是由塔身构件和导线两种不同性质的材料组合而成,两者相互协调、相互影响,塔线体系是一种大位移空间体系,非线性因素很强。为研究塔线体系脱冰、断线等动力响应,首先需要建立输电塔-线体系有限元模型。
2.1 导地线模型
考虑输电线的非线性,可将导线处理成单索结构,单索结构的特点是理想柔性,它既不能受压也不能抗弯,而且材料符合胡克定律。有限元方法将索看成一系列相互连接的索段,索段之间以节点相连。若索受沿索弧长均布荷载q(如自重),其初始状态解为—族悬链线:


设跨中垂度为f,则当x=l/2 时,y=f,则:

由推导可知,索的垂度和水平张力互为结果,即索的线形为一悬链线族,若已知其中某一个参数即可唯一确定所得线形和张力[5]。
表3 为输电线主要参数。

表3 导、地线主要参数Tab.3 Main parameters of guide and ground wire
将表3 中的单位长度重量和水平张力代入公式计算分别得到导线和地线的悬链线方程便可得到输电导地线在自重作用下的形状。采用杆单元LINK10 进行建模,它是一种带预应力的直线单元,承受轴向拉力。在单元的每个节点上有三个自由度: 沿X、Y和Z三个方向的平动,可模拟几何大变形[6]。
2.2 绝缘子串模型
绝缘子串的几何模型如图2 所示,其中串子杆采用LINK 单元,其余部分即串子梁部分采用BEAM 单元进行模拟,建模具体参数如表4 所示。

图2 绝缘子串模型Fig.2 Insulator s model

表4 绝缘子串主要参数Tab.4 Main parameters of insulator string
2.3 塔线体系模型
输电导线采用的是4×JL/G1A-400/35 型号导线,地线采用JLB20A-150 型号线,有限元模型采用实际的四分裂导线通过绝缘子串和输电塔连接,输电塔水平向设计档距500m。输电塔底部和输电线端部均采用固接约束。塔线的体系模型如图3 所示。
3 塔线体系断线动力分析
本文对高压输电塔-线体系的断线模拟计算过程采用以下3 个步骤:
(1)对输电塔-线体系进行静力分析,得到输电线的张力;
(2)去掉断线档输电线最外端的约束,通过施加等效荷载F进行等效;
(3)定义时程力F,假定前0.01s 为输电线的张力,通过突然卸载的方式模拟断线对输电塔的冲击作用[7,8]。

图3 塔线体系模型Fig.3 The model of tower-line system
断线计算工况如表5 所示,断线档均取为第三档。
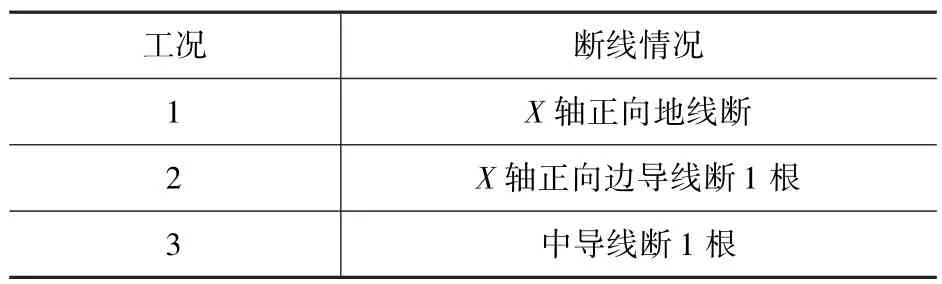
表5 断线计算工况Tab.5 The conditions of bolting
3.1 导线时程响应
图4、图5 绘出了边导线断线工况下的导线响应,由于篇幅限制其余工况计算结果汇总于表6、表7。
所有工况中导线、地线在断线后断线档导地线均存在反弹现象,其中中导线断线后断线档其余导线反弹值最大可达6.6m。地线断线后,最大张力出现在其邻跨地线,最大张力变化幅度为15%。而导线断线后,最大张力出现在断线档其余导线,其中中导线断线工况中断线后其余三根导线张力变化幅度最大可达36%。规范规定的“弧垂最低点最大张力不超过其导、地线拉断力的70%”。经过计算,导地线拉断力的70%分别为118.75kN 与68.94kN。断线工况下线内跨中最大张力满足《110kV ~750kV 架空输电线路设计规范》(GB 50545 -2010)[9]要求。

图4 各档导线跨中竖向位移时程Fig.4 Vertical displacement s time history of wire
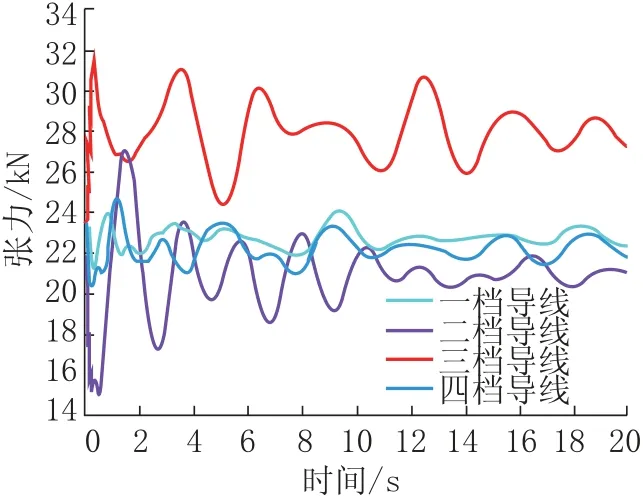
图5 各档导线张力时程Fig.5 Tension s time history of wire

表6 导线跨中竖向位移响应最大值Tab.6 Maximum of vertical displacement response

表7 导地线张力最大值Tab.7 Maximum of the tension
3.2 整塔时程响应
边导线断线工况下的三塔塔头位移时程如图6所示,其余工况下的塔头响应列于表8。

图6 塔头位移时程Fig.6 Time history of tower s displacement
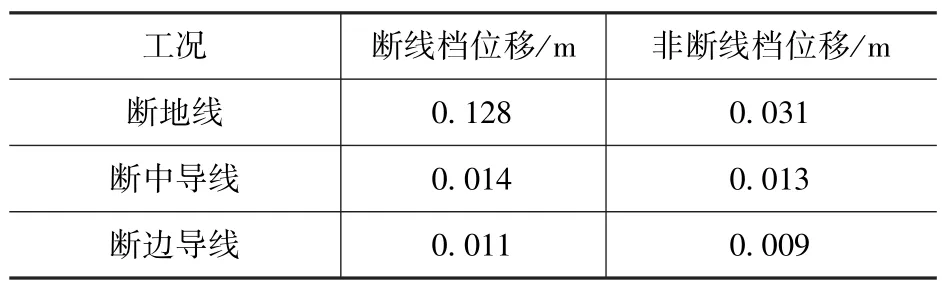
表8 塔头位移最大值Tab.8 Maximum of tower s displacement
从图6 可以看到,断线后前2s 整塔响应剧烈,之后塔头位移变化呈现出一定周期性且变化幅值趋于稳定,与断线档直接相连的整塔响应大于远离断线档整塔。
从表8 可以看到,断线工况对塔头位移影响较大的为断地线工况,与断线档直接相连的塔头位移最大值可达0.128m,而远离断线档塔头位移影响不大。另外,中导线与边导线断线对塔头位移的影响也较小。
3.3 横担时程响应
此处以中横担分析结果为例。由于断地线与断边导线工况对中横担的轴力影响较小,对此两种工况进行边横担轴力的时程分析意义不大,故此处仅对断中导线这一工况进行分析。

表9 横担位移分析结果Tab.9 Results of the cross-arm s displacement
可以看到,中导线断线后横担响应对于与之相近的2,3 塔和远离断线档的1 塔而言区别不大。横担位移的影响均在0.01m 左右,为整塔计算高度的0.18H/1000(其中H为整塔高度),符合规范3H/1000 的限值规定,说明中横担上下杆材刚度较充足。
3.4 绝缘子时程响应
表10、表11 列出了三个断线工况下的中、边导线的绝缘子轴力最大值。图7 为中导线断线工况下的绝缘子轴力时程。

表10 中导线绝缘子轴力(单位: kN)Tab.10 Axial force of medium phase insulator(unit: kN)

表11 边导线绝缘子轴力(单位: kN)Tab.11 Axial force of edge phase insulator (unit: kN)
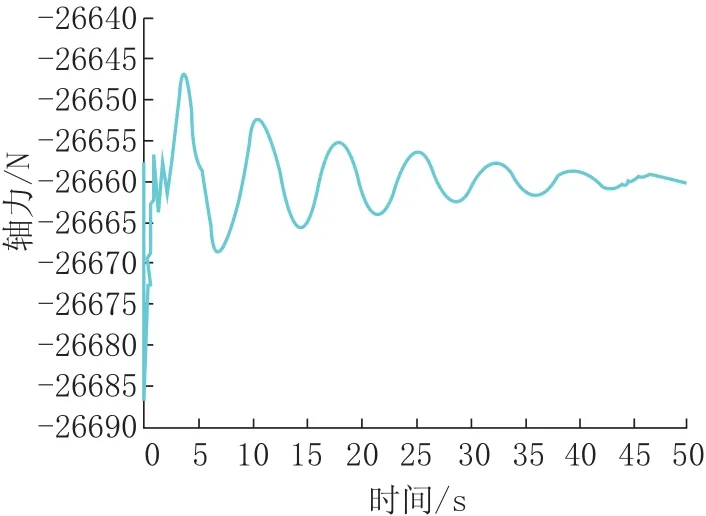
图7 中导线绝缘子轴力时程Fig.7 Time history of insulator s Axial force
可以看到静力状态下绝缘子串子杆轴力为26.66kN,不论是边导线或是中导线的绝缘子,地线断线对绝缘子轴力几乎无影响。边导线断线使边导线绝缘子轴力增至38.22kN,中导线断线使中导线绝缘子轴力增至35.28kN。
4 塔线体系覆冰脱落动力分析
实际的覆冰断面可能是各种不规则的形状,但在输电线路设计中覆冰截面通常按等厚中空圆形考虑。本输电线路覆冰厚度10mm,覆冰密度为0.9g/cm3,导线换算冰荷载为4.13N/m,地线换算冰荷载为3.16N/m。覆冰脱落分析中不考虑风力、温度等影响。通过对输电线有限元模型施加节点力的方式模拟均布冰荷载[10,11]。
对于导线脱冰的模拟,采取以下步骤:
(1)计算塔线在自重作用下平衡状态;
(2)计算导线在10mm 均匀覆冰作用下的塔线体系平衡状态;
(3)使某一跨(根)导线的覆冰在很短时间内突然脱落;
(4)得到覆冰脱落后塔线体系的响应。
对于“三塔四线”输电塔线体系,覆冰脱落的情况多种多样,这里只选取典型的三个工况进行瞬态动力分析,三个典型工况均为第三档脱冰,如表12 所示。其中参考《中重冰区架空输电线路设计技术规定》(Q/GDV182 -2008),定为80%脱冰量脱冰[12]。

表12 覆冰脱落计算工况Tab.12 The conditions ofice shedding
4.1 导地线分析结果
列出三个覆冰脱落工况下四档导线跨中竖向位移最大值于表13,图8 绘出中、边导线覆冰脱落后各档导线的竖向位移时程。

表13 跨中导地线位移最大值Tab.13 Maximum displacement of lines
从图8 中可以看到,中导线与边导线均是在第三档导线覆冰脱落后3s 位移达到最大值4.5m,而后在阻尼作用下缓慢衰减。并且通过对比可以看出,第三档导线脱冰后向上跳跃,其位置最终稳定在全跨覆冰时导线位置的上部,而第一、第二及第四档导线则稳定在全跨覆冰时导线位置的下部。对于导线的响应,本跨导线最大,邻跨次之,隔跨最小。
图9 绘出中、边导线覆冰脱落后各档导线的张力时程(第三档脱冰工况下,邻跨的第二和第四档张力变化值非常接近,此处仅绘出第一档、第二档和第三档的张力变化)。第三档脱冰时三个工况下的中导线脱冰张力变化值见表14。
可以看到,覆冰前导线张力为23.45kN,覆冰后线内张力32.21kN,增长幅度为37%。而经过脱冰过程,导地线内张力得到一定程度的释放与平均,最终趋于稳定,张力释放约12%,四根导线张力变化较为均匀。表15 验算“弧垂最低点最大张力不超过其导、地线拉断力的70%”,覆冰工况下线内跨中最大动张力满足要求。

图8 导线脱冰跨中位移时程Fig.8 Time history of line stripping

图9 导线张力时程Fig.9 Time history of the line s tension

表14 中导线脱冰张力变化值Tab.14 Tension variation of line stripping

表15 中导线张力验算Tab.15 Checking of the tension of lines
4.2 横担分析结果
绘出中、边横担压杆轴力时程如图10 所示。由图可知,第三档脱冰对靠近脱冰档的塔2 与塔3 影响更大。
对于边横担,全跨覆冰时塔3 的两横担两压杆均承受约8.5kN 的压力,塔2 脱冰档侧横担在3.2s 时承受的压力达到峰值15kN,塔3 靠近脱冰档侧横担在3.3s 时承受的压力达到峰值14kN。

图10 横担压杆轴力时程Fig.10 Time history of arm s axial force
全跨覆冰时塔3 的两横担两压杆均承受约5kN 的压力,塔2 脱冰档侧横担在3.2s 时承受的压力达到峰值8.5kN,塔3 靠近脱冰档侧横担在3.3s 时承受的压力达到峰值9kN。
4.3 绝缘子分析结果
表16 列出了三个覆冰脱落工况下的中、边导线的绝缘子轴力值。可以看到,在脱冰后的“冰跳”过程中绝缘子杆轴力未超过覆冰静轴力。
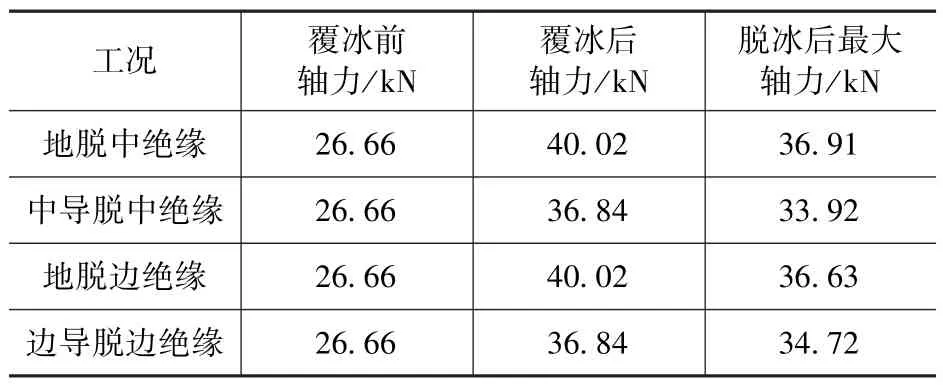
表16 绝缘杆轴力Tab.16 Axial force of insulators
4.4 整塔分析结果
表17 列出了与各工况下三基塔有冰与脱冰两侧塔头X向位移的最大值。图11 绘出了边导线覆冰工况下各塔塔头的位移时程。

表17 塔头位移Tab.17 Tower s displacement
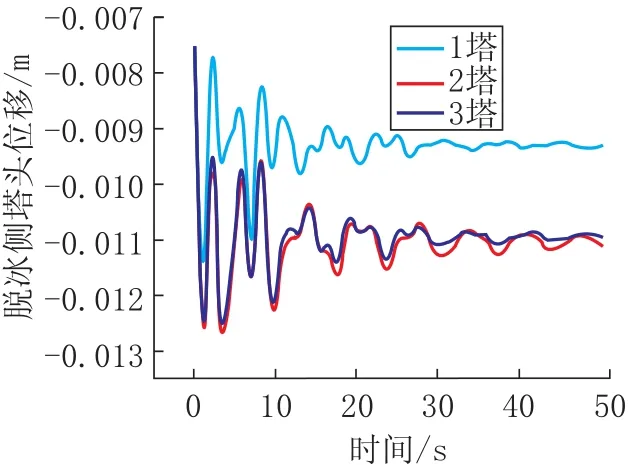
图11 边导线脱冰塔头位移Fig.11 Tower s displacement of sideward detachment
通过提取各塔塔头位移时程来研究导线脱冰对输电塔的整体冲击。可以看到,各工况下塔头位移最大值不超过0.02m。导线脱冰后2 塔与3塔塔头位移响应明显大于远离脱冰档的1 塔,最大位移出现在脱冰后2.1s,最大值为0.013m。可见覆冰脱落对整塔冲击的影响普遍较小。
5 结论
本文建立了500kV 单回路复合横担直线塔的有限元梁杆模型及3 塔4 线塔线体系模型,通过动力时程模拟得出500kV 单回路三相复合横担直线塔在断线工况与覆冰工况下的动力响应,分析整塔各部件响应的变化情况,主要得出以下结论:
1.断线与覆冰的动力工况下本档导线在冲击作用下均会产生垂直导线方向反弹,并且最终稳定与平衡位置上方。导地线内张力在动力过程中最高可提升30% ~40%,但仍远小于断线张力的70%,安全储备能够满足工程需要。
2.断线工况下横担位移最大值为0.0141m,符合规范3H/1000 的限值规定,横担杆材与管材刚度较为充足。
3.绝缘子串子杆轴力在断线与覆冰工况下提升明显,提升幅度最大可达50%。在绝缘子设计中,串子杆受力性能应当得到保证。
4.各动力工况下的整塔响应均保持在较小水平,断地线工况下塔头位移达到最大值0.12m,塔身刚度储备足够。
