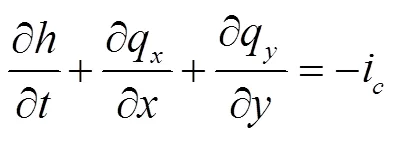欧拉法融合拉格朗日法高效模拟灌溉二维地表水运动规律

2019-08-19章少辉白美健李益农

农业工程学报 2019年12期

史源，章少辉，白美健，李益农

史源，章少辉※，白美健，李益农

（中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100038）

大规模现代化农业灌溉管理下，为实现快速高效地获知灌溉水运动及其分布的目的，该文基于二维浅水方程组的欧拉-拉格朗日混合型表达形式，提出了一种高效简洁的欧拉-拉格朗日混合解法。该解法的基本物理变量被严格地定义在欧拉型非结构化三角形有限体积单元格上，且变量在单元格之间呈现出阶梯分布状态，以精准地捕捉各类地表浅水波动并有效地保持质量守恒性；由于控制方程中不存在水运动的对流梯度项（或位置加速度项），仅通过拉格朗日迹线追踪的形式获得未知与已知时间步之间的变量关系，故与广泛应用的欧拉解法相比，离散格式表达式极为简洁易用；在地表水运动的干湿边界处，地表水位梯度项被做了修正，以严格地保证各物理量之间的数值平衡，进而能高精度的模拟整个畦田内的地表水流推进/消退全过程。为验证模型的模拟性能，选取一种高效的欧拉解法（非迭代型全隐式标量耗散有限体积法）求解二维浅水方程组做为对比模型，基于3个典型畦灌试验的实测数据，从模拟精度、质量守恒性和计算效率3个方面，对比分析了2种数值解法的性能。结果表明，2种解法在模拟精度方面相差无几，且欧拉-拉格朗日混合解法比欧拉解法具有更好的质量守恒性；在计算效率方面，欧拉-拉格朗日混合解法比欧拉解法的效率提高了约5.3倍。故该文提出的二维浅水方程组的欧拉-拉格朗日混合解法，更适用于二维灌溉地表水运动的模拟分析。

灌溉；非线性方程；数值分析；欧拉解法；拉格朗日解法；二维；浅水方程组

0 引言

地面灌溉在中国农业灌溉中应用极为广泛[1-2]。采用数值模拟方法开展灌溉条件下地表水运动模拟与分析，是提高灌溉系统性能的重要手段[3-4]。在大规模集约化农业种植下，地面灌溉往往呈现出典型的二维特征，此时通常采用二维零惯量方程组或二维地表浅水（或全水动力学）方程组描述灌溉地表水流运动过程[5-12]。零惯量方程组忽略了非线性极强的对流梯度项（或位置加速度项），故易求解，但在复杂地形变化情景下，会出现不可预测的误差、并增大了参数的敏感性[13-14]。故近年来，随着计算技术与数值分析的发展，多采用完整的二维浅水方程组描述灌溉地表水运动过程[4]。

针对二维地表浅水方程组，学者们多采用针对Riemann问题的显式Roe算子有限体积法求解[10-12]。但该解法稳定性限制极为严格，且空间离散格式复杂而不易掌握，故出现了混合数值解法[15-17]。相对于显式Roe算子有限体积法，混合数值解法虽然提高了时空离散步长的取值范围，但仍属于有条件稳定。为此，（迭代或非迭代型）全隐式标量耗散型有限体积法应运而生[4,17-19]，具有无条件稳定的显著特征，使得时间步长可依据具体的实例选取，应用更具灵活性。这些已有解法都属于欧拉解法范畴。地表浅水方程组中对流梯度项（或位置加速度项）的存在导致了极为复杂的非线性特征[20-21]，无论如何构造和发展数值解法，欧拉解法都无法绕开这个非线性极强的对流梯度项[22-25]，这使得任何欧拉解法的空间离散格式都比较复杂，而不易被使用者掌握。

求解地表浅水方程组的另一类解法属于拉格朗日解法范畴[25]。最著名的拉格朗日算法当属光滑粒子流体动力学解法（smoothed particle hydrodynamics，SPH）[26-27]，其优点在于通过引入水流轨迹追踪来消除非线性极强的对流梯度项，故空间离散格式简洁易懂，且极易模拟出强非线性的波浪激溅等大变形水运动过程，这是欧拉空间区域，且需考虑粒子之间的相互作用，故初始与边界条件难以设置，效率亦比欧拉法显著降低，粒子之间不确定的相互作用也导致拉格朗日解法具有更严格的稳定性条件。另一种常见的拉格朗日解法被称作粒子-单元格解法（particle-in-cell，PIC）[28]，在该解法中，由于任意空间单元格中的粒子数会随时间变化，同样存在着SPH类似的问题[29]。

综上，欧拉解法具备优良的物理守恒性，但数学结构复杂导致不易被掌握和应用，这源于其非线性极强的对流梯度项。而拉格朗日解法以其独特的轨迹追踪优势有效地消去了该项，但海量空间粒子的引入大大降低了计算效率、增大了初始与边界条件设置的难度。为此，本文针对地面灌溉水流问题，综合欧拉和拉格朗日解法之优势，提出欧拉-拉格朗日混合解法，在保持精度的条件下实现高效快速地模拟分析二维地面灌溉水运动及其分布的目的，并选用一种高效的欧拉解法（非迭代型全隐式标量耗散型有限体积法）做为对比算法，借助3个典型畦灌试验实测结果，从模拟精度、质量守恒性和计算效率3个方面，对比分析该欧拉-拉格朗日型混合解法的模拟性能。