溶质运移中多孔介质弥散度影响因素的SPH模拟研究

2019-08-17饶登宇

水利学报 2019年7期

饶登宇，白冰

（北京交通大学土木建筑工程学院，北京 100044）

1 研究背景

流体在多孔介质中流动的现象广泛存在于工业制造、能源开发、农业生产、环境治理等各个方面［1］。认识多孔介质渗流的溶质迁移扩散规律，将为水土污染治理、垃圾填埋场污染评估、核废料处置库的安全性评估等环境岩土工程问题，提供新的理论依据和解决办法。如果能够在孔隙尺度下从物理本质出发模拟多孔介质中溶质的运移弥散过程，有助于理解弥散现象产生的物理机制，厘清多孔介质弥散度的影响因素。

溶质在土体中的迁移主要包括对流和水动力弥散两个过程［1］。溶质随平均流速运移的过程称为对流运移；水动力弥散包括分子热运动引起的分子扩散，以及由于多孔介质中流体非均匀运动而产生的机械弥散，机械弥散效果与弥散度和流速相关。机械弥散现象的出现从微观尺度上可归结为：（1）同一孔隙内，地下水质点实际流速不等于平均流速u；（2）不同孔隙中孔径不同，地下水质点的实际流速不同，因而不同孔道内的流体质点出现速度差；（3）在直线距离相同时，多孔介质中有的流体质点会比其他质点沿着更长的路径运动。若不考虑弥散度的尺寸效应，则影响机械弥散的两个主要因素可概括为流体质点的速度差以及迂曲路径差。本文将就这两种因素对弥散的影响展开研究。

受限于实验尺度和孔隙结构的复杂性，对于孔隙介质的溶质迁移问题，传统的研究方法一般在表征体元（REV）尺度下采用平均化的状态方程加以概括，认为流体在整个多孔介质的空间内渗流，并不关注孔隙内的实际流动情况，对溶质弥散现象的描述停留在扩散系数、平均流速等若干宏观参数［2］。近年来，孔隙尺度下溶质运移的相关研究有了新的思路：一方面，一些无损测量技术（如计算机断层扫描（CT）技术，X 射线微观成像等）可直观得到多孔介质中的电导率、渗透率以及其他微观结构特征，已经逐步被用于流体在多孔介质内的分布、流动、扩散等研究中［3-4］；另一方面各种新型计算流体力学方法（如SPH（光滑粒子流体动力学）、LBM（格子玻尔兹曼方法）等）不断发展成熟，使得采用数值方法从细观尺度下研究渗流问题成为了可能。数值方法与实验法相比，具有周期短、耗费小且不易受外界环境干扰等优势；与解析法相比，它既可以求解复杂微分方程，又可进行机理研究，并对理论模型进行精确验证。

本文采用的SPH 方法是一种拉格朗日形式的无网格粒子算法，最初被提出是用于解决天体物理学问题，现已被广泛地应用于流体力学。Monaghan［5］将其首先延伸至水动力学的模拟，后续学者进一步采用SPH 方法计算溃坝、水下爆炸、流体与建筑物的相互作用以及孔隙流等问题［6-7］。Morris［8］模拟了低雷诺数下的不可压缩流，并将SPH 方法的计算结果与有限元法进行了对比； Zhu［9］建立孔隙尺度下周期多孔介质渗流计算的SPH 模型，用于求解泰勒弥散问题。Tartakovsky［10］提出多相流模型，拓展了SPH 法在多孔介质和断裂介质中模拟多相流和反应性迁移的应用。Ryan［11］基于SPH 方法建立界面反应模型，模拟溶质的竞争吸附问题，并将孔隙尺度下的模拟结果与达西尺度模型进行对比验证。另一种可用于介观尺度流体力学研究的LBM 方法也受到较多关注。Yang［12］基于LBM 方法模拟讨论了多孔结构随机性、粒径分布和颗粒形状对渗透率的影响，但并未探究多孔结构特性对溶质运移及弥散度的影响。需要指出的是，LBM 方法仍然基于网格，在多尺度问题中，如果计算区域复杂（如大畸变、存在物质交界面或自由表面等）易产生网格扭曲等问题［2］，从而导致数值误差过大或计算不收敛。在处理动量驱动流及多孔介质等复杂几何图形时，SPH 比基于网格的方法有天然优势。首先，线性动量守恒方程的SPH 离散化格式满足伽利略不变性［11］；其次，SPH 的拉格朗日框架能够便捷生成可移动和变形的边界，而不需要复杂的跟踪算法；并且允许在界面上实现复杂的化学或物理作用，比如扩散和吸附作用。

本文基于SPH 方法，从描述流体质点运动和溶质扩散的物理本质出发，在孔隙尺度模拟多孔介质中溶质运移的弥散现象，分析流体质点的速度差和迂曲路径差对机械弥散效应的影响，并讨论弥散度与多孔介质结构参数的关系。

2 SPH 方法基本原理

在SPH 方法中，问题域的状态用一系列粒子来描述，粒子之间不需要任何连接，粒子兼具近似点和材料成分的功能。利用SPH 求解，首先需用积分表示法来近似场函数（场函数核近似法），然后将其离散为级数求和的形式（粒子近似法），则f（x）的积分表达式可写成［10，13］：

式中：W (x-x′，h)为光滑函数，或称核函数，形态如图1中所示，积分表达式中的核函数项可理解为点x′处的函数值在x 处的权重，h 为核函数的光滑长度；Ω为积分区域。图1中κh 为核函数的影响域半径。

将式（1）转化为支持域内所有粒子叠加求和的离散化形式，则第i 粒子点对应的粒子近似式为［13-14］：

图1 粒子近似图

式中：xi和xj分别为粒子点i 和j 对应的坐标，粒子间距xij=xi-xj；相应的mj和ρj为粒子点的质量和密度；以下将W (xij，h)简写为Wij。

本文的核函数选用一种常见的三次B-样条函数［6］：

3 SPH 水动力扩散模型

3.1 质量方程对密度直接使用SPH 近似法，粒子i 密度可通过其支持域内所有粒子的密度加权平均近似得到［6，8］：

式中：n 为粒子i 的支持域内粒子总数；mj为粒子的质量；Wij为粒子j 对粒子i 产生影响的光滑函数。

Randles［15］对式（4）进行了标准化改进：

式（5）的改进可以提高自由边界处和相同材料粒子密度不连续交界面处的精度。

3.2 动量方程对流体微元，动量方程（不考虑重力）可写为：

式中：u 为流速；等式右边两项分别表示单位质量上的各向同性压力差产生的力和黏性应力差产生的加速度，其中：

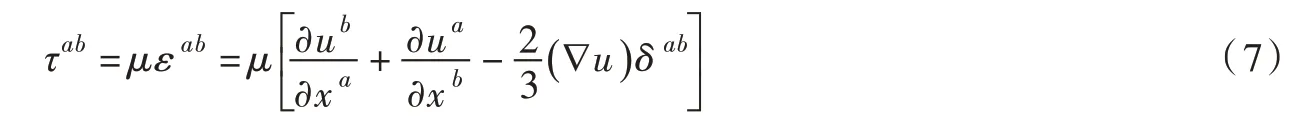
式中：上标a 和b 表示坐标方向；p 为压强；δ为狄拉克函数；τ为黏性剪应力；μ为黏性系数；ε为剪应变率。

综上，SPH 离散化形式可写为［6］：

3.3 溶质扩散方程在孔隙尺度下，流体质点间的溶质交换仅表现为分子扩散，采用经典的Fick 扩散方程描述，其控制方程为［1］：

式中De为分子扩散系数。

将弥散系数考虑为常数，参考热传导方程［16-17］的离散形式，离散化式（10），得到在粒子点xi处的溶质迁移二维近似表达式：

3.4 人工压缩性对于不可压缩流体，采用实际的状态方程会导致计算时间步长过小，因此理论上不可压的流体在数值计算时一般考虑为微可压缩流体。这里所采用的人工压缩性状态方程为［8］：

式中：c 为人工速度，一般取最大流速的10 倍。

为保证粒子位置的相对齐整，采用Monaghan［18］推导的“XSPH”方法平均化粒子的相对速度：

式中γ 为常数，常取0.3。XSPH 方法可有效保持粒子的运动速度与相邻粒子的平均速度相近，从而避免相近粒子的相互穿透。

3.5 固液边界处理SPH 计算中，常用的边界处理方法有：边界力法、镜像粒子法、耦合边界法等。为处理多动介质中复杂的固液边界，本文采用的边界力模型为描述粒子间相互作用的Lennard-Jones 力模型［2，5］：

式中：r0为截止距离，流体质点只有运动到这一距离以内，才会受到边界力的作用；n1、n2为常数，通常取12 和4；F 为经验参数，根据具体问题确定，一般取为与速度最大值的平方相等的量级［2］。

3.6 时间步为保证数值计算的稳定性，时间步长需满足CFL 条件（Courant-Friedrichs-Levy condition）。对SPH 的水动力模型，需满足下列规则［8，10］：

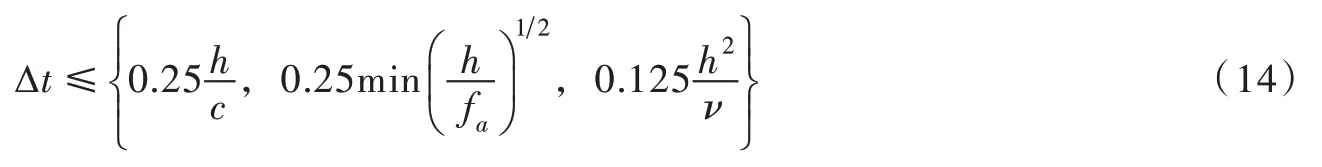
式中：h 为光滑长度；c 为人工速度；fa为粒子加速度，ν=μ/ρ为运动黏度。

而对于扩散问题，时间步长则需满足［16-17］：

式中：β为计算参数，相关研究表明当β＜0.15 时计算是稳定的，一般可取β=0.1。计算中，密度、速度和位置时间积分采用具有二阶精度的跳蛙法推进［10］，浓度的时间积分则采用Euler 公式［17］。

4 仿真实验方法

首先介绍无量纲数Peclet，Peclet 数表示对流与扩散的相对比例［19］，常用P 或Pe 表示：

其中：u 为渗流速度，m/s；R 为特征长度，m；De为分子扩散系数，m2/s。Pe 数增大，输运中分子扩散输运比例下降，对流输运增大。当Pe 小于1 时，分子扩散占优；而当Pe 超过100 时，可基本忽略分子扩散的影响［20］。

4.1 模型处理对计算模型做如下规定：（1）流场内饱和；（2）多孔介质骨架不可压缩且不发生移动；（3）假定流体在多孔介质中流速稳定，不考虑重力对流动的直接影响。

为使边界条件实现速度控制和溶质浓度控制，将进入流场前后（图2中L1 至L2，L3 至L4）范围内视为边界区域（边界区域尺寸的选取需保证流场内流体粒子的影响域完整），进入该区域内的流体粒子在水平方向的速度值设定为注入速度、浓度值设定为注入浓度，其他性质与正常流体粒子相同。为实现下游流出粒子的重复利用和溶液的持续注入，设计了粒子传输模块：统计越过L3 界面的粒子个数记为Nout，以及粒子携带的溶质浓度Cout，并将流出L4 界面的粒子初始化后迁移至注入端，以此实现模拟流体持续流动。流场的上下界面均为周期边界［9］，越过下边界的粒子会进入上边界，即可视作流场沿周期边界的正交方向重复延伸。

图2 二维多孔介质流场的边界处理示例

定义孔隙水体积数pv（Pore water volume），它是无量纲时间变量，反映流出水体积与总孔隙水体积的比值［21］，在宏观尺度下，pv与时间t 有以下关系：

式中：u 为注入速度，m/s；A 为横截面积，m；Vp为孔隙体积。在多孔介质中，Vp=φV，φ为孔隙率，V 为总体积，m3；而在规则流场中有，pv=ut/L，L 为流距，m。

在这里，pv即为流出介质区域的粒子总数Nout与流场内总流体粒子数Ntotal的比值：

4.2 计算过程首先需将计算域离散为粒子点，并赋初值，包括坐标、质量、密度、光滑长度等基本参数，以及设定粒子类别（如图2中的流场内流体粒子、两侧边界区域内流体粒子以及固相粒子）。在每一时间步中，先采用N-S 方程的SPH 离散形式（式（5）、式（8）、式（11）、式（12））计算得到所有粒子的速度、加速度、坐标、密度、压力等，对进入固相粒子影响域范围内的流体粒子还需计算罚力（式（13）），再由溶质扩散方程（式（10）），计算得到粒子点的浓度值。最后根据粒子的坐标，判定是否进入两侧的边界区域内，更新粒子类别；若粒子位置超出最右侧边界（L4），则将其参数初始化（密度、压强恢复初始值）后迁移到左侧注入端（L1）。对于两侧边界区域内的粒子，需规定水平速度等于注入速度，左侧注入区（图2中L1 至L2）内粒子浓度等于注入浓度，再进入下一时间步。时间步的推进方式如3.6 节所述。

4.3 解析解检验若将图2中的流场区域全部填充为流体粒子，则该算例可简化为一维定解问题。基于平均流速的一维多孔介质对流-弥散方程为［1，21］：

式中：D 是水动力弥散系数，m2/s； u 为平均流速，m/s。其中D=De+Dm，De和Dm分别为分子扩散系数和机械弥散系数。一般认为［21］，Dm=αuλ，α为机械弥散度，m，简称弥散度，参数λ一般取1［22］。

假定多孔介质初始浓度为0，注入浓度为C0的溶液，边界条件为：C（0，t）=C0，C（∞，t）=0，则该一维注入问题的解析解为：

表1 计算参数

式中：erfc 函数为互补误差函数，在Matlab、Excel 等计算软件中均有内置函数可直接调用。

5 高Peclet 数流场模拟

5.1 多孔介质孔隙流的模拟计算中采用的多孔介质为堆积圆形砂砾土，假定为理想的交错堆积方式。选取某一理想正方形截面作为研究对象，将其置入单向注入的流场中。

模型处理方法如4.1 节所述，左右两侧为速度控制的边界区域，上下均为周期边界条件（如图2），流出右侧界面的粒子将被初始化后迁移至注入端，该算例可视为恒定流速黏性流体穿透二维多孔介质薄层的仿真实验。

图2中选用的填充颗粒直径在1.0～2.5 mm 之间，介质域为0.012 m×0.012 m 的方形区域，注入流速恒定u0=0.04 m/s，孔隙率φ=0.58，粒子初始间距为0.0002 m，时间步间隔Δt=0.00002 s。计算中固相粒子密度按2 g/cm3计算，位置固定，其加速度、速度以及压强值始终为0，计算结果见图4至图7。由图4可知，在x 方向上，流速大的区域集中在基质颗粒之间的孔道内，孔道内流速分布具有抛物线形泊肃叶流特征，不同粗细的孔隙通道内质点流速有明显差异。

图5分别为注入0.02s、0.05s、0.1s 以及0.2s 后携带溶质的流体质点在多孔介质中的弥散现象。若追踪注入界面上分布的若干颗粒子的运动轨迹，可得到图6所示的流体粒子迹线图（图中将越过周期边界的粒子画在了边界外侧）。根据该迹线图，可计算得到该多孔介质的迂曲度［9］：

图4 速度矢量与等值点图

图6 流体粒子迹线图

若溶质分子扩散系数De= 1.35×10-9m2/s（取为NaCl 在20 ℃水中的扩散系数），在多孔介质中计算Pe 数的特征长度一般取为颗粒粒径［9］，可得Pe 数3×104～7.4×104≫100，故忽略分子扩散的影响。则水动力弥散系数D=Dm=αu，弥散度α的大小可采用式（20）对穿透曲线进行曲线拟合得到（如图7）。弥散度与迂曲度、孔隙率的关系将在5.3 节统一讨论。

图7 介质末端的穿透曲线及弥散度的拟合曲线（R2=0.98）

5.2 速度差对弥散度的影响为进一步研究溶质渗透迁移过程中速度差对机械弥散效应的影响，建立了三段理想化的孔隙通道模型，如图8所示。三段曲折管的管径、容积相同，以保证三种曲折方式中流体质点的迂曲路径基本一致。仿真实验中，从左侧注入含某溶质的等浓度溶液，边界区域粒子速度按泊肃叶流速方程设定［8］：

本算例中，注入和流出端管径l=1 mm，动力粘度ν=10-6m2/s，单位质量的传动力F=0.8 m/s2，由式（22）可求得相应的中心水平流速u0=0.1 m/s，雷诺数Re=100，若分子扩散De= 1.35×10-9m2/s，得Pe =7.4×105≫100，故只考虑机械弥散。以上三种曲折管在注入恒定流速的黏性流体时，产生了明显速度分布差异，其穿透曲线如图9所示。

图8 溶液注入的机械弥散过程

图9 三种曲折管流场的穿透曲线图

由图9中溶质的穿透曲线，可拟合得到表2中弥散度α。根据表2中弥散度与粒子流速变异系数的变化趋势，可知在迂曲路径相同的情况下，流体质点的速度差越大，机械弥散效应越显著，表现出更大的弥散度。

5.3 弥散度与多孔介质结构参数的关系弥散度被认为是反映多孔介质骨架结构特征的物理量，孔隙的疏密程度以及颗粒的排布方式等均可影响多孔介质的弥散效果。常用于描述多孔介质的结构参数包括孔隙率、颗粒不均匀系数、迂曲度等，但这些参数与弥散度的联系未见有具体的研究。因此，本节将讨论多孔介质的孔隙率φ，颗粒不均匀系数Cu和迂曲度τ与弥散度α的相关性。这里颗粒的不均匀系数Cu=d60/d10，反映了大小不同粒组的分布情况，d60和d10通过对颗粒粒径的插值近似取值。

类似图2生成一系列具有随机粒径分布和不同孔隙率的二维多孔介质计算单元，进行了多组多孔介质溶质穿透仿真实验，得到的多孔介质结构参数与弥散度的关系如图10所示。

速度差的存在，使得携带溶质的流体质点在单位时间内的迁移距离存在差异，由此导致了溶质弥散现象的产生。随着孔隙水流速分布的离散性越大，这种弥散作用更加强烈，因而弥散度与速度的变异系数大致成正相关（图10（a））。

表2 三种曲折管弥散度比较

图10 多孔介质结构参数与弥散度的关系

在孔隙率、弥散度和迂曲度的关系中，目前，已有大量的实验结果和理论依据来证明迂曲度随孔隙率的增大而减小［23-24］（图10（b））。由图10（c）（d），随着孔隙率的增大，弥散度有减小的趋势；此外随迂曲度增大，弥散度大致线性增加。这是由于孔隙率降低，将使得基质颗粒间的孔隙通道减小，导致流体质点的渗透迁移面临更多阻碍，从而迂曲度增大。而迂曲度越大，孔隙流体迂回曲折的路径越复杂，弥散效果则越显著，弥散度越大，因而弥散度的变化趋势与孔隙率呈负相关；图10（e）中，随着迂曲度的标准差增大，流体质点穿透单位长度的多孔介质时，所走过的迂曲路径差异越大，因而弥散度越大。图10（f）中，随颗粒不均匀系数增大，弥散度有增大趋势。

综上，根据多组随机粒径的二维多孔介质溶质穿透仿真实验结果，迂曲度、孔隙率、迂曲度标准差以及颗粒不均匀系数与弥散度均存在明显关联。迂曲度作为反映多孔介质内部孔隙通道复杂程度的重要参数，可通过实验手段测量［23］；且迂曲度与多孔介质弥散度相关性较好，今后可进一步研究采用迂曲度定量估算弥散度的可能性。

6 结论

本文基于SPH 方法，从溶质迁移扩散的物理本质出发，实现了孔隙尺度下多孔介质溶质弥散的仿真实验。仿真实验设计中，充分利用了SPH 方法的拉格朗日粒子特性，可便捷得到仿真实验中的质点速度分布、迂曲路径以及溶质穿透曲线。此外，采用周期边界和上下游粒子传输模块可实现介质域的重复拓展和溶液的持续注入功能。研究中，通过建立三段迂曲路径一致的孔隙通道模型分析速度差对机械弥散效应的影响。然后在多组溶质穿透多孔介质的仿真实验基础上，讨论多孔介质结构参数对弥散度的影响。结果表明：（1）在控制流体质点迂曲路径相同的情况下，流动速度差对溶质机械弥散效应仍有显著影响，流速的变异系数越大，则介质的弥散度越大；（2）弥散度与迂曲度、迂曲路径差以及不均匀系数大致呈正相关，与孔隙率呈负相关；（3）鉴于迂曲度与多孔介质弥散度相关性较好，且迂曲度作为反映多孔介质内部孔隙通道复杂程度的重要参数可通过实验手段测量，在今后的研究中可考虑采用迂曲度定量计算弥散度。

由于多孔介质本身的复杂性，介质弥散度与结构特征参数的关系仍需大量研究支持，而在实验中涵盖各特征参数往往十分困难，本文仅提供了一种采用SPH 进行孔隙尺度数值实验的思路。此外，目前对弥散度影响因素的认识较不明确，本文研究结论也可为理论模型的参数选择提供参考。