Surface plasmon polaritons generated magneto-optical Kerr reversal in nanograting∗

Le-Yi Chen(陈乐易), Zhen-Xing Zong(宗振兴), Jin-Long Gao(高锦龙),Shao-Long Tang(唐少龙),†, and You-Wei Du(都有为)

1Collaborative Innovation Center of Advanced Microstructures,Nanjing National Laboratory of Microstructures,Jiangsu Key Laboratory for Nanotechnology and Department of Physics,Nanjing University,Nanjing 210093,China

2Department of Physics,School of Biomedical Engineering and Informatics,Nanjing Medical University,Nanjing 211166,China

Keywords: magneto-optics,surface plasmons,magnetoplasmonics,magneto-optical devices

1. Introduction

With the rise of metamaterials,magnetoplasmonics have experienced considerable development, and shows great potential applications in various fields such as all-optical magnetic data storage,[1,2]optical isolators and modulators,[3,4]and ultraprecise distance probe.[5]Gradually, one is not satisfied with limiting their visions on concentrating the electromagnetic energy of light at the interfaces to enhance magnetooptical (MO) effect.[6-11]More research has began to turn to the investigation of the sign of MO signal and the change of sign.[12-14]Especially, after Maccaferri et al. reported their magnetoplasmonic biochemical sensor showing a raw surface sensitivity of two orders of magnitude higher than that of the traditional nanoplasmonic sensor,[15]The MO Kerr rotation reversal has become a new focus thanks to its potential application in ultra-high precision environmental detection.[16,17]MO Kerr rotation reversal was found successively in isolated magnetic nanodisks,[15,18,19]and in two-dimensional magnetic metal lattice.[20]It has been known that magneto-optical Kerr rotation is due to the transverse magnetic(TM)and transverse electric(TE)mode conversion in the material,caused by spinorbit(SO)coupling. The mode conversion between the amplitude and phase lag determines the magnitude and sign of Kerr rotation. The Kerr rotation reversal can be achieved when the phase lag between TE and TM components of the reflected light is an odd integer multiple of π /2.[19]Previous studies usually used the additional phase of the excitation of the localized plasmons to meet the above phase condition in randomly distributed nanodisks.[19]Further,the phase of localized plasmons can be modified by surface plasmon polariton(SPP)via forming Fano resonance in ordered nanostructures to achieve the adjustable Kerr rotation reversal.[20,21]

In this paper, we show that MO Kerr rotation reversal can also be observed in the wavelength positon with only SPP mode existing.We confirm the experimental results in Co gratings and three-layer metal grating Ag/Co/Ag nanogratings and demonstrate that it is the SPP mode existing independently,providing the necessary phase condition for MO Kerr rotation reversal.

2. Sample fabrication

The nanograting samples were fabricated as follows.First, a 100-nm-thick photoresist (Allresist, AR P-3170) was spin-coated on a silicon substrate and followed by a pre-bake at 95°C for 1 min. Then the photoresist film was patterned by a home-made Lloyd’s-Mirror interference lithography system. Afterwards, the exposed photoresist film was immersed in a developing solution (Allresist, AR 300-26 diluted 1:5 with deionized water)for 45 s. A grating pattern with an appropriate slit width can be produced by properly adjusting the exposure dose. We can achieve the grating patterns with different periods via changing the incident angle of the laser on the photoresist film during the exposure stage. The period of the fringe pattern can be given by λ/(2sinθ),where λ is the laser wavelength and θ is the half angle of intersection of the laser beams. In the next step, a 50-nm-thick cobalt film was deposited on the photoresist grating in turn by DC magnetron sputtering with an Ar pressure of 0.5 Pa.By changing the incident angle,we obtained two Co nanograting samples with different periods,named Co385(with the period L=385 nm,the width of the strip d=210 nm)and Co325(with L=385 nm,d =180 nm). We then replaced the cobalt film with a threelayer composite film of Ag/Co/Ag in the DC magnetron sputtering stage, and obtained another two grating samples, referred to as ACA385 (with L = 385 nm, d = 210 nm) and ACA325(with L=325 nm,d=180 nm),respectively.All the geometric parameters of the Ag/Co/Ag nanograting samples are described in Fig.1(a). The top view of all four nanograting samples are shown in Figs.1(b)-1(e).It is clearly seen that the nanogratings without obvious defects show good periodicity. The cross-sectional profile of each sample gives the height of the gratings h=100 nm.

Fig.1.Topography of the Co grating and Ag/Co/Ag three-layer metal nanograting samples.(a)Schematic illustration of Ag/Co/Ag nanograting samples. Upper Ag layer of each sample is 5-nm thick,mid Co layer is 10-nm thick,and lower Ag layer is 35-nm thick. The total thickness of three layers of metal is fixed at 50 nm, which is the same as those of Co grating sample. (b)-(e) Atomic force microscopy image of the nanograting samples ((b) sample Co385, (c) sample ACA385, (d) sample Co325, and (e) sample ACA325, fabricated by interference lithography and DC magnetron sputtering. Cross-sectional profile of each sample is drawn along white reference line.

3. Experimental results and discussion

The optical reflectivity of the three-layer nanograting sample is given priority because it is closely related to the surface plasmon (SP) mode on the grating surface. The reflectivity was measured by spectroscopic ellipsometer (J. A.Woollam M-2000) with a white light source focused into a spot with a diameter of approximately 0.5 mm. The reflectivity spectra were obtained by the ratio of the zero-order reflective signal of the samples to a base line of the light source. For one-dimensional gratings, there is no spatial confinement in the direction perpendicular to the lattice vector of the grating.So when grating samples are impinged by the incident light in the configuration shown in Fig.2(b),the SPP mode cannot be excited because of the momentum mismatch.[1]However,if the incident light is s-polarized (the electric vector is perpendicular to the incident plane; i.e., along the lattice vector of the grating),the free electrons at the interface can be driven by the electric field of the light, and thus exciting the localized surface plasmon (LSP) mode. Figures 2(a)-2(d) show the results of the four grating samples. In Figs.2(c)and 2(d),there is only one set of dips in each figure. Both of the sets of dips have weak dependence on the incident angle,which is considered as a feature of the LSP excitation.[20]They show an accurate relation corresponding to the simulation results of extinction cross section of the single nanostrip with the same width as the grating. The simulation was carried out by the discrete dipole approximation(DDA)method combined with Mie theory.[22]These provide sufficient evidence for the LSP mode excitation, and the positions are located at 371 nm for ACA385 and 355 nm for ACA325,respectively. For Co grating samples, the simulated extinction cross section peaks are almost invisible due to the great Ohmic loss in ferromagnetic metal, as shown in Figs. 2(a) and 2(b). The dips with obvious LSP characteristics cannot be observed either. Thus, the LSP modes in Co grating samples are considered negligible.When the p-polarized light with the magnetic vector perpendicular to the incident plane is chosen as the laser source, it is well known that SPP modes can be excited via grating coupling in the configuration with the incident plane along the grating lattice vector,which is shown in Fig.2(e). Both of the sets of grating samples exhibit the behavior of SPP mode in the reflectance spectrum. It can be seen from Figs. 2(e)-2(h)that the dips each have significant red shift as the incident angle increases in their respective wavelength range,from about 600 nm to 700 nm for Co385 and ACA385 samples,and from about 500 nm to 600 nm for Co325 and ACA325 samples,which accord well with the calculated SPP excitation positions by using the momentum match condition in Fig.2(i). It is worth mentioning that the SPP excitation position seems to have more to do with the period of the grating than the dielectric tensor difference between silver and cobalt in the visible region. In conclusion, we can believe that the dips in the reflectance spectra in Figs.2(e)-2(h)are derived from the excitation of SPP mode.

Fig.2. Reflectance spectra of Co and Ag/Co/Ag nanograting samples. Measured reflectivity with s-polarized light in the light path configuration shown in inset in panel(b)at different incident angles(right axis)and calculated extinction cross section of a single strip(left axis)for(a)sample Co385,(b)sample Co325, (c) sample ACA385, and (d) sample ACA325. Measured reflectivity with the p-polarized light in the light path configuration shown in inset in panel(e)for(e)sample Co385,(f)sample Co325,(g)sample ACA385,(h)sample ACA325. (i)Calculated incident angle dependence of spectral position to excite SPPs at the air-metal(Ag,Co)interface.

In the MO measurement, an external magnetic field up to 1.6 kOe (1 Oe=79.575 A·m-1) was applied to a longitudinal Kerr configuration. The p-polarized light with a fixed incident angle at 45°struck the surface of the grating sample with the incident plane along the grating lattice vector,which is sketched in the inset of Fig.2(e). The results of all the four grating samples are shown in Fig. 3(a), and the MO Kerr rotation reversals are obvious. More evidences for Kerr reversal are provided by the Kerr rotation loop at specified wavelengths of each sample in Fig. 3(b). Intuitively, the Kerr reversals can be divided into two groups: around 525 nm for Co325 and ACA325 and around 680 nm for Co385 and ACA385. It seems to have more to do with the period of the grating than the material and to be consistent with the excitation region of their respective SPP modes. However, we still have to consider the influence of the possible LSP mode, because the ppolarized light with an oblique incidence has an electric component along the grating lattice vector,which probably can excite the LSP mode,which is similar to the s-polarized situation in Figs. 3(a)-3(d).[20]For the Co grating samples Co385 and Co325, the LSP modes are almost invisible due to the great Ohmic losses as mentioned above. For the Ag/Co/Ag grating samples ACA385 and ACA325, the LSP modes are located around 350 nm,and the noble metal silver exhibits the excellent properties of LSP,embodied as the sharp peak in the dispersion curve of the extinction cross section in Figs.2(c)and 2(d). It also means that the LSP modes in Ag/Co/Ag grating samples are concentrated in a very narrow UV range,and dif-ficult to influence the Kerr reversal at 685 nm for ACA385 and 534 nm for ACA325. Therefore,it can be determined that the Kerr reversal is caused by SPP mode independently in both Co grating sample and Ag/Co/Ag grating sample.

Fig. 3. (a) Longitudinal Kerr rotation of Co and Ag/Co/Ag nanograting sample with p-polarized light incidental 45°. Longitudinal Kerr rotation of flat Co film is plotted as a contrast. (b)Longitudinal Kerr rotation loops of nanograting samples at specified wavelengths with p-polarized light incident at 45°.

In a previous study, Maccaferri et al. proposed a model of two orthogonal damped harmonic oscillators to explain the polar Kerr rotation reversal in a nanosized Ni disk.[19]The displacement of the conduction electrons on the nanodisk leads to an electromagnetic restoring force,which gives rise to an LSP mode and additional phase lag of π/2 between TE and TM components of the reflected light at the LSP excitation position. This can be extended to the qualitative explanation of why the SPP mode can give rise to the Kerr reversal. The ppolarized light with an oblique incidence has an additional zaxis electric component perpendicular to the grating/air interface besides the in-plane component along x direction,which is shown in Fig.4. The z-axis component can lead to a charge accumulation at the metal/air interface. This is essential for the emergence of SPPs. When the momentum match condition is satisfied, the electromagnetic field energy of the incident light can be coupled to the electron motion,leading to the collective oscillation of the free electrons and forming the surface TM wave propagating along the interface;i.e.,SPP mode.

In this physical process,the charge accumulation at the interface gives rise to the source of electromagnetic restoring force.Then,the motion of the electron along the z direction is given as follows:

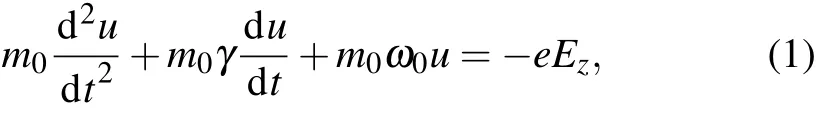
where γ is the frictional force modelled damping rate, Ezis the z-axis electric component of the incident light,and e is the electric charge quantity of electron. When the SPP mode is excited(ω =ω0),the velocity resonance of the free electrons creates an energy absorption peak in the spectrum and a phase lag of the oscillation relative to the driving force as given below.

It means that there is an additional phase difference of π/2 between the polarization and the incident light along the z direction when the SPP mode is excited.

Fig.4. Process of incident p-polarized light being reflected on nanograting surface and the damped harmonic oscillator model in z direction.

In the case of longitudinal Kerr configuration,the permittivity tensor of an MO active material can be described as an antisymmetric matrix with εxx≈ εyy≈ εzzand εyz=-εzy=ig.The remaining elements are zero. Thus,the electron momentum along the z direction can be transferred to the y-axis via SO coupling with an intrinsic phase determined by the intrinsic property of the material.So,the additional phase difference of π/2 is further transferred in the y direction and finally in the TE component of the reflected light.Then we consider the TM component of the reflected light. When the light impinging on the grating surface at the incident angle of α along the direction sketched in Fig.4,the grating diffraction equation can be expressed as

Note that for our subwavelength grating samples with L ＜ λ,the phase difference can never reach 2π. Equation(3)can be satisfied only when α =βm=0, i.e., in the case of specular reflection. Thus, the TM component of the reflected light is determined by Fresnel formula and has nothing to do with the electron motion along the z direction in the metal layer of the grating. The exact phase lag between the TE and TM component is complicated, but can be experimentally reflected in the MO Kerr rotation. From what we have described in this paper,it can be concluded that an additional phase difference of π/2 exists between the TE and TM component when the SPP mode is excited, compared with other usual wavelength region,thereby leading to the Kerr reversal.

4. Conclusions

In this work, using interference lithography and DC magnetron sputtering, we have fabricated Co and Ag/Co/Ag nanogratings of different periods. We use different means to exclude the possible influence of LSP mode in the gratings of the two materials,and experimentally confirm that the SPP mode in our grating samples can gives rise to the reversal of MO Kerr rotation. We also give it a qualitative explanation that it is the charge accumulation at the interface between the grating surface and air that acts as the electromagnetic restoring force to contribute additional phase when the SPP mode is excited. Producing Kerr reversal via the excitation of SPP mode gives us a new approach to designing and fabricating the MO-based biochemical sensors, which have shown ultrahigh sensitivity to the surrounding refractive index and unlimited value of figure-of-merit. Furthermore,it can be predicted that when compared with the LSP mode caused Kerr reversal,the SPP mode-induced Kerr reversal should have good tunability due to the more flexible excitation wavelength and better compatibility with waveguide mode.[23]We hope that our work will conduce to the development of the highly sensitive MO-based bio/chemosensing sensors.