多步法阿当姆斯方法的稳定性分析

李凯

(中国传媒大学信息科学与技术学部，北京 100024)

1 引言

在以往对微分方程初值问题的研究中，我们对一个数值方法进行理论分析优劣时，常常对相容性、收敛性等有关方面进行分析，考查一个方法对舍入偏差的敏感性，这便是数值稳定性问题，这不单与计算公式有关，并且与微分方程性质有关。

2 线性多步法的构造——数值积分法

讨论常微分方程初值问题

(1)

的数值求解，其中f为t和u的已知函数，u0为给定的初值。易知

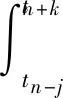
(2)

我们用被积函数f(t，u(t))的q次Lagrange插值多项式

用来近似代替式(2)中的被积函数，这里{ti}为等距的插值点列，h=ti+1-ti，而

于是得到近似公式

(3)

其中

(4)

在式(3)中，用un代替u(tn)，仍用fn表示f(tn，un)，用等号代替≈，则得到线性多步方法公式

(5)

3 阿当姆斯显式方法

对k，j和q的差别选择，得到不同类型的公式。对k=1，j=0和q=0，1，2，…，可以得到阿当姆斯显式方法：

un+1=un+h(βq0fn+βq1fn-1+…+βqqfn-q)，

(6)

其中，公式系数如表1，最常用的是q=3的情形。

表1 阿当姆斯显式方法系数表

4 阿当姆斯隐式方法

对k=0，j=1和q=0，1，2，…，可以得到阿当姆斯隐式方法(用n+1代替n)

un+1=un+h(βq0fn+1+βq1fn+…+βqqfn-q+1)

(7)

其中，公式系数如表2，最常用的是q=3的情形。

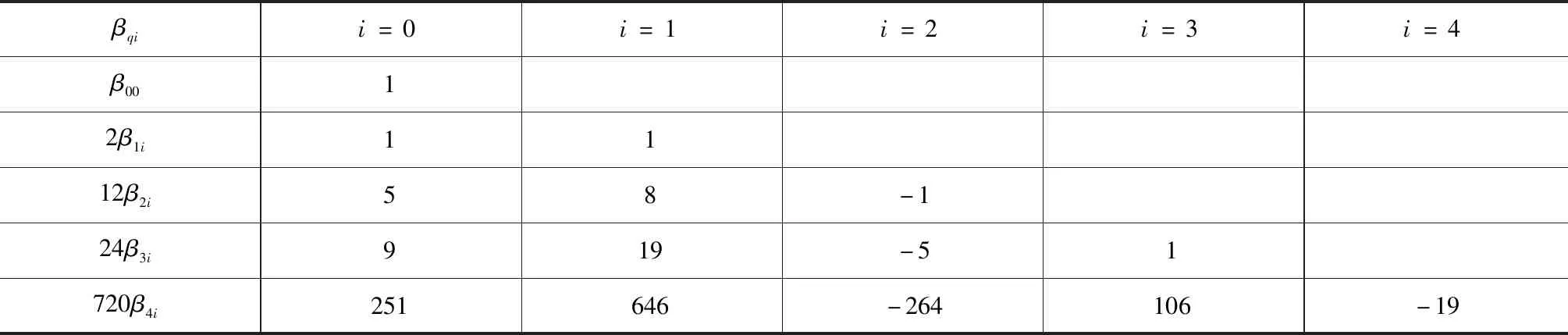
表2 阿当姆斯隐式方法系数表

显然，公式(7)不是n+1的一个明显表达式，而是以n+1为未知量的非线性方程。

5 两种多步法的稳定性以及稳定区间

易得知两种公式不同步数不同阶数情况下的误差常数如表3、表4，其中q为阶数，cq+1为误差常数。

表3 阿当姆斯显式方法不同阶下的误差常数

表4 阿当姆斯隐式方法不同阶下的误差常数

对于k步阿当姆斯显式及隐式方法的绝对稳定域较为复杂，通常采用根轨迹法，暂且不作讨论，把它们的绝对稳定区间分别记为(θA，0)及(θB，0)，则其中θA及θB之值可列表如下。

k1234θA-2-1-116-310θB-∞-6-3-9049

6 总结

通过利用Matlab编程计算分析及以上表格得出：同阶的隐式方法与显示方法相比，步数少1，误差常数的绝对值小5-13倍，绝对稳定区间又大过10倍以上；总的来讲，阿当姆斯隐式方法优于显式方法。