一阶常微分方程初值问题的数值解法
2019-08-16支越
支越
(中国传媒大学信息科学与技术学部,北京 100024)
1 引言
基于上述假设,根据常微分方程的理论,可知初值问题在区间[t0,T]上有唯一的连续可微的解u(t)。
2 数值方法求解实例
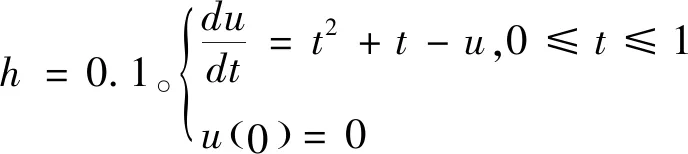
2.1 解析解
解析解(准确解):u=-e-t+t2-t+1。
2.2 欧拉法
欧拉法公式:un+1=un+hf(tn,un)。
2.3 梯形法
2.4 改进欧拉法
2.5 RK法
其中Wi,αi,βij均为待定系数,实际计算时,用un代替u(tn),上述公式称为s级RK方法。
2.6 Adams法
Adams方法是一种线性多步法。
Adams四阶预测—校正格式(PECE),这是一个四步方法,计算un+4时要用到un+3,un+2,un+1,un,因此它不是自开始的,一般需要四阶RK法为其提供出发值:u1,u2,u3。(p为阶数,p=4)
Efn+4=f(tn+4,un+4)
3 实例的各类数值解法比较
利用VC++6.0,运行各类数值解的C语言程序,求解本文中的实例,求解区间[0,1],步长h=0.1,结果如表1所示。
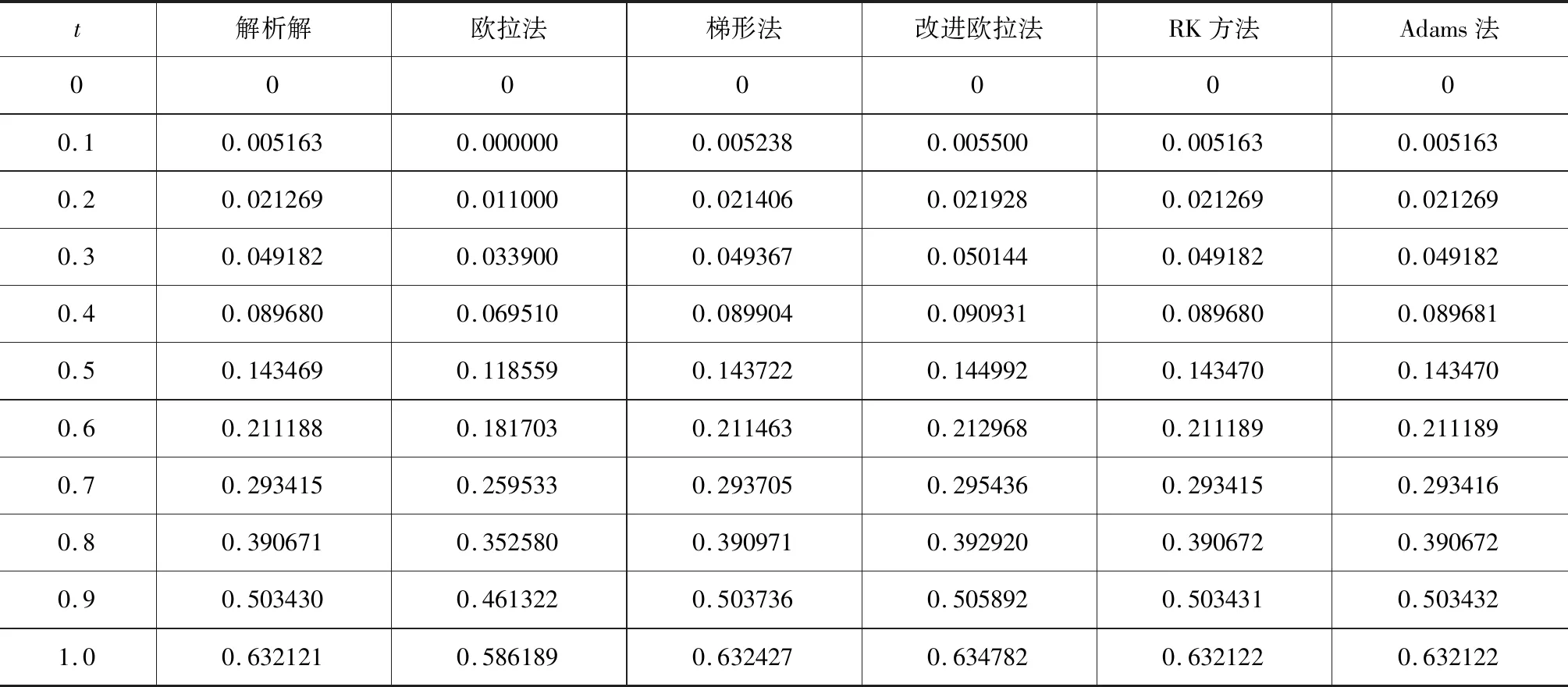
表1 数值解法
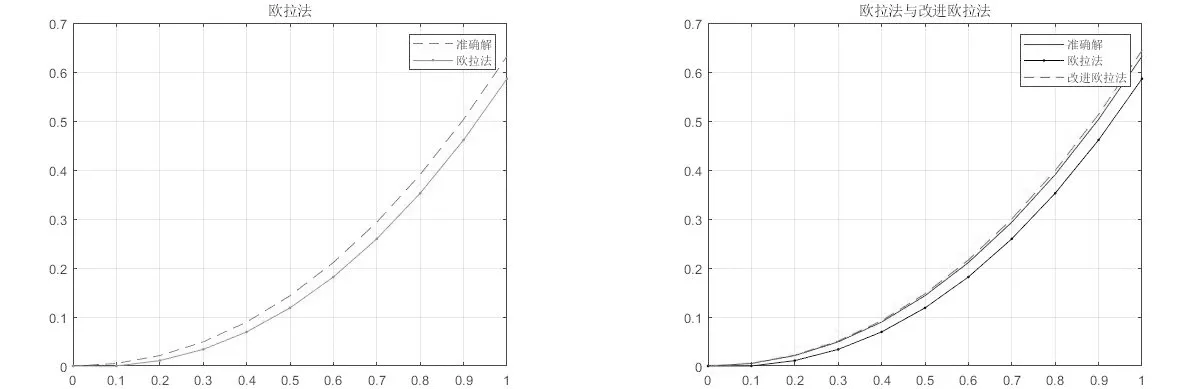
图1 欧拉法 图2 欧拉法与改进欧拉法

图3 四阶经典RK法 图4 Adams四阶预测-校正格式
从以上图1-4可以观察出,欧拉法的数值解与解析解相差较大,用梯形法和改进欧拉法求得的数值解优于欧拉法,但弱于四阶经典RK法和Adams四阶预测—校正法,RK法和Adams法的数值解非常接近解析解。
4 结论
欧拉法用均差代替导数进行计算,微分方程的解u=u(t)称作它的积分曲线。从几何上来解释欧拉法,欧拉法做出的折线PnPn+1是落在积分曲线u=u(t)上的顶点Pn的切线,顶点Pn+1明显的偏离了积分曲线u=u(t),可见欧拉法是粗糙的,用欧拉法求出的数值解与解析解相比较,误差较大。
梯形法用迭代法求解,欧拉法为其提供迭代初值,但是迭代反复,计算量大。改进欧拉法简化了算法,明显改善了精度。
四阶经典RK法是RK法中常用的数值解法。关于Adams四阶预测—校正格式,一般需要四阶经典RK法为其提供初值,编程代码相较于前面的方法,计算量明显增多,但精度更高,数值解很接近解析解。
