正则迹范数在人脸识别中的应用

林智鹏 简彩仁 周书伟

摘 要：人脸识别技术得到了广泛研究与开发应用，人脸识别问题已成为模式识别和图像处理中最热门的研究主题之一。文中提出正则迹范数人脸识别法：利用正则迹范数改进基于表示理论的分类法。该方法通过正则迹范数平衡L1范数的稀疏性质和L2范数的聚集性。在4个公开人脸识别数据集上的实验表明，该方法可以较好地提高人脸识别准确率。

关键词：人脸识别;迹范数;分类;稀疏;聚集;图像处理

中图分类号：TP311;TP371文献标识码：A文章编号：2095-1302（2019）07-00-03

0 引 言

由于人脸的自然特性，人脸识别（Face Recognition）已经成为身份认证的重要生物特征技术，在军事、国防、公安和日常生活等领域得到了广泛应用。随着大数据及计算机技术的迅速发展，人脸自动识别技术得到了广泛研究与开发，人脸识别成为近30年模式识别和图像处理中最热门的研究主题之一。人脸识别的目的是从人脸图像中抽取人的个性化特征，并以此来识别人的身份，在20世纪90年代初，人脸识别的研究随着特征脸方法的引入而流行起来[1]，人脸识别研究已经引起了科研人员的浓厚兴趣，提出了诸多识别方法，并取得了较大成功[2-4]，但由于人脸采样环境的复杂性，如图像质量不清晰、人脸表情、面部遮挡等，使得研究具有鲁棒性能的人脸识别方法仍然具有重要的意义。

许多基于经典的分类方法在研究人脸识别问题上存在局限性，比如k最近邻分类法基于欧式距离的大小分类难以克服人脸图像数据集高维数和非线性等困难;支持向量机是一种经典的分类方法，但由于需要训练分类器，容易造成过拟合问题。伴随着模式识别技术的不断发展，许多基于流形学习和稀疏表示的分类方法被提出，并且被广泛应用于人脸识别研究中。以稀疏表示分类法为代表的基于表示理论的分类方法[5-7]，利用训练样本表示测试样本，充分考虑了所有样本对分类的影响，可以在一定程度上克服人脸图像数据的高维数和非线性等困难，不仅如此，基于表示理论的分类方法无需训练分类器，可以避免传统分类方法的过拟合问题，因此基于表示理论的分类方法在人脸识别、肿瘤识别等方面的研究中得到了广泛应用。稀疏表示分类法（SRC）[5]、最小二乘回归分类法（LSRC）[6]以及非负最小二乘回归分类法（NNLS）[7]等都是基于表示理论的分类法，它们的区别在于正则惩罚项或约束条件的不同：稀疏表示分类法（SRC）利用L1范数的稀疏性质构建分类器，最小二乘回归分类法（LSRC）利用L2范数的聚集性构建分类器，非负最小二乘回归分类法（NNLS）利用表示系数的非负限制构建分类器。

本文研究了基于表示理论的人脸识别方法，借鉴文献[8-9]，迹范数可以同时保持L1范数的稀疏性质和L2范数的聚集性优点。基于迹范数的人脸识别方法通过正则迹范数保持表示系数的稀疏性和聚集性。

1 相关研究

基于稀疏表示、最小二乘回归和最近邻子空间准则提出了基于正则迹范数的分类法。

1.1 最小二乘回归

假设y是未知类别标签的人脸图像样本，X是已知类别标签的人脸图像样本训练集，有n个训练样本，m个图像属性，其中mn，用已知类别标签的训练集表示未知类别标签的样本。

式中xi为第i个训练样本，由于mn，是一个超定方程，因此求解该公式的精确解无意义，考虑如下最小二乘回归

模型：

得到该模型的解析解：

1.2 稀疏表示

稀疏表示通常表示为如下求解稀疏系数w的问题：

式中||w||0是向量w的L0范数，表示向量w非零元素的数量。求解该问题较难，因此可将问题转化为求解L1的问题：

式中||w||1是向量w的L1范数，即向量w非零元素绝对值的和，可以扩展为允许有噪声的模型：

式中λ>0，是正则参数，Kim等人给出了一种快速计算稀疏表示模型的方法[10]。

1.3 最近邻子空间准则

最近邻子空间准则[1]通过分类重构测试样本的方法对测试样本进行分类。假设人脸图像数据集有K个类别{l1，l2，…，lK}，对一个人脸图像数据样本y求解系数向量w，对每一个类计算如下的度量余量：

式中δk（w）：Rn→Rn，计算得到类lk的系数，其第j个元素定义为：

样本y所属的类：

2 基于正则迹范数的识别方法

稀疏表示分类法利用L1范数保持表示系数的稀疏性，最小二乘回归分类法利用L2范数保持表示系数的聚集性，本文利用迹范数保持表示系数的稀疏性和聚集性。

2.1 正则迹范数模型

为了平衡L1范数和L2范数，文献[8]提出了迹范数Ω（w）=||XDiag（w）||*，不同于其他范数，迹范数包含数据集X，可以自适应保持数据集的相关性，从而更好地保持数据的相关信息。XDiag（w）可以分解为：

文献[8]指出，||w||2≤||XDiag（w）||*≤||w||1，因此，迹范数能同时保持表示系数的稀疏性和聚集性，将Ω（w）=||XDiag（w）||*作为正则项，建立基于迹范数的识别方法：

2.2 模型求解

求解模型正则迹范数模型有许多方法[8-9]，本文利用交替乘子方向法（Alternating Direction Method of Multipliers，ADMM）[11]求解正則迹范数问题。

2.3 正则迹范数分类法

利用训练集X对每个测试样本y求解表示系数w，然后用最近邻子空间准则对测试样本y进行分类，将这一过程归纳为基于正则迹范数的分类法（Trace Norm Regulation Classification Method，TNRC）。

算法二：正则迹范数分类法

输入：训练集X，测试样本y，训练样本类别ltrain，正则参数λ，γ

输出：测试样本类别ltest

第一步：利用迭代方法求解表示系数w;

第二步：利用最近邻子空间准则测试样本y分类，得到测试样本类别ltest。

3 实验分析

本节通过实验验证了正则迹范数分类法（TNRC）可以提高人脸识别的准确率，选用的对比方法包括经典的稀疏表示分类法（SRC）和最小二乘回归分类法（LSRC）、非负最小二乘回归分类法（NNLSC）以及最近邻分类法（KNN），主要对比方法的参数设置：稀疏表示分类法的正则参数和正则迹范数分类法的正则参数λ都设置为0.000 1。

实验数据集为四个常用的人脸图像数据集，分别为FERET，ORL，PIE和Yale，它们的主要信息见表1所列。

3.1 主要实验结果对比

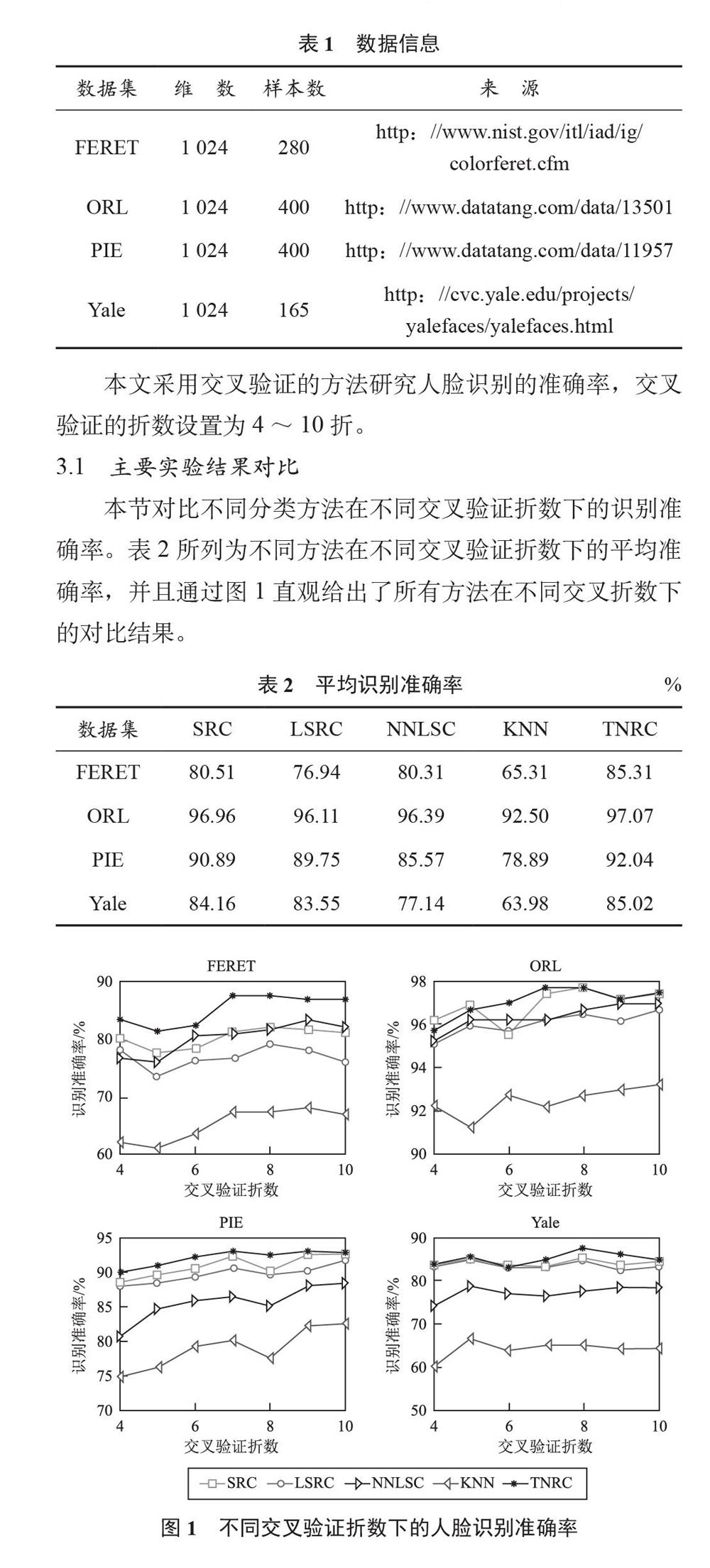
本节对比不同分类方法在不同交叉验证折数下的识别准确率。表2所列为不同方法在不同交叉验证折数下的平均准确率，并且通过图1直观给出了所有方法在不同交叉折数下的对比结果。

从表2的平均识别准确率可以发现，正则迹范数分类法的平均准确率最高，因此本文提出的方法适合人脸图像的识别。不仅如此，从图1的实验结果不难发现，正则迹范数分类法（TNRC）取得了較好的聚类准确率，说明Ω（w）=||XDiag（w）||*很好地保持了稀疏表示分类法的稀疏性和最小二乘回归分类法的聚集性。不难发现，最近邻分类法（KNN）的识别准确率明显低于其他方法，反映了传统分类方法不适合人脸图像数据高维数非线性的特点。

3.2 参数讨论

本节研究正则迹范数分类法（TNRC）的正则参数λ对人脸识别准确率的影响。

从图2的实验结果不难发现，较小的正则参数可以得到更准确的识别准确率。当λ=1时，识别准确率明显下降，因此，在用正则迹范数分类法进行人脸识别时，可以设置较小的正则参数，以提高识别准确率与正则迹范数分类法的实用性。

4 结 语

本文利用迹范数理论提出了正则迹范数分类法，并用该方法研究了人脸识别问题。正则迹范数分类法通过正则迹范数达到保持表示系数的稀疏性和聚集性，提高表示系数的表示能力，从而提高识别准确率。在四个人脸图像数据集上的实验表明了该方法的有效性，但由于该方法利用交替乘子方向法（ADMM）求解，需要较大的时间开销，因此研究正则迹范数模型的快速求解将是一个不错的课题。

参 考 文 献

[1] TURK M，PENTLAND A. Eigenfaces for recognition [J]. Journal of cognitive neuroscience，1991，3（1）：71-86.

[2] TOLBA A S，ELBAZ A H，ELHARBY A.Face recognition：a literature review [J]. International journal of signal processing，2008，2（1）：88-103.

[3]潘周娴，陈适，潘慧，等.人脸识别技术的医学诊断应用的发展与现状[J].基础医学与临床，2016，36（12）：1747-1750.

[4] GAO Y，MA J，YUILLE A L. Semi-supervised sparse representation based classification for face recognition with insufficient labeled samples [J]. IEEE transactions on image processing，2017，26（5）：2545-2560.

[5] WRIGHT J，YANG A Y，GANESH A，et al. Robust face recognition via sparse representation [J]. Pattern analysis and machine intelligence，2009，31（2）： 210-227.

[6] CHEN X，JIAN C. A tumor classification model using least square regression[C]// International Conference on Natural Computation. IEEE，2014：753-758.

[7] LI Y，NGOM A. Classification approach based on non-negative least squares[J]. Neurocomputing，2013，118（11）：41-57.

[8] OBOZINSKI G，BACH F. Trace Lasso： A Trace Norm Regularization for Correlated Designs [C]// International Conference on Neural Information Processing Systems. Curran Associates Inc. 2011：2187-2195.

[9] LU C，FENG J，LIN Z，et al. Correlation adaptive subspace segmentation by trace lasso[C]// IEEE International Conference on Computer Vision. IEEE，2014：1345-1352.

[10] KIM S J，KOH K，LUSTIG M，et al. An interior-point method for large-scale l1-regularized least squares[J].IEEE journal of  selected topics in signal processing，2007，8（8）： 1515-1559.

[11] BOYD S，PARIKH N，CHU E，et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J].Foundations & trends in machine learning，2011，3（1）：1-122.