不均匀沉降架空管道桁架桥的有限元计算分析
2019-08-15思1聪1徐征南1牛琦锋1林冠堂陈英红
黄 思1,张 聪1,徐征南1,牛琦锋1,林冠堂,陈英红
(1.华南理工大学 机械与汽车工程学院,广州 510641;2.广东省特种设备检测研究院 珠海检测院,广东珠海 519002)
0 引言
化工园区的架空管道一般用于输送各种温度、压力和流动工况的化工原料和成品。在基础不均匀沉降地段,立柱、钢架和管道产生相对错位,容易出现结构局部变形,直接影响架空管道的作业安全[1-2]。近年来,因地基不均匀沉降带来的储运设备安全问题引起了有关研究人员的关注。冷建成等[3-5]分别对地基不均匀沉降下的管道做应力分析和沉降变形研究,为管道安全性控制提供一定的理论依据。高红利等[6-8]分别对储罐基础不均匀沉降做受力分析、变形分析及安全性分析,为开展储罐地基沉降安全评估提供技术指导。但缺少有关基础不均匀沉降架空管道的研究报道。
本文选取华南某化工园区一个基础不均匀沉降地段的架空管道桁架桥作为研究对象,采用自动安平水准仪测量架空管道立柱的沉降值,在此基础上考虑重力、介质温度、流动载荷等因素,建立系统完整的ANSYS有限元计算模型进行数值计算,旨在探索一套针对基础不均匀沉降架空管道桁架桥实际应用的安全风险评估方法,为架空管道桁架桥的安全运行提供坚实的技术支持。
1 立柱沉降测量
通过对实际架空管道桁架桥的简化,建立如图1所示的基础不均匀沉降地段架空管道桁架桥几何模型,其纵向和横向具体参数如图2,3所示。

图1 管道桁架桥几何模型
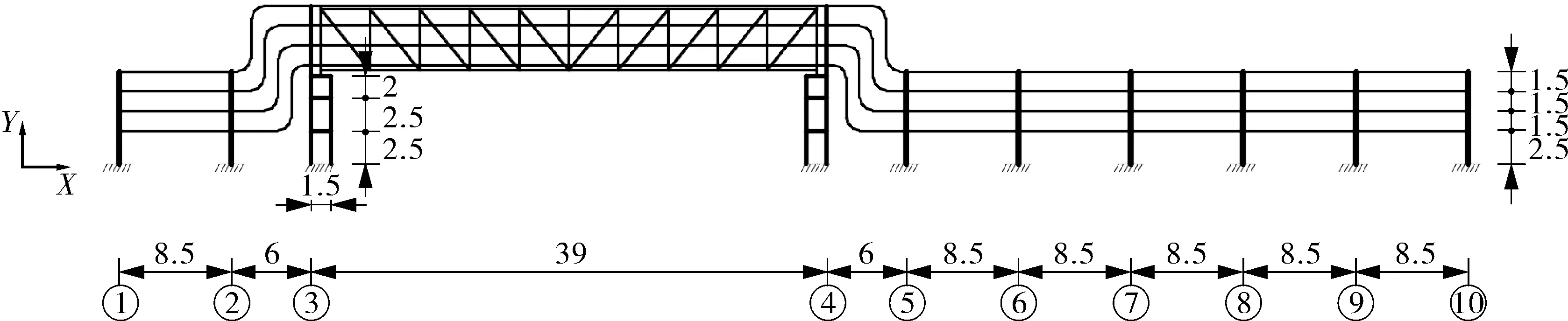
图2 模型纵向示意
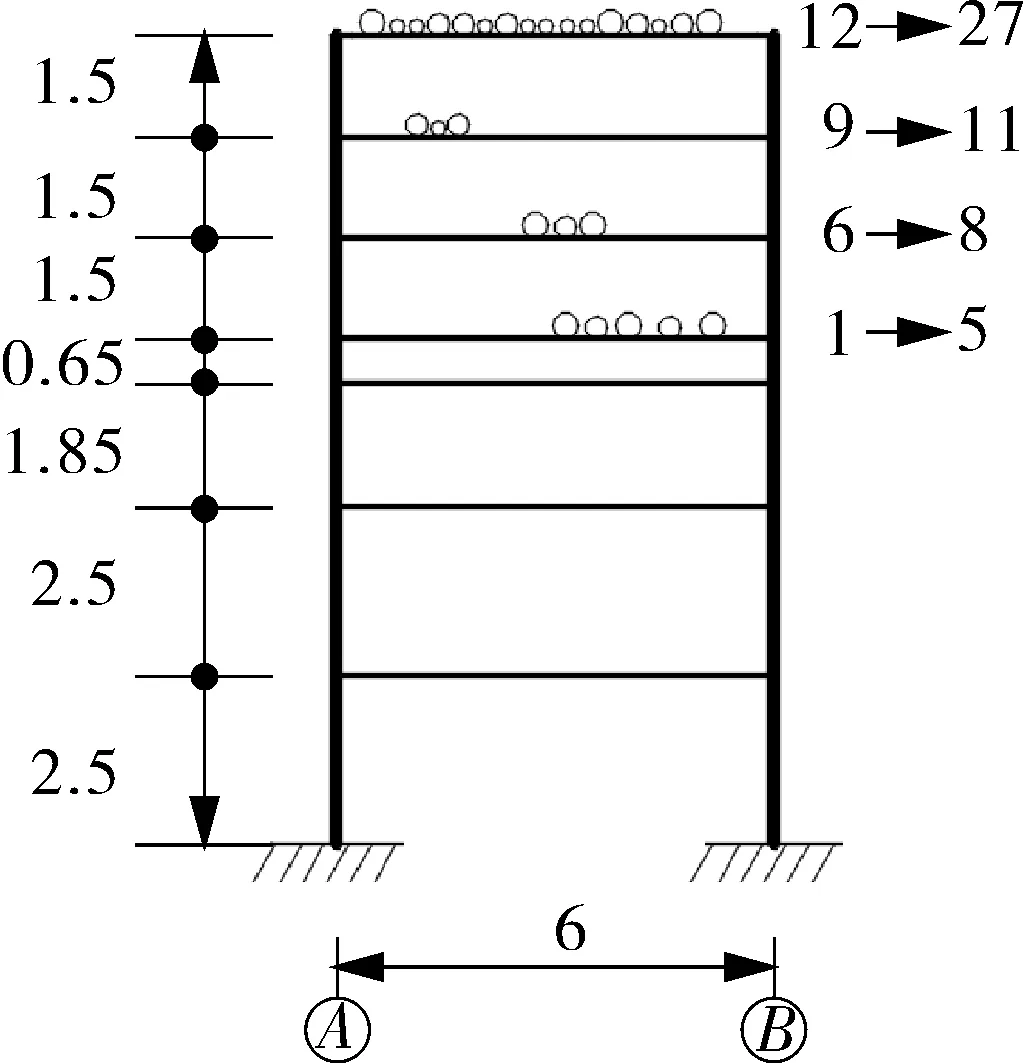
(a)立柱③和④
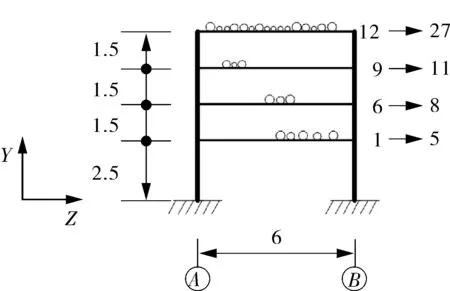
(b)其余立柱
图3 模型横向示意
图4示出最高立柱之间的钢架水平布置图。该系统有10组立柱,4层管架:第1层管架有5根管道;第2层有3根;第3层有3根;第4层有16根,一共27根管道,管道编号如图3所示。
采用可自动视线调平、稳定抗干扰的DSZ3-32X型水准仪测量架空管道立柱的沉降值,得到沉降地段中几组立柱的累积沉降值h如表1所示,其中立柱①和⑩不在沉降地段。
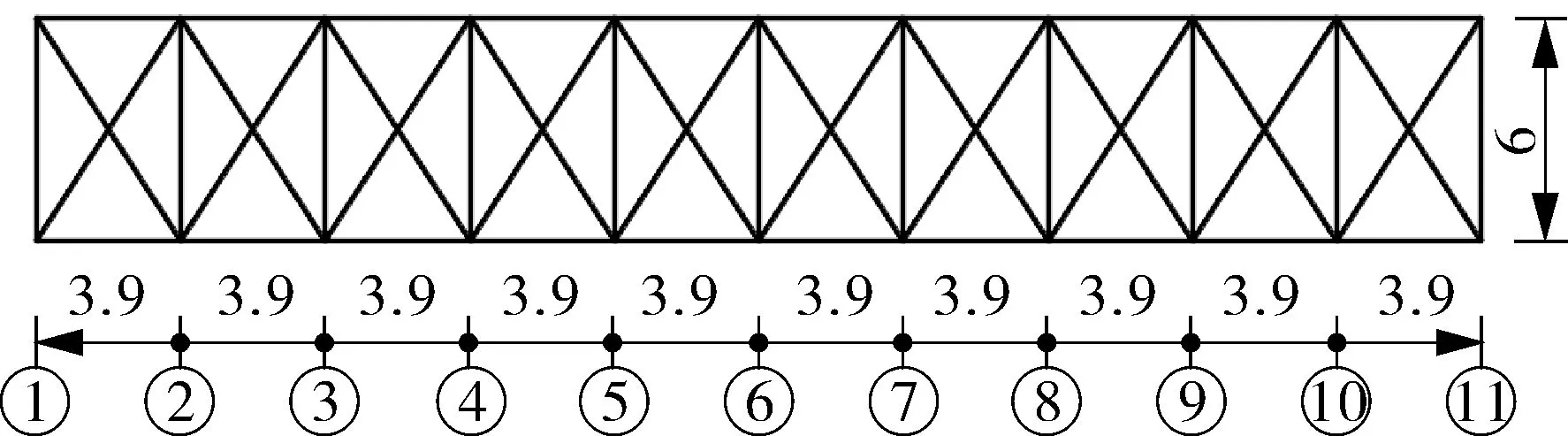
图4 钢架水平布置示意

表1 架空管道立柱累积沉降测量值
2 有限元建模
2.1 计算单元类型
根据图1~4所示的架空管道桁架桥布局,建立ANSYS的APDL有限元计算模型。分别使用梁单元(Beam 189)和管单元(Pipe 289)对管架、钢架和管道进行建模[9-13]。表2列出了管架、钢架和管道单元的具体数据。
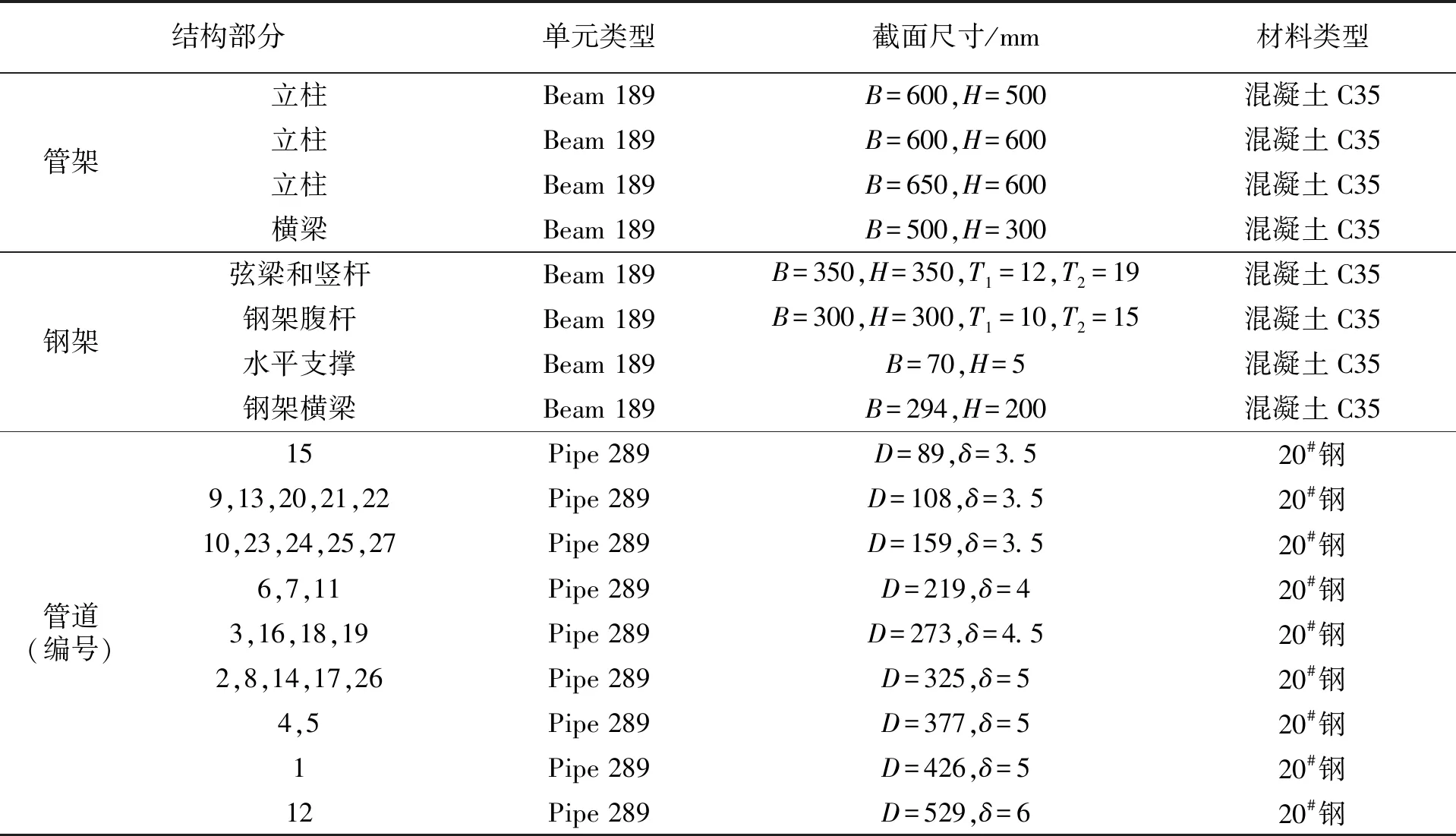
表2 单元参数和材料类型
注:B-梁单元截面长度;H-截面高度;D-管单元外径;δ-管壁厚度;T1-钢架腹板厚度;T2-钢架翼板厚度;单位均为mm
2.2 材料属性
有限元模型中使用的材料常数如表3所示。由结构的材料、单元类型以及单元截面尺寸,建立了完整的架空管道ANSYS计算模型,共包括57 106个单元和28 916个节点。图5为架空管道桁架桥有限元网格模型。

表3 架空管道桁架桥结构材料参数

图5 架空管道桁架桥有限元网格模型
2.3 介质参数
根据现场实际情况,计算所使用的介质种类、操作工况和介质物性参数如表4所示。
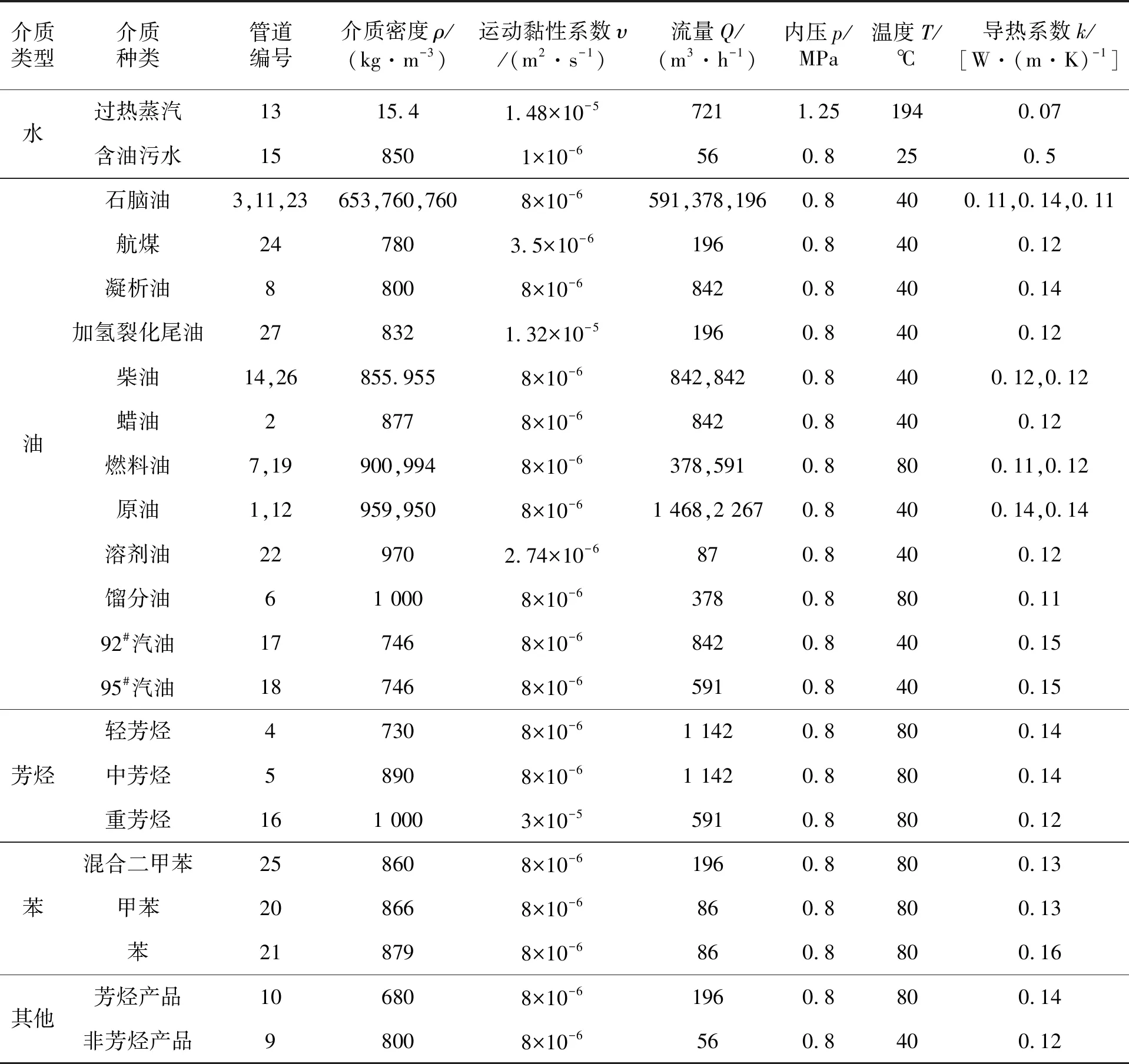
表4 管道输送介质参数
3 载荷与约束条件
载荷主要有重力、介质温度和流动对管道的作用力。计算中对无沉降的立柱底部采取固定约束,有沉降的立柱底部按表1的测量结果设置向下位移[14]。
3.1 介质温度载荷
管道因流动介质温度与安装时环境温度的差异而产生伸缩,故在有限元计算中,需同时考虑温度和结构的选项[15-18]。施加温度载荷时,所需的材料热膨胀系数、介质工作温度和导热系数见表3,4。
3.2 介质流动载荷
流动介质对管道施加的力主要有因黏性流动造成的沿程阻力和因管道变向90°而产生的作用力[19]。
(1)等径管道沿程阻力。
(1)
式中FX——等径管道中流体对管道的作用力,N;
l——管道长度,m;
d——管道内径,m;
v——介质流速,m/s;
A——管道截面积,m2。
沿程阻力系数λ为:
λ=0.3164/Re0.25
(2)
其中:
Re=vd/υ
(3)
式中υ——介质运动黏性系数,m2/s。
作用于等径直管的流体力如图6所示。
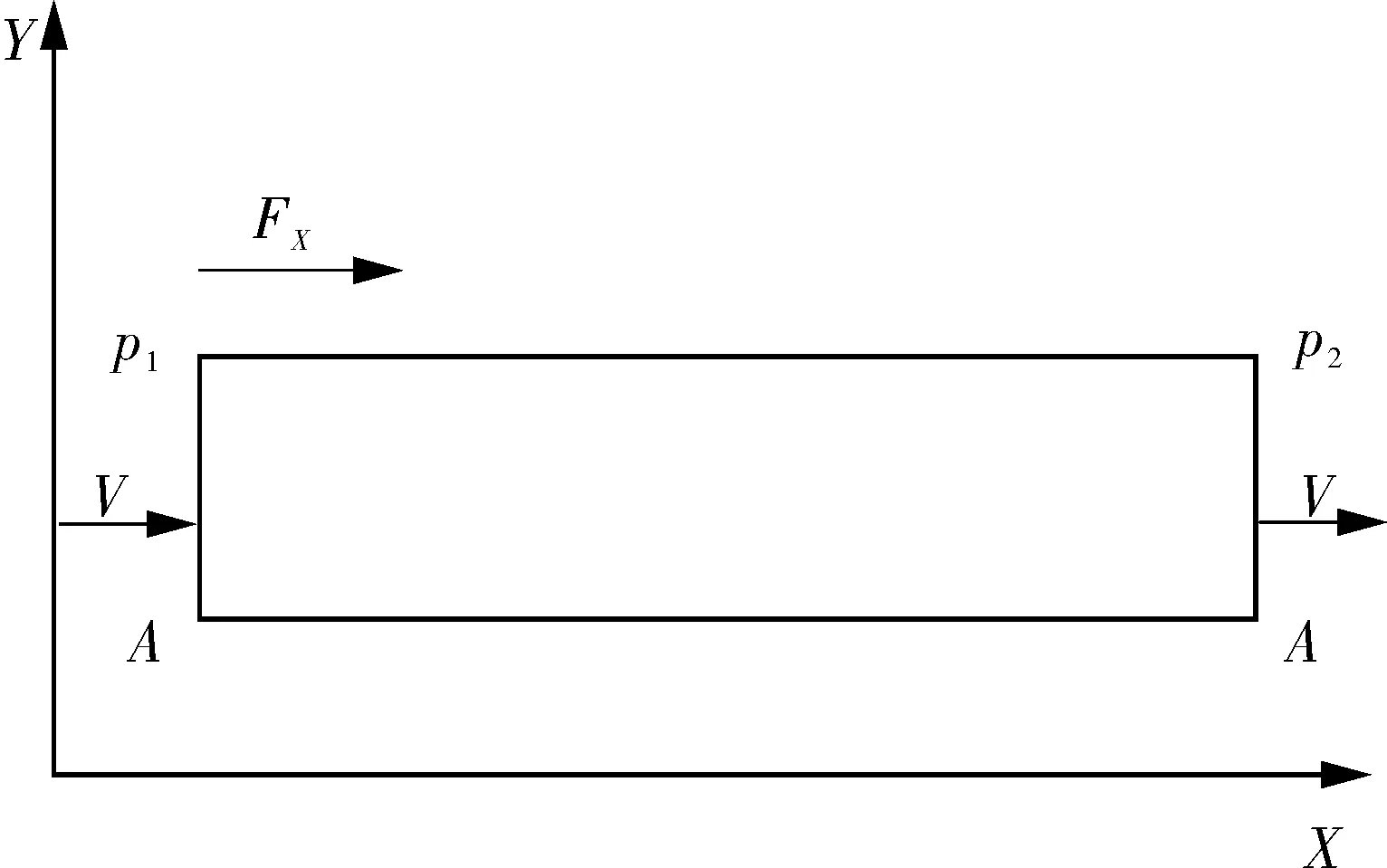
图6 作用于等径直管的流体力
(2)90°等径弯管作用力。
(4)
式中FX——90°等径弯管中流体对管道X向的作用力,N;
FY——90°等径弯管中流体对管道Y向的作用力,N。
作用力方向和作用点如图7所示。

图7 作用于90°等径弯管的流体力
4 计算结果与分析
4.1 位移分布
图8,9分别示出计算得到的架空管道桁架桥X向和Y向位移分布(坐标分别代表架空管道桁架桥X向和Y向位移,正值表明与坐标轴方向一致,负值表明与坐标轴方向相反,单位为m)。可以看出,最大X向位移(15.2 mm)出现在编号26、输送介质为精制柴油的管道,位于管道倒角与管架②横梁接触的地方;最大Y向位移出现如图4钢架水平布置的⑥和⑦之间,最大位移值为17.2 mm。
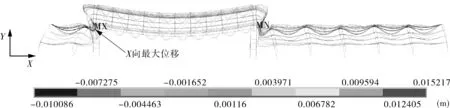
图8 架空管道桁架桥X向位移分布

图9 架空管道桁架桥Y向位移分布
此外,一般结构在静力作用下需要满足δ/L≤1/900(δ表示最大挠度,L表示桁架桥的长度),可以检验该桥在此集中荷载作用下满足刚度要求,即δ/L=0.017224/39=4.42×10-4<1/900=1.11×10-3,可知该结构在综合力作用下满足刚度要求[20]。
4.2 应力分布和强度校核
图10示出计算得到的架空管道桁架桥等效(von Mises)应力分布(坐标代表架空管道桁架桥等效应力,单位为Pa)。可以看出,最大应力(150 MPa)出现在编号9、输送介质为非芳烃产品线的管道与管架②第3层横梁接触的地方。由于该管道内径小、介质温度高、黏度大,所以该管道应力高于其他管道。
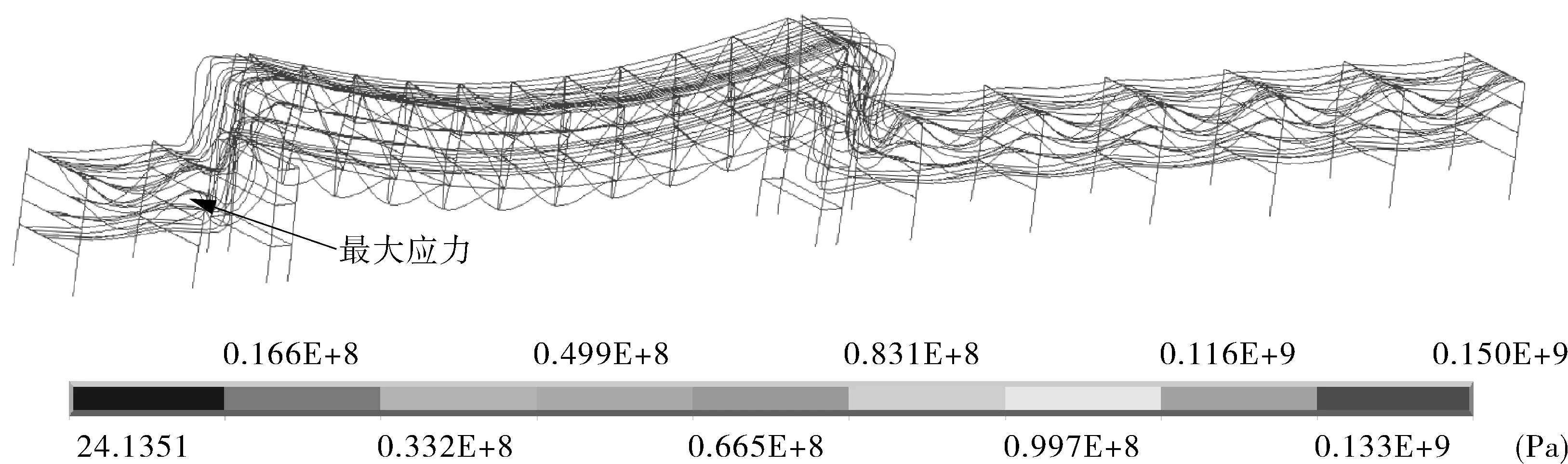
图10 架空管道桁架桥等效应力分布
根据行业的技术规程[21]可知,管材因热胀冷缩和其他位移受到约束而产生的热胀二次应力σf需满足以下条件[22]:
(5)
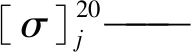

对于架空管道所采用20#钢,按式(5)得知二次应力值应满足σf≤189 MPa。由图10可以看出,计算得到的架空管道桁架桥最大应力为150 MPa,满足条件σf≤189 MPa,故该不均匀沉降地段的架空管道运行可靠。
4.3 临界沉降值
为考察该地段架空管道桁架桥所能承受的临界沉降大小,在计算模型中对各立柱分别单独设置沉降值h(其余立柱无沉降),计算出所对应的系统最大应力σmax,得到如图11所示的单柱沉降值h和最大应力σmax关系,由此可根据管材的许用应力[σ]求出各单柱的临界沉降值hcr。以20#钢的二次许用应力为例,在图11中做σmax=189 MPa的水平线与其余各线相交,得到各交点的横坐标h即为各单柱的临界值hcr,如表5所示。由表5可以看出,最高立柱③④和相邻立柱②⑤所能承受的沉降值较小。

表5 单柱的临界沉降值hcr
5 结论
通过对某化工园区基础不均匀沉降地段的架空管道桁架桥的沉降测量和有限元计算,得到以下结论。
(1)所研究的架空管道桁架桥最大位移出现在钢架中间,通过δ/L的刚度验算,管道桁架桥的刚度满足设计要求。
(2)在整个架空管道桁架桥中,最大应力出现在内径小、介质温度高、黏度大的管道与横梁接触的位置。经强度校核,该不均匀沉降地段的架空管道桁架桥满足应力校核。
(3)不均匀沉降架空管道桁架桥中最高立柱和相邻立柱所能承受的沉降值较小,需重点关注这些立柱的沉降情况。
(4)所采用的热流固耦合有限元计算方法对基础不均匀沉降地段的架空管道受力分析是切实可行的,可为在役架空管道的安全运行提供坚实的技术支持。
