动量守恒定律的解题方法和技巧

戴诚超

(福建省南平第一中学 福建 南平 353000)

1.明确研究对象和过程，合理选择系统

在自然界当中普遍遵循的机械运动规律就是动量守恒定律，这也是考试当中的经典考点，当系统不受外力或受到的外力合力为0或系统内力远大于内力的时候，那么这个系统总动量是守恒的，动量守恒定律表现出了研究对象的整体性以及时间的对应性。动量守恒定律的研究对象不是单个的物体，而是一个系统，所以在解题伊始，我们要选择好系统。例如，在光滑的平面上有三个质量相同的小球，球A与球B通过轻质弹簧连接，球C以初速度v0沿着A、B两球连接的方向向球B运动(如图1)，当与B球碰撞之后就与其结为一体，则求解弹簧压缩量最大时的弹性势能。

图1

当B、C两球发生碰撞时，碰撞时间短且两球的相互作用力远大于外力，B球和C球系统的动量守恒，B球和C球在碰撞之后具有共同的速度v,A球的状态保持不变。

根据动量守恒定律得到mCv0=(mC+mB)v,

那么v=mCv0/(mC+mB)=v0/2

碰撞之后B球和C球为一个整体，以速度v对弹簧进行压缩，A球与B球同时受到弹簧的弹力作用，此时应将球A、B、C和弹簧视为一个系统，动量守恒定律依然适用。当弹簧的压缩量最大时，三个球的共同速度为v′，

根据动量守恒定律得到(mC+mB)v=(mC+mB+mA)v′

那么v′=(mC+mB)v/(mC+mB+mA)=v0/3

根据机械能守恒定律，B球和C球以速度v压缩弹簧直到三个小球的共同速度为v′的过程当中，这个系统所减少的动能转化为弹性势能，

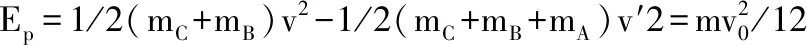
在求解此题的过程中，如果只是盲目地应用动量守恒定律，而没有明确在B、C球碰撞过程中有机械能的损失，很容易就将碰撞和压缩弹簧两个过程合并成一个过程来进行求解，这样虽然求解出来的速度仍然为v0/3，但是最后计算的弹簧的弹性势能却是错误的。

2.对于多过程问题，抓住系统初、末状态进行求解

动量守恒定律的研究对象一般由两个或两个以上的物体组成系统，而且往往会涉及到多过程问题。但是动量守恒定律的优点就在于不需要像牛顿运动定律那样去分析每一个过程，对于初、末状态过程当中系统当中的各个物体相互作用的过程则无需考虑。在对多过程问题运用动量守恒定律进行求解的时候，要对物体运动状态的同时性、动量守恒方程矢量性多加注意，有些题目中还要考虑物体的相对速度，要从统一参考系当中把握动量守恒定律的各个速度。

例如，以木板放置在光滑的水平地面上，左端放置一木块，右侧有竖直墙面，已知木块的质量是木板质量的2倍，木块与木板之间的动摩擦因数为μ，让木板与木块以相同的速度v0向右运动，当木板与墙发生弹性碰撞时，碰撞的时间非常短(如图2)。求木板从第一次与墙发生碰撞到再一次与墙发生碰撞所经历的时间，假设木板足够长，木块的位置始终在木板上，重力加速度为g。

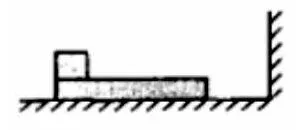
图2

本道例题是一道典型的多过程动量守恒的题目，木板先经过了碰撞反弹，匀减速，匀加速和匀速直线运动这几个过程，如果用牛顿运动定律去求解的话，虽然也能够解出，但是费时费力，要对木板的每一个过程分别列式，步骤繁琐且易错。

当木板与墙壁初次碰撞后，最后木板和物块达到一共同速度，设木板的质量为m，木块的质量为2m，假设水平向右是正方向，那么根据动量守恒定律得到

2mv0-mv0=(2m+m)v,得到v=v0/3,

对木板由动量定理得到μ·2mgt1=mv-m(-v0),

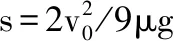
当木板匀速运动的时候，s=vt2,

所以木板与墙的初次碰撞到再次碰撞的时间为t=t1+t2=4v0/3μg

在求解此题的过程中，把与墙壁碰撞后反弹的木板和木块视为一个系统，忽略中间的过程，对初、末状态列出动量守恒式，求出木板和木块的最终速度后再进行求解。

3.重视碰撞和爆炸问题

对于动量守恒定律，就是要处理好碰撞(爆炸)的问题，这也是动量守恒定律中常见的一类问题。在碰撞(爆炸)的过程当中，系统内各个物体之间的相互作用的内力要远大于系统所受的外力，而且作用时间极短，所以我们可以不考虑外力的冲量，将系统的动量视为守恒。碰撞(爆炸)问题往往还都会涉及到能量守恒，所以在碰撞问题当中要分清弹性碰撞和非弹性碰撞，因此，老师们一定要对碰撞的问题进行详细的讲解。碰撞和爆炸问题虽然属于同一类型的考点，但是还是有一些区别的。对于碰撞问题，系统的机械能是不会增加的，而对于爆炸问题，有化学能能转化为系统的机械能，所以系统的机械能会增大。例如一颗手榴弹在5米的高度以10m/s的速度水平飞行时炸裂成质量比为3:2的两个小块，质量稍大的以100m/s的速度反向飞行，问这两小块落地点的距离是多少。