一种去除椒盐噪声的自适应模糊中值滤波算法
2019-08-15万丰丰周国民周晓
万丰丰,周国民,周晓
(1.浙江工业大学信息工程学院,浙江杭州310023;2.浙江警察学院,浙江杭州310053)
椒盐噪声通常来自图像的产生、传输、处理和存储过程[1],主要由图像的极值组成,在视觉上表现为黑白相间的亮暗点,会严重影响图像质量,也给图像的后续分析和处理造成困难。因此,如何有效去除椒盐噪声、保护图像细节具有十分重要的研究意义。
标准中值滤波(SMF)算法[2]是一种非线性滤波方法,对椒盐噪声具有良好的平滑效果,因此,在图像降噪领域得到了广泛的应用。然而,SMF算法采用预设的固定窗口对每个像素点进行相同的处理,不区分噪声点和信号点,在去除噪声的同时容易导致图像细节模糊。为此,提出了各种改进算法。自适应中值滤波(AMF)算法[3-4]可自适应调整滤波窗口的大小,并采用非噪声的中值点代替窗口中心像素点,提高了噪声的去除能力,但中值点很可能取到离窗口中心较远位置的像素点,易导致图像细节丢失。文献[5]提出了一种改进的AMF算法,计算滤波窗口在4个方向上各像素点与中心像素点的灰度差值的和,并利用其绝对值的最小值进行噪声检测,对受噪声污染程度较低的图像具有很好的噪声去除和边缘保持效果。当滤波窗口的污染程度较高时,虽然滤波窗口增大,但仍采用标准中值方法去除噪声,易导致噪声在邻域的扩散。文献[6]采用多级开关进行噪声检测,提出了一种自适应开关中值滤波(ASM)算法,能有效去除高密度噪声,但其图像边缘细节模糊问题尚未解决。文献[7]提出了基于噪声估计的自适应开关型中值滤波算法,利用支持向量回归(SVR)分析估计图像中的噪声比例,并对不同噪声比例的图像启动不同的滤波策略,提高了对高密度噪声的去除能力,但对低密度噪声图像的滤波效果较为一般。文献[8]提出了一种自适应双阈值的中值滤波方法,选取邻域的均值、滤波窗口内4个方向上灰度均值的最大值和最小值作为噪声检测的双阈值,但其仅利用像素点与邻域的灰度差异进行判断,易将非噪声点误判为噪声。文献[9]提出的模糊中值滤波(FMF)算法,采用极值法进行初步的噪声检测,然后利用疑似噪声点与周围像素点的最大绝对灰度差对疑似噪声点是否为噪声做进一步判断,提高了对噪声的识别能力,对受中、低密度噪声污染的图像具有较好的滤波效果。文献[10]提出了一种自适应模糊中值滤波(AFM)算法,能自适应调整滤波窗口大小并自动计算模糊系数,但其定义的模糊系数和模糊变量受窗口内极值点的干扰较大,当图像受噪声污染严重时,滤波性能严重下降。文献[11]设计了一种去除高概率噪声的模糊滤波器,利用滤波窗口非噪声点的模糊划分结果进行模糊估计,由于缺乏合适的窗口自适应机制,当图像噪声密度很高时,模糊划分取到的非噪声点往往离待测像素点较远,它们的灰度相关性较低,致使模糊估计的准确性降低。
借鉴模糊数学和中值滤波思想,本文提出了一种自适应模糊中值滤波(AFMF)算法,并通过与多种算法的对比实验,验证了本文算法的有效性。
1 算法的基本思想及实现
采用先检测后滤波的策略。在噪声检测阶段,采用极值法进行噪声检测,将像素点分为非噪声点(信号点)和疑似噪声点。为判断疑似噪声点是否为噪声,定义了模糊隶属度函数,并对疑似噪声点进行模糊分类。在噪声去除阶段,对于信号点,保持原值输出;对于疑似噪声点,设计了窗口自适应策略,并利用模糊加权的中值滤波器对模糊分类的3种结果进行统一处理。
1.1 噪声检测阶段
用Lsalt和Lpepper表示椒盐噪声的灰度值,通常椒盐噪声表现为图像的极值,在8位灰度图像中Lsalt=255、Lpepper=0。根据椒盐噪声的极值特性,可用极值法进行噪声检测。如果像素点的灰度值等于图像的灰度值极值,则像素点可能是噪声点,将其标记为疑似噪声点;否则,像素点是非噪声点,将其标记为信号点。用X表示受椒盐噪声污染的灰度图像,x(i,j)为图像X中像素点(i,j)的灰度值。定义布尔变量N(i,j),对像素点(i,j)的极值法检测结果进行标记:

疑似噪声点可能是噪声,也可能是图像的极值点,而极值点包含了原始图像的细节信息,对图像后期处理具有重要的价值,因此需对疑似噪声点做进一步判断。
定义滤波窗口W2r+1,其以像素点为中心,大小为(2r+1)(2r+1),Wr+1可表示为

式(2)中r为正整数,x(i,j)表示像素点(i,j)的灰度值。r取值为1时,W3(i,j)代表3×3的滤波窗口,

根据椒盐噪声的极值特性,若像素点(i,j)是孤立噪声点,则它与周围像素点的灰度差别很大。利用这一特点,FMF算法[9]、NAFSM 算法[12]采用疑似噪声点和与其相邻像素点的最大绝对灰度差作为模糊变量,根据模糊变量的大小进一步判断像素点是否为噪声。但该模糊变量存在2个缺陷,一是滤波窗口内疑似噪声点对模糊变量计算结果的干扰较大,因为只要滤波窗口内存在与窗口中心像素点不同的疑似噪声点,模糊变量计算结果就等于255,此时可能将像素点(i,j)误判为噪声,而且噪声密度越大,误判的可能性也越大;二是在较大的滤波窗口内计算模糊变量,可能引入新的偏差,因为模糊变量可能由较远位置的像素点与像素点(i,j)的绝对灰度差得到,而像素间的距离越远,其灰度相关性越低。为避免出现上述问题,本文定义了新的模糊变量。
为解决图像滤波时部分边界像素点无法建立滤波窗口的问题,本文将靠近图像边界的rmax个像素向外翻折以扩充图像边界,即以图像边界为对称轴,向外镜像复制rmax个像素,rmax表示最大滤波窗口的边心距,滤波完成后,裁剪原始图像区域,得到滤波输出图像。该方法可确保图像边界的像素点都能进行滤波处理,且扩充区域保持了与图像边界相似的灰度特性。
图像滤波通常是按照从左至右、从上到下的顺序遍历像素点的。当对像素点(i,j)进行滤波时,W3(i,j)内左上角4个像素点已经过滤波处理。将最小滤波窗口W3(i,j)内左上角4个像素点的灰度值保存到集合S中,如果W3(i,j)左上角4个像素点已经过滤波处理,则将4个像素点滤波后的灰度值更新到集合S中,S可表示为
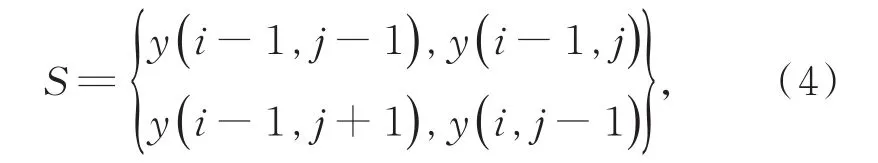
式(4)中,y(i,j)表示像素点(i,j)滤波后的灰度值。
经过滤波处理后像素点的灰度值在理论上更接近原始图像的灰度值,因此,可以认为已处理的像素点都是非噪声点。本文采用疑似噪声点与其最小滤波窗口内已处理的像素点的绝对灰度差的平均值作为模糊变量,则模糊变量D(i,j)可表示为

由于模糊变量用最小滤波窗口内已处理的像素点进行定义,有效避免了滤波窗口内疑似噪声点的干扰以及由于窗口尺寸较大而引入新的偏差。模糊变量D度量了像素点与周围非像素点的平均灰度差别。根据模糊变量D(i,j)的大小,对像素点是否为噪声进行模糊推理:
(2)如果像素点(i,j)为疑似噪声点,而D(i,j)的值很小,说明像素点(i,j)与周围像素点的灰度差别很小,则像素点(i,j)很可能是真实像素点,无须进行滤波。
(3)如果像素点(i,j)为疑似噪声点,而D(i,j)的值不是很大,则像素点(i,j)可能为噪声点,也可能为真实像素点。
对于推理(3)中,难以判断像素点(i,j)是否为噪声的情况。基于图像的分片光滑性,像素点(i,j)为噪声的可能性与D(i,j)的大小正相关,即D(i,j)值越大,(i,j)为噪声的可能性越大,可用单调递增的一次函数进行拟合。
根据以上模糊推理,定义判断像素点(i,j)是否为噪声的模糊隶属度函数为
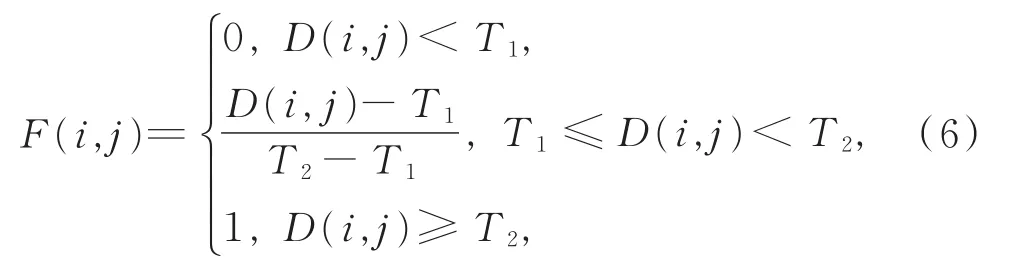
式(6)中,T1和 T2分别表示 D()的低阈值和高阈值。
1.2 噪声去除阶段
当图像的噪声密度大于50%时,滤波窗口内可能一半以上的像素点都是疑似噪声点,SMF算法的处理结果很可能为噪声。窗口内的疑似噪声点会严重干扰中值滤波结果,而信号点是未受噪声污染的像素点,保持了窗口的原始灰度特征。本文利用滤波窗口内信号点的灰度值中值逼近窗口中心像素点的灰度值来避免疑似噪声点对中值滤波结果的干扰。
用变量M(i,j)表示滤波窗口W2r+1(i,j)内所有信号点的灰度值中值,可表示为
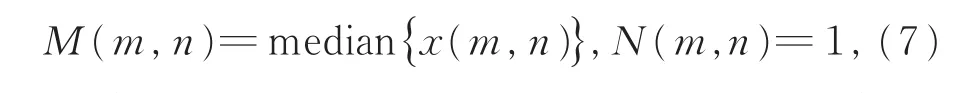
当噪声密度较大时,较小的滤波窗口内可能不存在信号点,此时无法计算M(),因此需增大滤波窗口以确保当前滤波窗口内存在信号点。由变量G2r+1()统计当前滤波窗口W2r+1()中信号点的个数,G2r+1(i,j)可表示为

若采用较小的滤波窗口进行滤波,滤波窗口内可能不存在信号点,若为使滤波窗口内存在信号点而采用很大的窗口进行滤波,算法将变复杂,而且会将离窗口中心较远的信号点引入滤波过程,造成新的偏差,因为较远位置的像素点与窗口中心像素点的灰度相关性较低。为此,本文将滤波窗口的最大尺寸设定为7×7,并设计了窗口自适应策略。对于像素点(),统计其3×3的滤波窗口W3(i,j)内信号点的个数,若G3(i,j)< 1,说明W3(i,j)内不存在信号点,则扩大滤波窗口,令r=r+1;若G2r+1(i,j)<1,则继续增大滤波窗口,直到滤波窗口内存在信号点或者滤波窗口超过预设的最大尺寸。采用这种窗口自适应策略,可确保在尽可能小的滤波窗口得到中值M()的计算结果,有利于保护图像细节。
当滤波窗口调整到合适的尺寸且滤波窗口内存在信号点时,用模糊隶属度函数F(i,j)对滤波窗口内信号点的灰度值中值M(i,j)和当前像素点的灰度值x(i,j)进行加权,得到加权的中值滤波器,利用该滤波器对疑似噪声点的3种分类结果进行统一处理,则像素点(i,j)滤波后的灰度值y(i,j)可表示为

若滤波窗口达到预设的最大尺寸7×7,且G7(i,j)<1,则说明最大滤波窗口内不存在信号点,无法计算M(i,j)。采用最小滤波窗口内已处理的4个像素点的灰度均值替换当前像素点(i,j)的灰度值,用ymean表示最小滤波窗口内已处理的4个像素点的灰度均值:
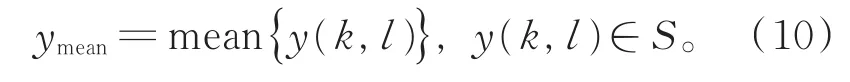
如果滤波窗口达到预设的最大尺寸且仍不存在信号点,则无法计算M(i,j),此时,取窗口内所有像素点的灰度值中值或均值进行滤波均无法有效去除椒盐噪声。已处理的像素点在理论上都是非噪声点,且相邻的像素点间具有一定的灰度相似性,因此,本文采用相邻的已处理的像素点对当前像素点(i,j)进行恢复。
1.3 算法实现
用X表示加入噪声的待测灰度图像,Y表示滤波后的图像。x(i,j)、y(i,j)分别表示图像X和图像Y中对应像素点(i,j)的灰度值。用W2r+1(i,j)表示像素点(i,j)的滤波窗口,其最小滤波窗口为3×3,最大滤波窗口为7× 7,即rmax=3。
本文AFMF算法的实现步骤如下:
(1)输入测试图像X。
(2)采用极值法对像素点(i,j)进行噪声检测,若N(i,j)=0,则像素点(i,j)为疑似噪声点,执行步骤(3);否则,像素点为信号点,保持原值输出,即y(i,j)=x(i,j)。
(3)以像素点(i,j)为中心建立3×3的滤波窗口W3(i,j),并将W3(i,j)左上角4个像素点的灰度值保存到集合S中,如果这4个像素点已经过滤波处理,则将4个像素点滤波后的灰度值更新到S中。 然后按式(5)和式(6)计算模糊变量D(i,j)和模糊隶属度函数F(i,j),若像素点被判断为非噪声点,则保持原值输出,即y(i,j)=x(i,j);否则,执行步骤(4),进入滤波阶段。
(4)统计当前滤波窗口W2r+1(i,j)内信号点的数量,若G2r+1(i,j)≥1,说明当前滤波窗口内存在信号点,执行步骤(5);否则,滤波窗口内不存在信号点,则增大滤波窗口,令r=r+1,然后判断当前滤波窗口是否超过预设的最大尺寸,若r≤rmax,则重复步骤(4);否则,说明最大滤波窗口内也不存在信号点,则执行步骤(6)。
(5)按式(7)计算当前滤波窗口内所有信号点的灰度值中值M(i,j),然后按式(9)计算像素点(i,j)的滤波估计值,即y(i,j)=(1-F(i,j))x(i,j)+F(i,j)M(i,j)。
(6)按式(10)计算与像素点(i,j)相邻的4个已处理的像素点的灰度值均值ymean,并用ymean替换当前像素点的灰度值,即y(i,j)=ymean。
(7)若图像遍历完成,则输出滤波后的图像Y;否则,将当前像素点滤波后的灰度值y(i,j)保存到图像Y中,向右滑动滤波窗口,执行步骤(2),进行下一像素的滤波。
2 实验结果与分析
选取大小为512×512的Lena、Goldhill和Peppers图像的8位灰度图像作为实验对象,比较SMF 算 法[2]、AMF 算 法[4]、FMF 算 法[9]以 及 本 文AFMF算法的滤波性能。SMF算法的窗口大小设为5×5,FMF算法的窗口大小设为7×7,AMF算法的最大窗口尺寸设为7×7,本文AFMF算法的最大滤波窗口设为7×7。实验环境为Windows 7操作系统,CPU为Intel Core(TM)i7-3630QM,内存为4 GB,仿真环境为Matlab R2015b。仿真实验用的测试图像如图1所示。

图1 仿真实验用图Fig.1 Test images of simulation experiment
为比较不同算法的滤波效果,采用归一化均方误差(NMSE)、峰值信噪比(PSNR)和结构相似性(SSIM)[13-14]作为度量各算法滤波性能的评价指标。PSNR和SSIM值越大,NMSE值越小,则滤波效果越好。NMSE、PSNR和SSIM的定义如下:
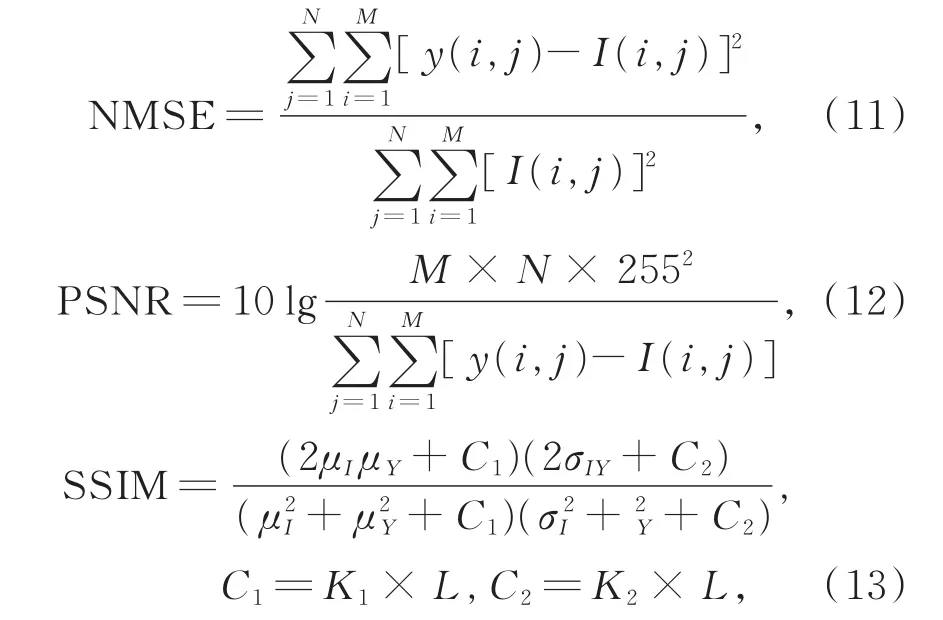
式(11)~(13)中,I(i,j)和 y(i,j)分别表示原始图像I和滤波输出图像Y对应像素点的灰度值,M和N分别表示图像的长和宽。μI,μY分别表示图像I,Y的均值,σI,σY分别表示图像 I,Y 的标准差,σIY表示图像 I,Y的协方差,参数 K1=0.01,K2=0.03,L=255。
为探究参数T1,T2对滤波效果和选取合适参数的影响,等间隔选取参数T1,T2,然后分别对噪声密度为20%,50%,80%的Lena图像进行滤波处理,记录滤波后的PSNR值,如表1所示。

表1 不同T1,T2条件下Lena图像去噪后的PSNR值Table 1 The values of PSNR of the denoised images“Lena”with differentT1andT2
表1中T1,T2的间隔为20,由于T2是判断像素点是否为噪声的关键参数,对滤波结果的影响较大,因此T1和T2间隔大小对滤波结果的影响暂不考虑。 当T2取值为25~35时,滤波后的图像均取得了较高的PSNR值,说明此时滤波效果较好;继续增大T2,PSNR值明显减小,说明滤波效果减弱。当T1=10,T2=30时,算法对不同噪声密度的Lena图像均具有较好的滤波效果,因此本文选取参数T1=10,T2=30。
为定性分析上述算法对不同密度噪声图像的处理效果,利用Matlab中以“salt&pepper”为参数的Imnoise函数[15],给图 1中的 3幅 8位灰度图像分别添加噪声概率为0.2,0.5,0.8的椒盐噪声,生成噪声图像。噪声图像和各算法滤波后的图像如图2~图4所示。

图2 不同算法对受20%椒盐噪声污染的图像的滤波结果Fig.2 Filtering results of different algorithms on images corrupted by 20%salt and pepper noise

图3 不同算法对受50%椒盐噪声污染的图像的滤波结果Fig.3 Filtering results of different algorithms on images corrupted by 50%salt and pepper noise
从图2中可以看出,在20%噪声条件下,几种算法都表现出较好的噪声去除和细节保护效果,本文的AFMF算法滤波后的图像更清晰。从图3中可以看出,在50%噪声条件下,SMF算法滤波后的图像(b)、(g)、(l)中依然存在较多的噪声点,AMF 算法、FMF算法以及AFMF算法滤波后的图像均很清晰。说明在中等密度噪声条件下,SMF算法滤波效果急剧下降,AMF算法、FMF算法以及本文AFMF算法均具稳定的噪声去除和细节保护能力。从图4中可以看出,在80%噪声条件下,SMF算法滤波后的图像十分模糊,AMF算法和FMF算法滤波后的图像也存在大量的“斑点”状噪声,而本文的AFMF算法滤波后的图像比较清晰,从Lena图像中人物的眼睛和帽檐、Goldhill图像中房屋和门窗轮廓以及Peppers图像中青椒边缘轮廓的清晰度可以看出,本文AFMF算法在噪声去除和细节保护等方面明显优于其他3种算法。

图4 不同算法对受80%椒盐噪声污染的图像的滤波结果Fig.4 Filtering results of images corrupted by 80%salt and pepper noise by different algorithms
为定量分析上述算法的滤波性能,给3幅图像分别加入10%~90%的椒盐噪声,然后用上述算法分别对其进行处理。表2~表4分别显示了3幅图像去噪后的PSNR、NMSE和SSIM值。
从表2~表4的数据可以看出:10%~90%噪声范围内,AFMF算法取得了更高的PSNR和SSIM值,以及更低的NMSE值,说明该算法的滤波性能更好。从各项指标的变化情况看,当噪声密度梯度增加时,SMF算法、AMF算法以及FMF算法的性能指标变化剧烈,说明其滤波性能明显下降,而AFMF算法3项指标的数值变化较为平缓,且在90%噪声条件下依然具有较好的性能指标,说明本文算法对不同密度的椒盐噪声具有稳定的去除能力。
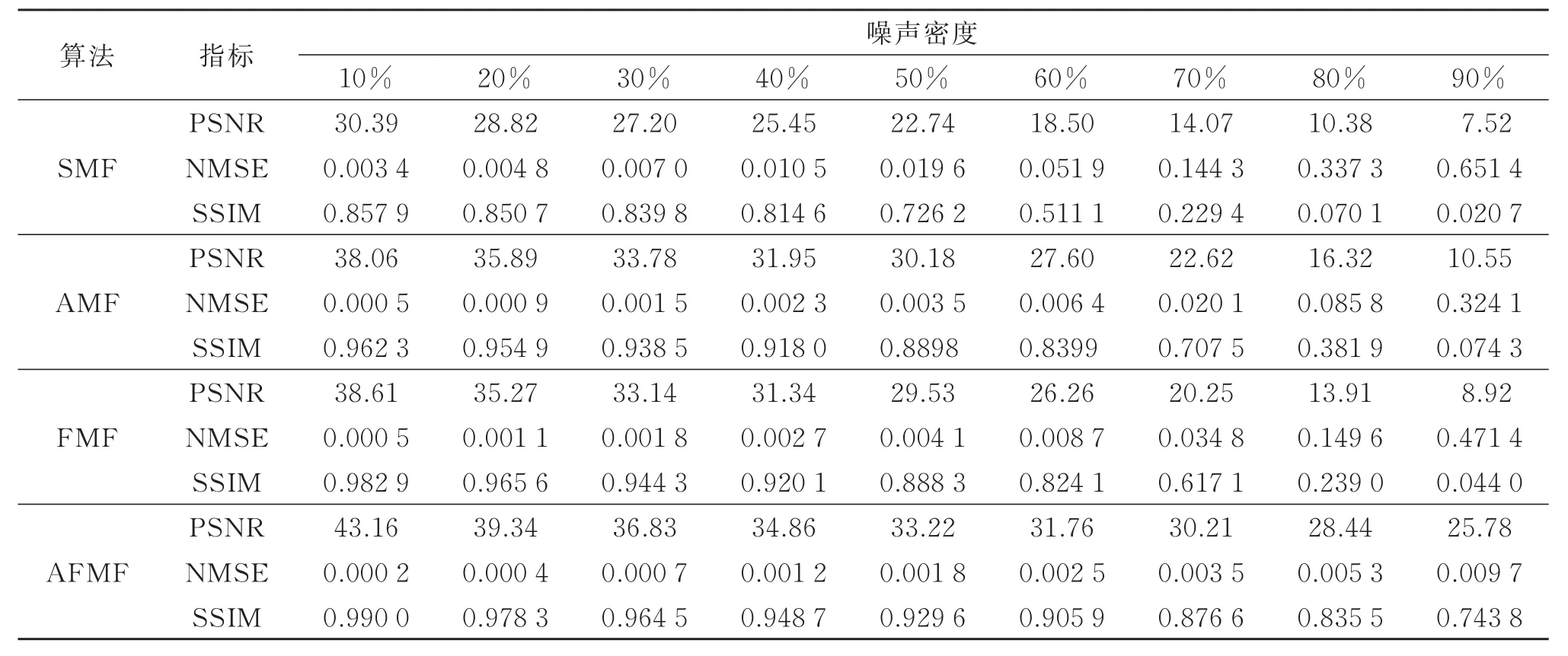
表2 Lena图像去噪后的PSNR、NMSE和SSIM比较Table 2 Comparisons on PSNR,NMSE and SSIM of the denoised images“Lena”
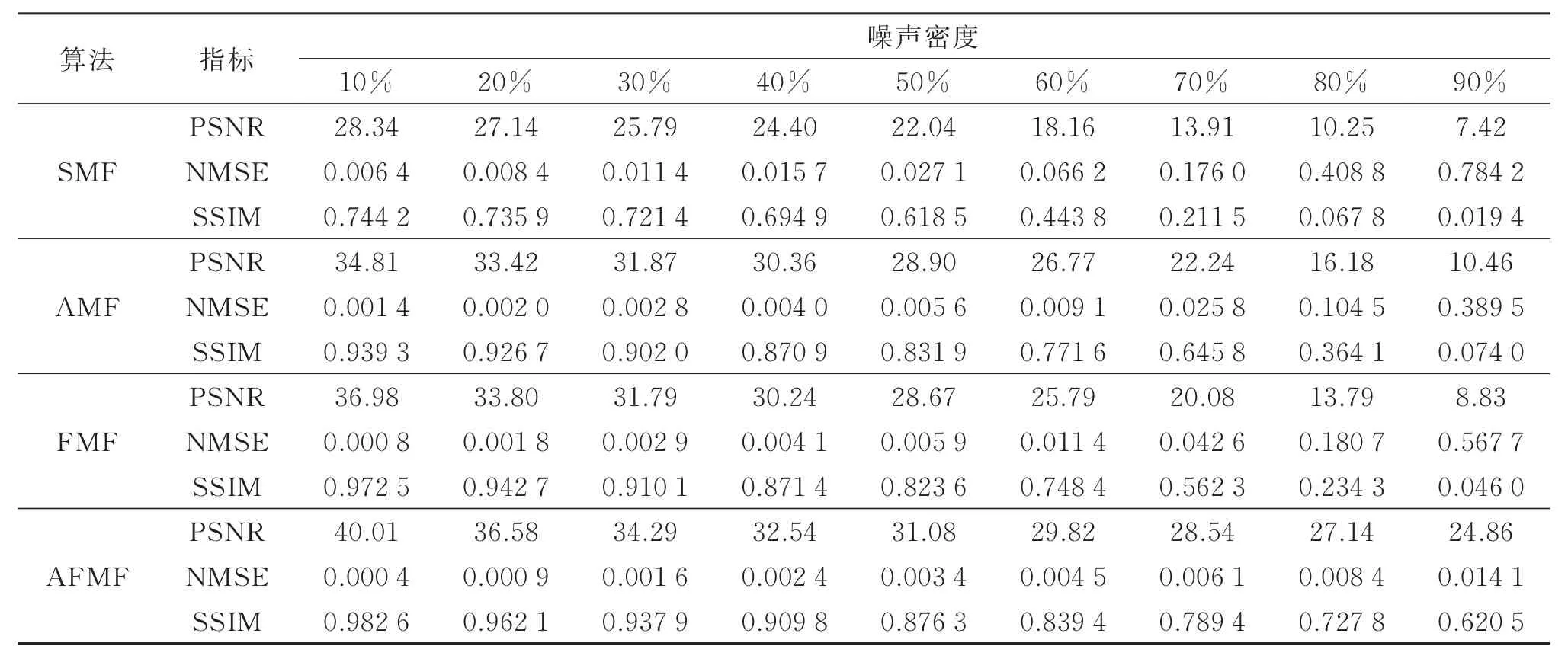
表3 Goldhill图像去噪后的PSNR、NMSE和SSIM比较Table 3 Comparisons on PSNR,NMSE and SSIM of the denoised images“Goldhill”
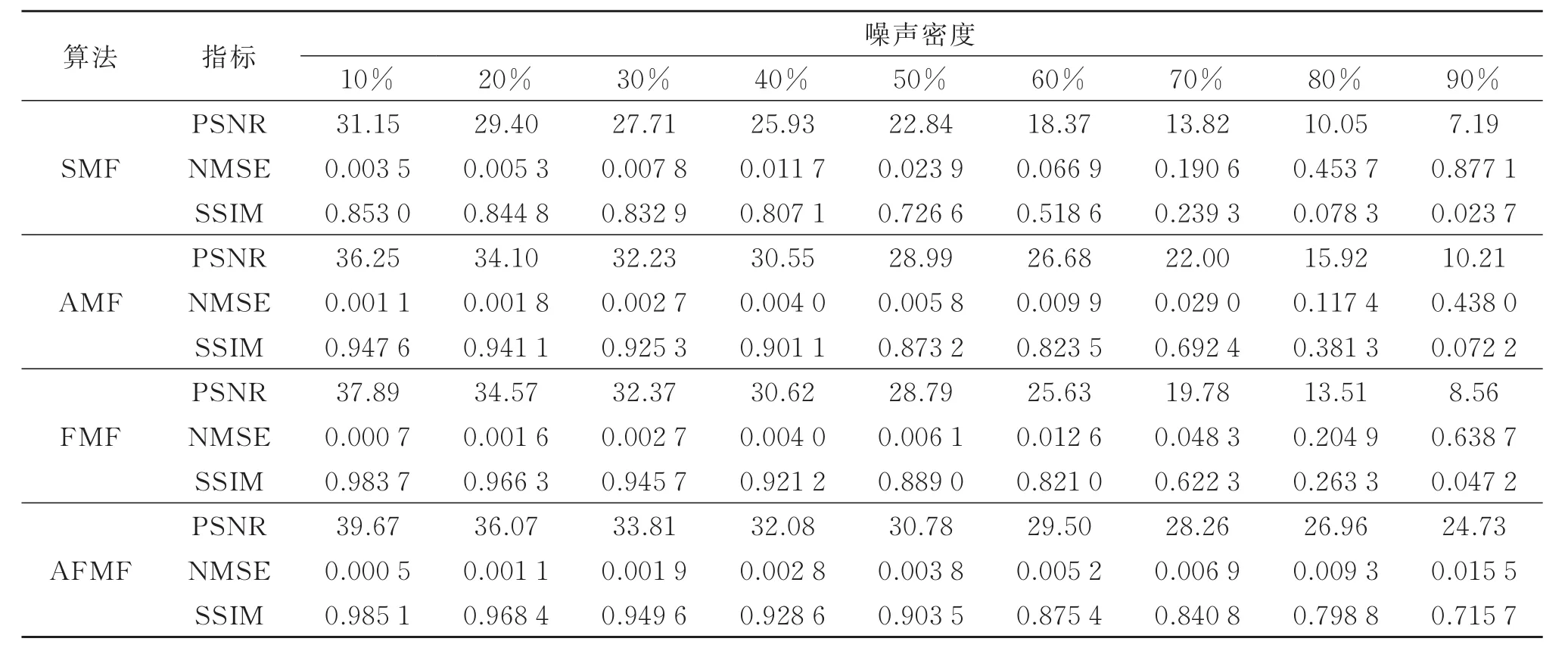
表4 Peppers图像去噪后的PSNR、NMSE和SSIM比较Table 4 Comparisons on PSNR,NMSE and SSIM of the denoised images“Peppers”
3 结 论
针对传统中值滤波方法存在降噪性能不佳以及易导致图像细节模糊的问题,提出了一种自适应模糊中值滤波算法。从3个方面对其进行了优化:一是针对极值法的不足,定义了新的模糊隶属度函数对疑似噪声点做二次检测;二是设计了窗口自适应策略,采用尽可能小的窗口进行滤波,更好地保护了图像细节;三是在噪声去除阶段,滤波器采用滤波窗口内信号点的灰度值中值和待测像素点的灰度值作为加权对象,排除了滤波窗口内疑似噪声点对中值滤波结果的干扰。仿真结果表明,相校于SMF、AMF和FMF算法,本文AFMF算法具有更强的噪声去除和细节保护能力。但也存在一些不足,如算法的复杂度较高、模糊隶属度函数的2个阈值无法自适应获取等。
