保参数方向的形状可调过渡曲线与曲面
2019-08-15李军成李兵易叶青
李军成,李兵,易叶青
(1.湖南人文科技学院数学与金融学院,湖南娄底417000;2.四川航天技术研究院总体部,四川成都610100;3.湖南人文科技学院信息学院,湖南娄底417000)
0 引 言
在许多实际工程问题中,往往需要将2条曲线或2张曲面光滑地连接起来。因此,过渡曲线曲面的构造一直都是重要的研究课题。
为了满足一些特定场合的应用需求,李凌丰等[1]、高晖等[2]、李军成等[3-4]研究了基于势函数与Metaball技术的过渡曲线构造方法;刘华勇等[5-7]与李军成等[8]则讨论了利用调配函数构造过渡曲线的方法。由于应用场合的特殊性,文献[1-8]所构造的过渡曲线与2被过渡曲线的参数方向不一致,过渡曲线在两端点处也只能满足拟连续性。MEEK等[9]、SZILVASI-NAGY 等[10]、HARTMANN[11]采用混合方法构造了保参数方向的过渡曲线曲面,这些方法虽然考虑了2被过渡曲线曲面的全局几何信息,使得构造的过渡曲线曲面更加有效,但无法调整过渡曲线曲面的形状。然而,在一些实际应用场合,常常需要构造既能保持参数方向又能令形状具有可调性的过渡曲线曲面。针对这一问题,李重等[12]提出了一种构造过渡曲线曲面的混合方法,虽然该法不仅可以推广得到任意参数连续或几何连续的过渡曲线曲面,还可通过调节参数获得合适的过渡曲线曲面,但所构造的过渡曲线曲面含有较多的自由参数,确定这些自由参数的计算量较大。江卯等[13]提出的方法可使过渡曲线与2被过渡曲线的参数方向保持一致,还可通过平衡因子对过渡曲线的形状进行调节,但需要事先构造2条辅助延拓曲线。
为了构造保参数方向的形状可调过渡曲线曲面,基于2类带1个自由参数的调配函数,分别构造了满足C1与C2连续的过渡曲线与曲面,其对2被过渡曲线曲面的种类无限制,不仅与2被过渡曲线曲面保持相同的参数方向,而且当2被过渡曲线曲面保持不变时,可通过所含的自由参数调节过渡曲线曲面的形状。通过确定自由参数的取值,还可获得尽可能光顺的过渡曲线与曲面。
1 问题的描述
设Ci(t)(i=1,2)为平面上任意2条参数曲线,且其参数方向相同,如图1所示,希望构造1条从点C1(1)过渡到点C2(0)的参数曲线G(t),并要求:
(1)过渡曲线G(t)的参数方向与被过渡曲线Ci(t)=1,2)保持一致。
(2)过渡曲线G(t)在2个过渡点处满足一定的连续性。
(3)过渡曲线G(t)具有形状可调性。
类似地,给定任意2张参数方向相同的参数曲面Si(u,)(=1,2),如图2所示,希望构造1张从曲线S1(u,1)过渡到曲线S2(u,0)的参数曲面G(u,),并要求:
注1 本文仅考虑过渡曲面与2张被过渡曲面在参数v方向保持一致的情形,在参数u方向保持一致的情形可类似讨论。
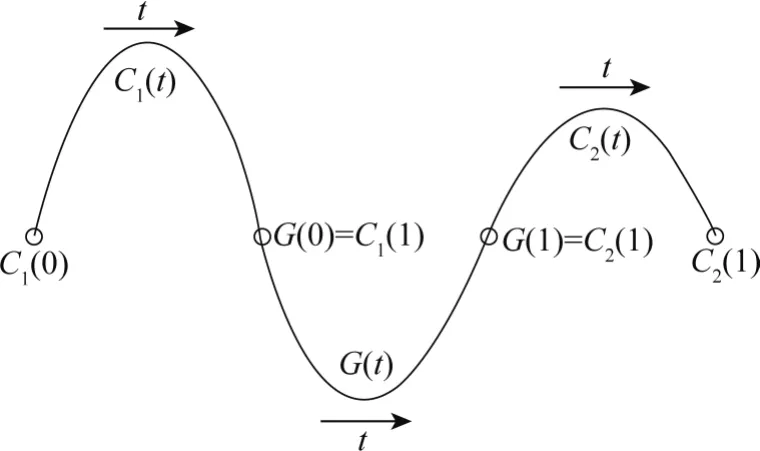
图1 保参数方向构造过渡曲线Fig.1 Constructing transition curve with parameter direction preserving

图2 保参数方向构造过渡曲面Fig.2 Constructing transition surface with parameter direction preserving
注2 需要说明的是,虽然本文讨论的问题是2被过渡曲线曲面取为任意参数曲线曲面的情形,但对于2被过渡曲线曲面为代数曲线曲面的情形也可按此讨论,只要将2被过渡曲线曲面的方程转化为参数形式即可。 例如,当被过渡曲线的方程为y=f(x)(a≤x≤b)时,可将该方程转化为参数形式


为了构造保参数方向的形状可调过渡曲线与曲面,首先给出2类带参数的调配函数:
(1)对于 0≤ t≤ 1,-3≤ α1≤ 12,称关于 t的函数

为第一类带参数α1的调配函数,简称为第一类调配函数。
(2)对于 0≤ t≤ 1,-10/3≤ α2≤ 20,称关于 t的函数[8]

为第二类带参数α2的调配函数,简称为第二类调配函数。
注3 文献[8]利用一种带参数的曲线模型构造出式(2)表示的第二类调配函数,该调配函数可令形状调配问题中的过渡曲线曲面满足C2连续。为了后续构造满足C1连续的过渡曲线曲面,本文利用文献[8]的方法构造了式(1)表示的第一类调配函数,限于篇幅,具体构造过程不再赘述。
不难验证,由式(1)表示的调配函数H1(t)在端点处满足

由式(2)表示的调配函数H2(t)在端点处满足

2 过渡曲线的构造
对于图1所描述的问题,可分别利用式(1)与式(2)表示的调配函数H1(t)与H2(t)构造2类过渡曲线。
定义1 给定平面上2条参数方向相同的被过渡曲线Ci(t)(i=1,2),称曲线
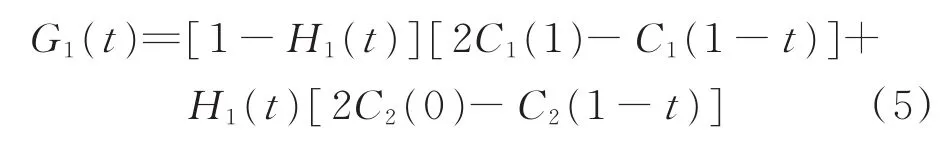
为第一类过渡曲线,其中H1(t)为式(1)表示的第一类调配函数。
定义2 给定平面上2条参数方向相同的被过渡曲线Ci(t)(i=1,2),称曲线

为第二类过渡曲线,其中H2(t)为式(2)表示的第二类调配函数。
定理1 由式(5)与式(6)表示的第2类过渡曲线具有以下特性:
(1)保参数方向性:过渡曲线Gi(t)(i=1,2)与被过渡曲线Ci(t)(i=1,2)的参数方向保持一致。
(2)连续性:过渡曲线G1(t)在2个过渡点处满足C1连续,过渡曲线G2(t)在2个过渡点处满足C2连续。
(3)形状可调性:当被过渡曲线Ci(t)(i=1,2)保持不变时,可通过修改参数α1与α2的取值对过渡曲线Gi(t)(i=1,2)的形状进行调节。
证明由式(3)与式(5)可得

式(7)表明,过渡曲线G1(t)与2条被过渡曲线Ci(t)(i=1,2)的参数方向保持一致,且在2个过渡点处满足C1连续。
由式(4)与式(6)可得
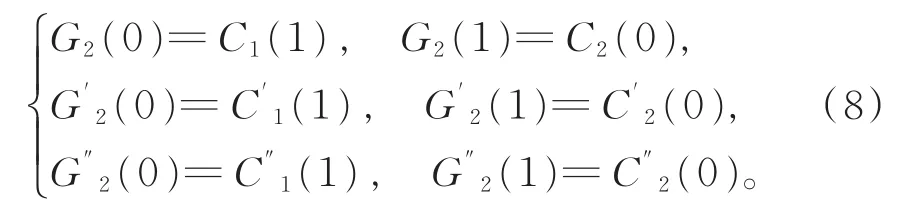
式(8)表明,过渡曲线G2(t)与2条被过渡曲线Ci(t)(=1,2)的参数方向保持一致,且在2个过渡点处满足C2连续。
由于调配函数H1(t)与H2(t)分别带有参数α1与 α2,故由式(5)与式(6)可知,当 2条被过渡曲线Ci(t)(=1,2)保持不变时,可分别通过修改参数α1与α2的取值调节过渡曲线Gi(t)(i=1,2)的形状。证毕。
下面给出2种情形下,保参数方向构造形状可调的C1与C2连续过渡曲线实例。
例1(圆弧间的过渡曲线) 设两圆弧的方程分别为

式中,0≤t≤1。 当参数α1与α2分别取不同值时,C1(t)与C2(t)间形状不同的C1与C2连续过渡曲线如图3所示。

图3 圆弧间的过渡曲线Fig.3 The transition curves between arcs
例2(Bézier曲 线 间 的 过渡曲线) 设 三 次Bézier曲线的方程为

二次Bézier曲线的方程为

当参数 α1与 α2分别取不同值时,C1(t)与 C2(t)间形状不同的C1与C2连续过渡曲线如图4所示。

图4 Bézier曲线间的过渡曲线Fig.4 The transition curves between Bézier curves
注4 由图3与图4可知,当被过渡曲线Ci(t)(i=1 2)保持固定时,所构造的保参数方向过渡曲线在满足C1或C2连续的情形下,可通过参数α1或α2对其形状进行有效调节。但也注意到,参数α2对C2连续过渡曲线的形状调整较为敏感,故在实际应用中要根据具体情况选取合适的参数值。
上述2个实例也表明,当参数α1或α2的取值不恰当时,所构造的C1或C2连续过渡曲线会出现不光顺的情况。 例如,图3中α1=12时的C1连续过渡曲线与α2=-10/3时的C2连续过渡曲线,图4中α2=10时的C2连续过渡曲线。另外,在某些特定的应用场合中,有时也只需确定一条尽可能光顺的过渡曲线。为此,下面给出一种确定参数α1与α2取值的方法,以使得构造的C1与C2连续过渡曲线尽可能光顺。
若记

则式(5)可改写为

根据光顺准则[14],过渡曲线G1(t)的光顺程度可近似地由其能量值来刻画。 能量值Ec1越小,表明过渡曲线G1(t)越光顺。由于式(9)中带有参数 α1(-3≤ α1≤ 12),当 2条被过渡曲线Ci(t)(i=1,2)保持固定时,要使过渡曲线G1(t)尽可能地光顺,只需确定参数α1的取值,使其能量值Ec1尽可能小,即可得优化模型:

则带参数α2的使得C2连续过渡曲线G2(t)尽可能光顺的优化模型为

式(11)与式(12)均为二次函数的条件最值问题,易求得参数α1与α2的值,再分别由式(5)与式(6)即可获得尽可能光顺的C1与C2连续过渡曲线。
注5 当给定的2条被过渡曲线Ci(t)(i=1,2)不可积时,式(11)与式(12)中对应的常数Ai与Bi(i=1,2,3)将无法直接通过计算获得精确值,此时,可利用数值积分公式(如Simpson公式)计算其近似值。
例3 对于例1中给定的2条圆弧,通过求解式(11) 与 式 (12) 可 得 参 数 α1=2.964 6,α2=2.629 7。 绘制的尽可能光顺的C1与C2连续过渡曲线如图5所示,过渡曲线的能量值曲线如图6所示。

图5 圆弧间尽可能光顺的C1与C2连续过渡曲线Fig.5 The C1and C2continuous transition curves between arcs as smooth as possible

图6 圆弧间过渡曲线的能量值曲线Fig.6 The energy curve of the transition curves between arcs
对于例2中给定的2条Bézier曲线,通过求解式 (11) 与 式 (12) 可 得 参 数 α1=3.384 0,α2=1.804 6。绘制的尽可能光顺的C1与C2连续过渡曲线如图7所示,过渡曲线的能量值曲线如图8所示。
3 过渡曲面的构造
对于图2所描述的问题,分别利用式(1)与式(2)表示的调配函数H1(t)与H2(t),可构造2类过渡曲面。

图7 Bézier曲线间尽可能光顺的C1与C2连续过渡曲线Fig.7 The C1and C2continuous transition curves between Bézier curves as smooth as possible

式中,-3≤ β1≤ 12。
定义4 给定2张参数方向相同的被过渡曲面Si(u,v)(i=1,2),称曲面

为第二类过渡曲面,其中H2(v)为参照式(2)表示的第二类调配函数,满足

图8 Bézier曲线间过渡曲线的能量值曲线Fig.8 The energy curve of the transition curves between Bézier curves
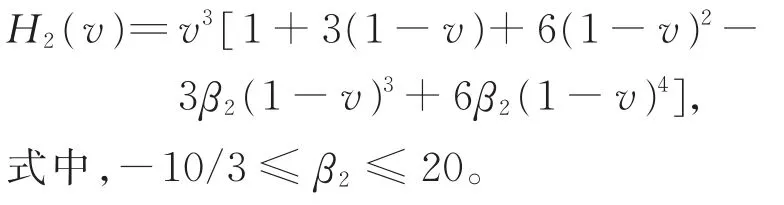
定理2 由式(13)与式(14)表示的2类过渡曲面具有以下特性:


(2)连续性:过渡曲面G1(u,)在过渡边界曲线S1(u,1)与S2(u,0)处满足C1连续,过渡曲面G2(u,)则在过渡边界曲线S1(u,1)与S2(u,0)处满足C2连续。
(3)形状可调性:当被过渡曲面Si(u,)(=1,2)保持固定时,过渡曲面Gi(u,v)(i=1,2)的形状可分别通过修改参数β1与β2的取值进行调节。
证明由式(3)与式(13)可得

式(15)表明,过渡曲面G1(u,v)与被过渡曲面在参数v方向保持一致,且在过渡边界曲线S1(u,1)与S2(u,0)处满足C1连续。
由式(4)与式(14)可得

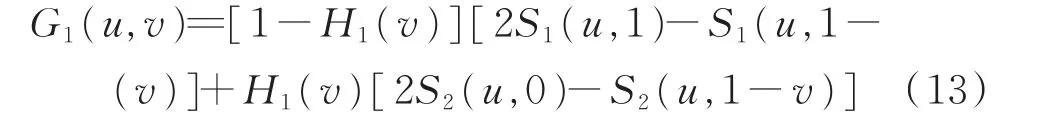
为第一类过渡曲面,其中H1(v)为参照式(1)表示的第一类调配函数,满足

式(16)表明,过渡曲面G2(u,)与被过渡曲面Si(u,)(i=1,2)在参数v方向保持一致,且在过渡边界曲线S1(u,1)与S2(u,0)处满足C2连续。
由于H1(v)与H2(v)中分别带有参数β1与β2,故由式(13)与式(14)可知,当被过渡曲面 Si(u,v)(i=1,2)保持固定时,过渡曲面Gi(u,v)(i=1,2)的形状可分别通过修改参数β1与β2的取值进行调节。证毕。
例4 设2张被过渡曲面Si(u,v)(i=1,2)的方程分别为
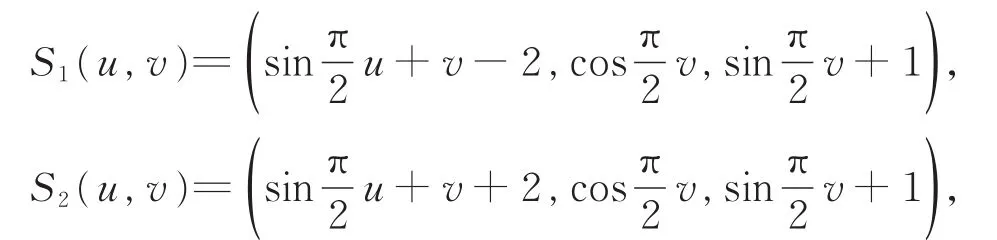
式中,0≤u,v≤1。 当参数β1与β2分别取不同值时,S1(u,v)与 S2(u,v)间形状不同的 C1与 C2连续过渡曲面分别如图9与图10所示。
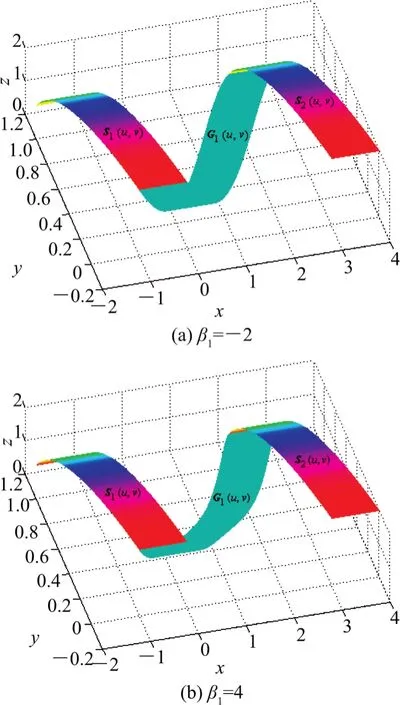
图9 参数取不同值时的C1连续过渡曲面Fig.9 The C1continuous transition surfaces with different parameters
注6 由图9与图10可知,当被过渡曲面Si(u v)(i=1,2)保持固定时,可分别利用参数β1与β2的取值实现对C1与C2连续过渡曲面形状的调整。注意到,参数β2对C2连续过渡曲面的形状较为敏感,故在实际应用中要根据具体情况选取合适的参数值。
与过渡曲线相似,也可通过调整参数β1与β2的取值使得构造的C1与C2连续过渡曲面尽可能光顺。下面给出参数β1与β2的确定方法。

图10 参数取不同值时的C2连续过渡曲面Fig.10 The C2continuous transition surfaces with different parameters
若记

则式(13)可改写为

据光顺准则[14],过渡曲面G1(u,v)的光顺程度可近似地由其能量值来刻画。能量值Es1越小,表明过渡曲面G1(u,)越光顺。

由于式(17)中带有参数β1(-3≤ β1≤ 12),因此,当被过渡曲面Si(u,)(i=1,2)保持固定时,要使过渡曲面G1(u,)尽可能光顺,只需确定使其能量值Es1尽可能小的参数β1的取值,即可得优化模型:

则使得C2连续过渡曲面G2(u,v)尽可能光顺的优化模型为

式中bi(i=1,2,3)为常数,分别为


式(19)与式(20)均为二次函数的条件最值问题,易求得参数β1与β2的值,再分别由式(13)与式(14)即可获得尽可能光顺的C1与C2连续过渡曲面。
注7当给定的被过渡曲面Si(u)(i=1,2)不可积时,式(19)与式(20)中对应的常数ai与bi(i=1,2,3)将无法通过计算获得精确值,此时可利用数值积分公式(如Simpson公式)计算其近似值。
例5 对于例4中给定的2张被过渡曲面,通过求 解 式(19)与 式(20)可 得 β1=-0.009 1,β2=3.013 3。绘制的尽可能光顺的C1与C2连续过渡曲面如图11所示,过渡曲面的能量值曲线如图12所示。

图11 尽可能光顺的C1与C2连续过渡曲面Fig.11 The C1and C2continuous transition surfaces as smooth as possible

图12 过渡曲面的能量值曲线Fig.12 The energy curve of the transition surfaces
4 结 语
为满足实际工程对过渡曲线曲面设计的高要求,基于2类带1个自由参数的调配函数,分别构造了满足C1与C2连续的过渡曲线曲面。所构造的过渡曲线曲面的优点有:(1)2被过渡曲线曲面可为任意的参数曲线曲面;(2)采用多项式形式,过渡曲线曲面的结构简洁,计算方便;(3)与2被过渡曲线曲面的参数方向保持一致,符合一般实际工程的需要;(4)含有自由参数,用户可轻松通过自由参数对过渡曲线曲面的形状进行调节。另外,还给出了通过能量优化模型确定自由参数的取值使得构造的过渡曲线曲面尽可能光顺的方法。如何在保参数方向构造既满足更高阶连续性要求,又满足形状可调的过渡曲线曲面,有待进一步研究。
