基于模糊控制的车道保持算法设计及仿真
2019-08-15谭蕊妮魏巍吕凤强
谭蕊妮,魏巍,吕凤强
(陕西重型汽车有限公司,陕西 西安 710200)
引言
目前,自动驾驶车辆是继新能源汽车后,我国汽车工业的又一个发展热点。国内主要整车企业均制定了相关的战略规划,一方面通过自主开发,掌握自动驾驶的基本技术;另一方面通过跨界合作,寻求产业融合及新的商业模式。主流观点认为,自动驾驶系统是分阶段实现的,任何企业直接进入终极阶段是不切实际的。因此,高级驾驶辅助系统(ADAS)作为初级阶段的典型代表,已经成为技术落地的研究热门,其中就包含车道保持技术。
1 车辆的横向控制
车辆控制是自动驾驶技术的研究核心之一,目的是能够根据感知及决策系统的结果,正确计算车辆所需的转向、油门和制动量,具体可分为车辆的横向与纵向控制。横向控制即转向控制,指如何计算合理的转角,使车辆能够沿规划的路径或保持在道路中心行驶,同时保证一定的安全与舒适性。纵向控制即油门和制动控制,通过计算合理的油门及制动量,使车辆按规划的速度或与前方动态目标保持一定的距离平稳安全的行驶。
车道保持是典型的横向控制应用,根据导航原理[1],可将其分为基于CCD 相机、GPS 系统和磁信号的车道保持方案。考虑信号质量和应用成本等因素,目前最常用CCD 相机识别车道线,所以根据这种传感器的特点,一般使用预瞄式横向控制方法。通过CCD 相机实时采集前方的车道线信息,计算与车辆相距一定预瞄距离处的偏差信息,如车辆距离车道中心的横向偏差,车辆轴线与道路中心切线的角度偏差等,基于车辆运动学或动力学模型计算相应的转角,达到消除偏差的目的,从而实现车辆的横向控制。
然而,汽车作为典型的时滞及高度非线性系统[2],其横向与纵向控制存在复杂的耦合关系。另外,车辆模型中涉及大量的经验参数,需要结合试验进行计算,难以保证准确性。所以如何进行解耦控制,使算法满足时滞和非线性需求,并且对一定范围内的车辆参数波动具有鲁棒性,是车辆控制领域的一个热点。针对这一问题,目前已有自适应控制、滑膜控制、模型预测控制和模糊控制等先进算法得到应用,并达到不错的效果。
2 基于模糊控制的车道保持算法
2.1 控制策略
在驾驶员操作车辆的过程中,并不需要对车辆参数做过多的了解,而是通过人为对外部环境的观察,调整车辆的航向及车速。所以,为了避免对车辆进行复杂的建模,考虑分析这种驾驶行为,并将其抽象为模糊规则。首先在驾驶过程中,驾驶员会观察车辆前方一定距离处的道路状况,并且该观察距离与车速有关,高速状态下距离较远,低速状态下距离较近。其次驾驶员将根据车辆与前方道路中心的横向偏差反向调整转向,即车辆位于道路中心左侧,则向右侧调整转向,反之亦然。最后驾驶员调整转向的幅度与当前车速有关,车速较低倾向于采用较大的幅度调整转向,反之则采用较为柔和的调整方式,以保证驾驶的安全。
因此,将横向偏差yL和当前车速Vx作为模糊控制器的输入,车辆前轮转角δ 作为输出,根据道路曲率规划车速,并采用一个合适的预瞄距离计算方式,即可实现一个完整的车道保持控制算法。
2.2 车道中心偏差和曲率计算
通常情况下,CCD 相机输出的感知结果为左右车道线参数。以左侧车道线为例,相机输出C0L~C3L四个参数,并基于一定的车道线模型计算偏差。本文采用螺旋车道线模型,设预瞄距离为z,那么与左侧车道线的横向偏差yLL及道路曲率CL可分别采用式(1)和(2)进行计算。
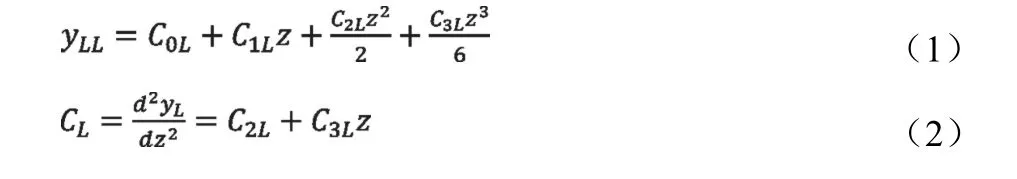
对于右侧车道线也具有同样的公式计算yLR和CR,分别根据yLL和yLR、CL和CR即能够估算出车道中心偏差yL和曲率C,用于模糊控制器和车速规划。
2.3 模糊控制器设计
根据文献[3],整个模糊控制器使用九个模糊集合,如表1 所示。模糊规则采用IF-AND-THEN 且为Mamdani 型推理,如表2 所示。隶属度使用三角形函数和梯形函数,如图1~3所示。
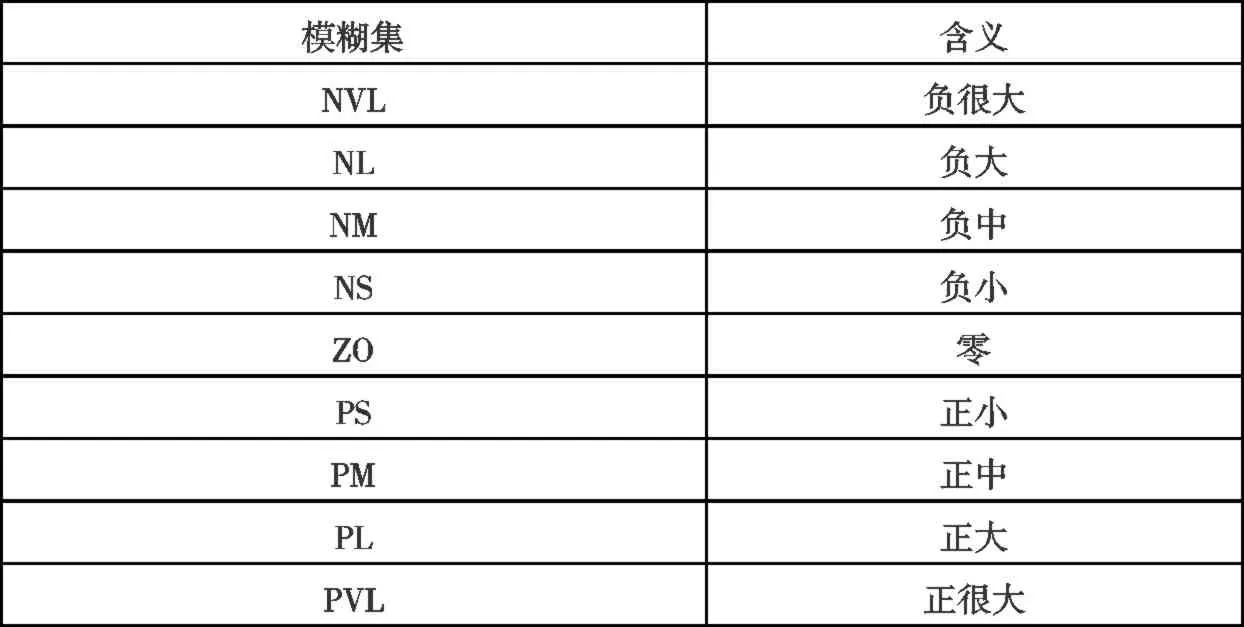
表1 模糊集合定义
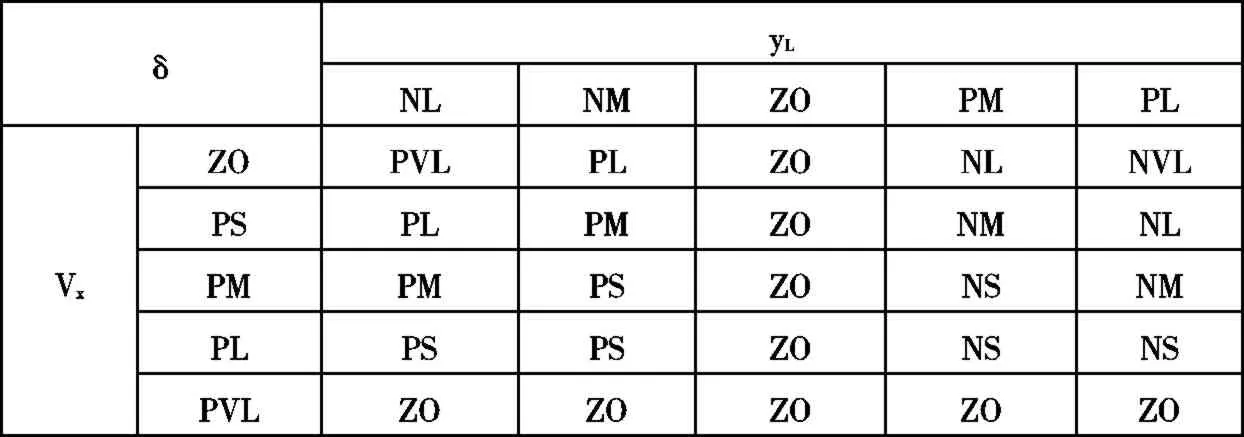
表2 模糊规则
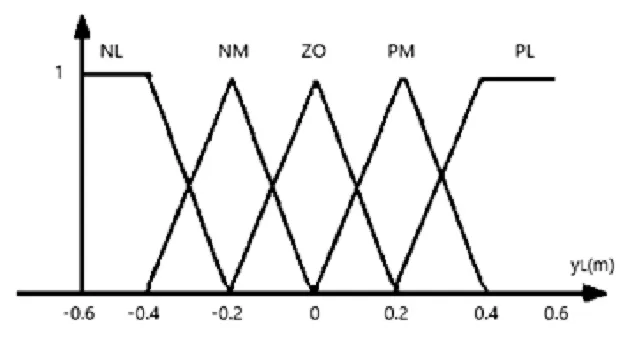
图1 横向偏差yL 的模糊集合划分
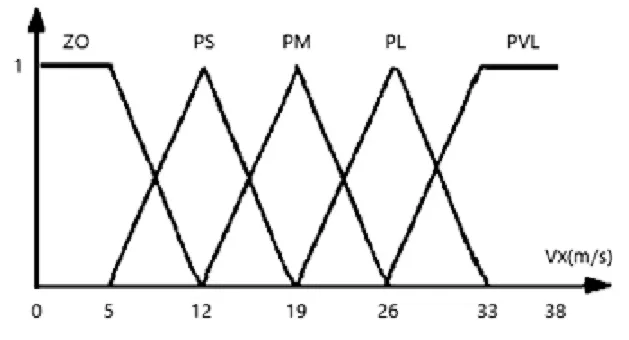
图2 当前车速Vx 的模糊集合划分
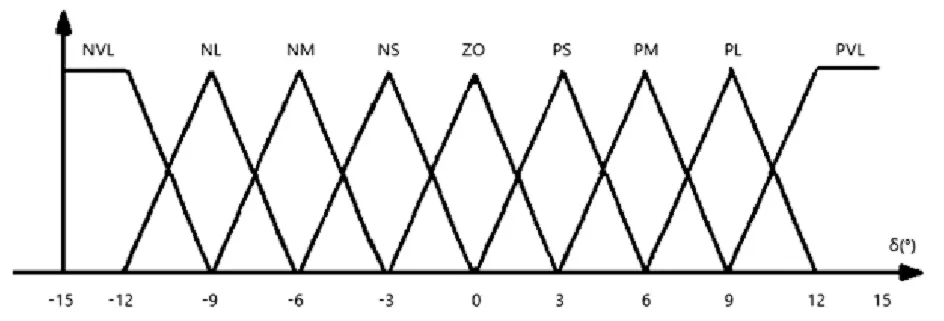
图3 前轮转角δ的模糊集合划分
2.4 车速规划
为保证驾驶安全,将车道保持的最高车速设置为70km/h,并根据预瞄的车道曲率C 确定目标车速,如表3 所示。
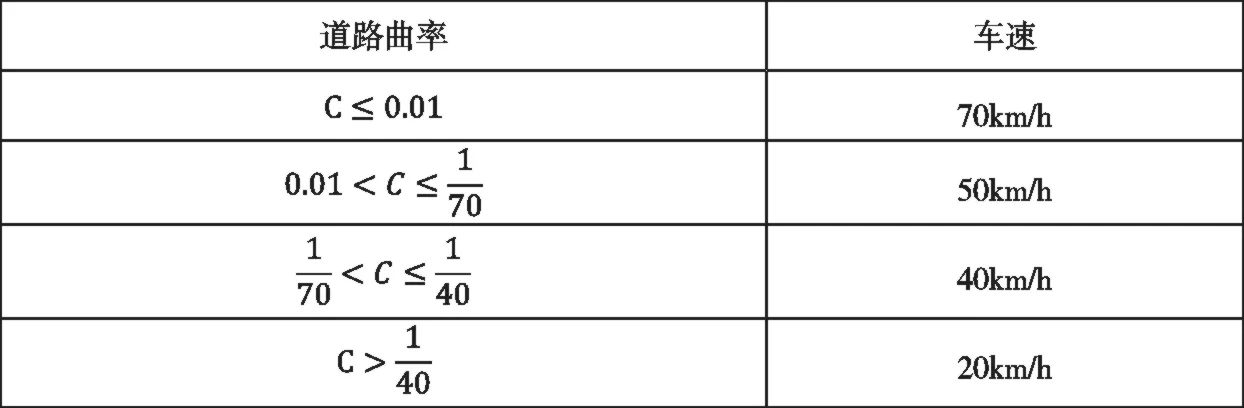
表3 道路曲率和车速的关系
最后根据目标车速VP和当前车速Vx,利用式(3)求得需要的加速度Acc(其中T 为采样周期)。注意,由于车辆执行机构的限制,需要对Acc进行限幅。

3 基于Matlab/Simulink 的算法模型
Matlab 2018a 中提供了自动驾驶工具箱(Automated Driving System Toolbox)和车辆动力学工具箱(Vehicle Dyna-mics Blockset),可以方便的创建简单的驾驶场景,模拟CCD相机感知的结果,以及创建车辆动力学模型,并具备相当的仿真精度。所以选择Matlab2018a 为平台,搭建算法模型并进行仿真,如图4 所示。
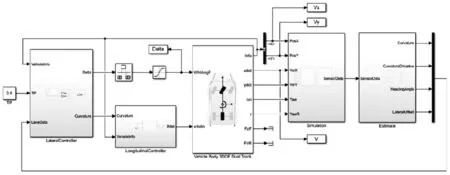
图4 基于模糊控制的车道保持算法模型
其中,子模块Simulation 用于读取创建的驾驶场景,Estimate 用于估计车道中心参数,LateralController 为模糊控制器,LongitudinalController 用于车速规划。整个模型的采样周期为0.01s,为防止转向频繁抖动,使用Rate Transition模块降低转角的输出频率为0.1s。以当前车速Vx与预瞄时间TP相乘的方式计算预瞄距离,并限制最小和最大预瞄距离为5.6 和15m。车辆使用二自由度单轨动力学模型表示,具体参数如表4 所示。
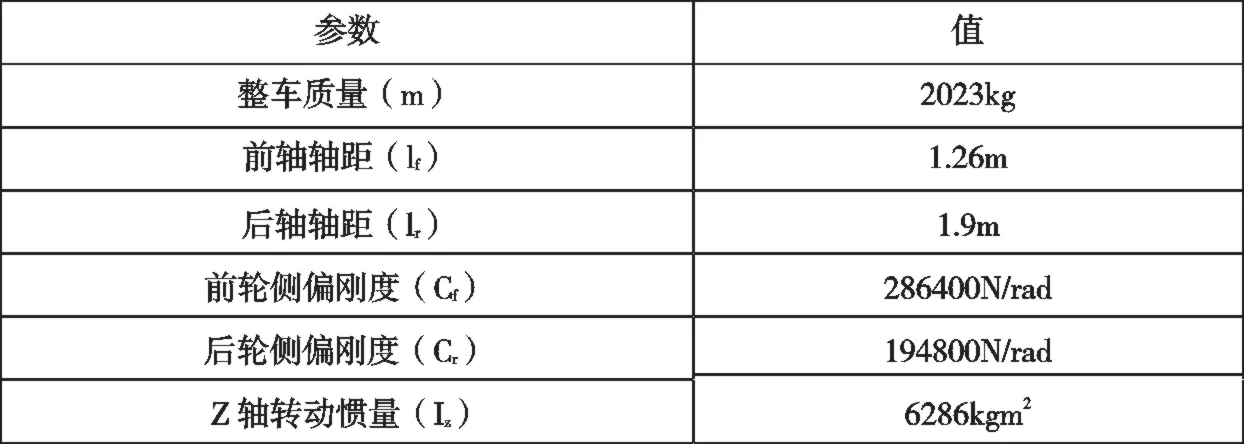
表4 仿真车辆的动力学参数
4 仿真结果
算法仿真结果如图5 所示,可见该算法能够控制车辆通过车道中心点,并且转角变化较为平稳,在转弯较急处,车辆有明显的减速过程。整个算法的设计简单,执行效果较好,具备一定的应用价值。
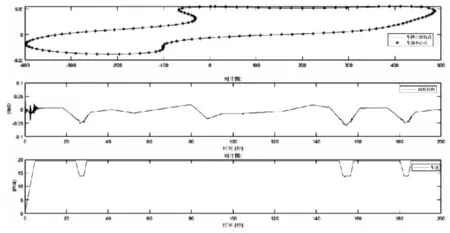
图5 车道保持算法仿真结果
