基于遗传算法的移动Sink数据采集信宿路算法*
2019-08-14谢英辉唐一韬
谢英辉,胡 君,唐一韬
(1.长沙民政职业技术学院软件学院,长沙 410004;2.湖南科技职业学院软件学院,长沙 410004)
随着对信息收集需求的加强,无线传感网络WSNs(Wireless Sensor Networks)[1]被广泛应用于多个领域[2],如康复医疗、智慧农业。WSNs是通过在监测区域内部署微型传感节点,并由微型传感节点感测数据,再将数据传输至后台。然而,这些传感节点属微型节点,一般是由电池供电。它们的节点能量有限,且传输感测数据需要多跳转发,这限制了WSNs的应用[3]。
传统的WSNs中,传感节点通过多跳方式向固定的基站传输数据,这容易使得基站附近的节点参与过多的数据转发,消耗了它们大量的能量。为了延缓节点能量消耗,并提高数据收集效率,研究者提出基于移动Sink的数据收集方案。
依据Sink的移动路径,基于移动Sink的数据收集方案可分为固定移动、随机移动和受控移动。例如,文献[4]提出移动路径选择算法(Moving Path Selection Algorithm,MPSA)。MPSA算法依据虚拟力决策移动方向。而文献[5]引用启发式算法,并依据节点的任务负荷设置优先级,进而减少网络拥塞和时延。同时,该算法利用SMT设置虚拟访问点,规划Sink节点访问路径。此外,Bhadauria等[6]依据网络内节点密度对Sink的移动进行调整,并提出基于节点密度不同的Sink移动速度控制方案。
尽管移动Sink方案能够有效地提高数据收集率,但是该方案仍存在一个问题必须解决:Sink的移动路径的规划。显然,移动路径的不同,节点所收集的数据可能不同,网络能量消耗也会不同。因此,如何规划Sink的移动,进而最大化数据收集效率是基于移动Sink数据收集方案的关键技术。
目前,有两个策略规划Sink的移动路径:①移动Sink遍历网络内所有传感节点;②移动Sink只遍历一些预先设定的位置,这些位置称为驻留点RZP(Rendezvous Point)[7]。相比第一个策略,引用RZP的路径规划策略效率更高,能耗更少。图1显示了依据RZP收集数据的示意图。移动Sink通过遍历RZP,形成数据收集路径。

图1 基于移动Sink的数据收集过程
然而,求解RZP是一个NP问题,其受到多个因素影响,如节点能量、节点密度。而遗传算法GA(Genetic Algorithms)根据适者生存,优胜劣汰等自然进化规则来进行搜索计算和问题求解。对许多用传统数学难以解决或明显失效的复杂问题,特别是优化问题,GA提供了一个行之有效的新途径。
简之,GA模拟自然界优胜劣汰的进化现象,把搜索空间映射为遗传空间,把可能的解编码成一个向量——染色体,向量的每个元素称为基因。通过不断计算各染色体的适应值,选择最好的染色体,获得最优解。
为此,提出基于遗传算法的移动Sink数据采集算法GMSDC(Genetic algorithm-based Mobile Sink Data Collecting)。GMSDC算法利用遗传算法寻找最优的驻留点,Sink再依这些驻留点移动,进而构成最优的数据传输路径。仿真数据表明,提出的GMSDC算法有效地缩短了数据收集时间,并降低了Sink移动路径。
1 系统模型及问题描述
1.1 系统模型
假定n个传感节点随机分布于M×M的方形区域,并形成自组织的网络拓扑。此外,传感节点和Sink节点受以下约束条件限制:①传感节点是静止的。一旦部署后,传感节点不再为移动,且每个传感节点具有唯一的标识;②所有传感节点具有相同的通信半径r;③Sink节点能够移动,且它不受能量约束。
1.2 问题的形式化表述
对给定的节点集S={s1,s2,…,sn}、RZP点集Ω={z1,z2,…,zm}构建无向图G=(V,E),其中V=S∪Sink,E为边集合[8]。令R0表示基站位置。令hi,j表示第ith传感节点与第jth个RZP点间的距离,且1≤i≤n,1≤j≤m。类似地,令di,j表示第ith个RZP点与第jth个RZP点间的距离,且1≤i≤m,1≤j≤m。
令τ表示Sink在收集数据时所移动的路径长度,其定义如式(1)所示:
τ=∑di,j+d1,R0+dm,R0
(1)
式中:d1,R0、dm,R0分别表示第一个RZP点、最后一个RZP点离基站的位置。
提出的GMSDC算法旨在通过GA搜索最优的RZP点,并由这些RZP点构成Sink移动路径,使Sink覆盖全网络,以最短的移动路径实现采集数据的最大化。令m*表示最优的RZP点数,且m*≤m。
因此,可建立式(2)的目标函数:
Minimize(τ)
(2)
约束条件:

2 GAFR算法
GA在求解工程数学问题方面得到广泛应用。GA主要涉及到个体(Individual)、适度生存、适应性(Fintess)、群体(Population)、复制(Reproduction)、交配(Crossover)和变异(Mutation)用语。表1这些用语在工程数学领域的解释。

表1 GA算法中关键用语的解释
图2描述了GA执行流程。选设定初始群体,并确定种群,再计算各染色体的适应度。随后,通过存优去劣法则产生新的种群[9],并检测是否满足预定指标。若满足,则获取解,否则继续迭代。

图2 GA的执行流程
2.1 染色体编码
GMSDC算法旨在构建最优的RZP,即寻找最优的m*。为此,将RZP的IDs编码成染色体,而染色体的长度等RZP的数目。当Sink移动至RZP就收集附近传感节点的数据。
RZP的ID就是染色体的基因位置。图3显示了两条染色体。第一条染色体具有10个基因位置,第二条具有12个基因位置。可通过交叉操作改变染色体长度。

图3 染色体编码
2.2 种群
对于不同长度的染色体,均采用固定的初始群体尺寸。若采用初始群体数为N,则只要满足群体数为N的染色体才是有效的[10]。群体数反应了可行解数。图2显示了长度为10、12的两条染色体,但它们的群体数均为5(N=5)。
2.3 适度函数
GA利用适度函数评估染色体的性能,分析它们适应环境的能力,使更优质的基因得到进化。Sink移动路径与RZP数密切相关,也与路径长度相关。
为此,构建如式(4)所示的适度函数:
F=αL+βτ
(4)
式中:L表示迭代过程中驻留点数,且L≤m。而α、β为权重因子,用于平衡L和τ对适度值F的影响,且α+β=1。
L和τ均为系统因子,是在推导驻留点数m*过程中的系统变量。如图4所示,最初先部署RZP,通过GA算法迭代L值,然后判断是否满足条件。若满足,就输出最优m*值,否则就继续迭代。本文通过迭代次数设置终止条件。

图4 优化RZP的过程
2.4 选择阶段
选择部分染色体进行交叉、变异,进而产生新的种子是GA算法的关键。而所选种子的优劣直接与染色体的适度值相关。换而言之,可通过染色体的适度值选择种子。
目前,有多类选择算法,如轮盘赌选择、秩值选择法。本文选用轮盘赌选择法,其基本思想是:个体被选中的概率与其适应度大小成正比。轮盘赌选择的执行步骤如下所示:
Step 1:计算群体中每个个体的适应度f(xi)i=1,2,…,M
Step 4:从[0,1]区间内产生一个均匀颁的随机数b
Step 5:若b Step 6:重复执行步骤(4)、步骤(5),共M次 利用2.4选择部分染色体,再对这些染色体进行交叉操作。现存在单点、多点交叉。本文选择单点交叉[11],如图5所示。最初,两条染色体的长度分别为8、12。通过交叉操作,产生长度为10的新的两条染色体。 图5 染色体交叉示意图 GA使用交叉操作已经从全局的角度出发找到了一些较好的个体编码结构,可能已经接近问题最优解,但是用交叉操作无法对搜索空间的细节进行局部搜索,因此通过变异操作[11-12]调整个体编码串的部分基因值,提高遗传算法的局部搜索能力。 令变异概率为0.5。每条染色体进行均进行变异,进而提高染色体质量。如图6所示,染色体2的第5个基因位置发生变异,由原来的77变成64。 图6 变异后的操作 通过Python3.5软件构建仿真平台,分析GMSDC算法的性能。考虑在M×M的方形区域部署50~300个传感节点。Sink的移动速度为ϑ=5 m/s,并在驻留点处停留1 s。具体的仿真参数如表2所示。此外,选择能量高效的移动Sink数据收集策略(EDAMS)[8]作为参照,并分析Sink所移动的路径以及收集数据所需要的时间。 表2 仿真参数 为了更好地节点密度对算法性能的影响,考虑两场景。场景一:M=10 m;场景二:M=15 m。 3.2.1 场景一 图7显示了Sink移动的路径长度随节点数的变化情况。从图7可知,路径长度随节点数的增加而上升。这主要因为:节点数越多,Sink需要收集的数据越多,就增加Sink的移动路径。此外,相比于EDAMS算法,GMSDC算法缩短了Sink移动路径。这主要因为:GMSDC算法通过遗传算法寻找最优的RZP,以最短的路径完成了数据的收集。 图7 路径长度(场景一) 图8显示了Sink收集数据所耗的时间。时间越短,数据收集效率越高。从图8可知,节点数的增加拉长了Sink收集数据时间。原因在于:节点数越多,节点移动路径越长,必然增加了节点收集数据的时间。相比于EDAMS,GMSDC算法的数据收集效率更高。例如,在节点数为250时,EDAMS算法的数据收集时间达到6 000 s,而GMSDC算法的数据收集时间只有2 200 s。 图8 数据收集时间(场景一) 图9 路径长度(场景二) 3.2.2 场景二 本次实验考虑更大仿真区域,仿真区域面积为200 m2。图9、图10分别显示了在仿真区域200 m2下的Sink移动路径和数据收集时间。 从图9可知,Sink移动路径仍随节点数的增加而上升。相比图7,仿真区域面积的增加,加大了路径长度。原因在于:区域面积越大,节点移动路径必然增加。例如,在节点数为300时,当区域面积从100 m2增至200 m2时,EDAMS和GMSDC算法的路径长度分别从1 350、450增加至2 500、900。 图10显示了数据收集时间随节点数的变化情况。从10可知,节点数的增加提升了数据收集时间。相比于图8,仿真区域200 m2下的两个算法的数据收集时间更长。例如,在节点数为250时,当仿真区域为200 m2降至100 m2时,GMSDC算法的数据收集时间从5 800 s降至约13 000 s。 图10 数据收集时间(场景二) 3.2.3 Sink的移动特性分析 本次实验分析移动速度以及在RZP的停留时间对移动路径长度以及数据收集时间的影响。实验参数:仿真区域为100 m2,节点数300。 从图11可知,Sink移动速度的增加,降低了路径长度,这符合预期。移动速度的加快,加速了GA算法收敛的速度。此外,观察图11不难发现,在RZP停留时间对路径长度影响并不大。在0.5 s~3 s的停留时间内,路径长度波动范围小。 图11 GMSDC算法的路径长度随Sink移动 特性变化情况 快速有效地收集数据是多数基于WSNs应用的关键。而移动Sink是快速收集数据的有效措施。考虑到Sink的移动路径受多方因素影响,GMSDC算法引用GA算法选择RZP点,Sink就依着这些RZP点所构成的路径进行移动。仿真结果表明,提出的GMSDC算法减少了数据收集时间。2.5 交叉

2.6 变异

3 性能分析
3.1 仿真环境

3.2 数据分析



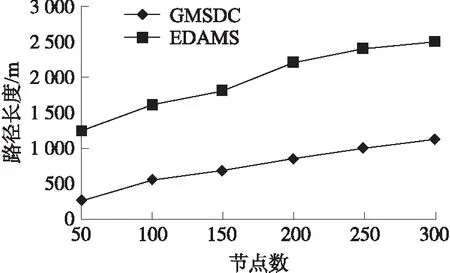

4 总结
