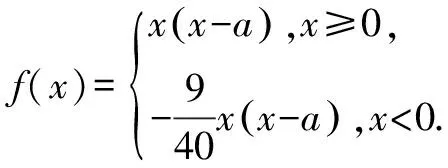左顾右盼话分段函数
2019-08-14冯寅
冯 寅
(浙江省湖州中学 313000)
分段函数是高中阶段常见的函数形式,由于它在不同的区间上的表达式不同,所以在解决问题时一定要关注在不同段上的表达式的特点,这样才能从整体上处理好分段函数的问题.
一、左右交替的求值
求分段函数的某个函数值,是和分段函数有关问题中最常见的,所求的函数值往往和分段函数的不同形式都有关系,这时要求我们注意每段的条件,经常在不同分段中交替求值.
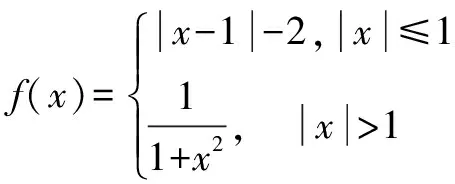
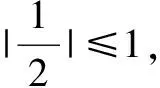
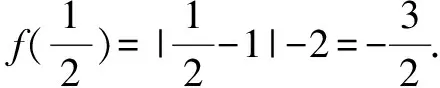


分析这个问题想要求出f(f(a))的表达式比较困难,它即和a的范围有关,也和f(a)的范围有关,这样的分类讨论很困难,所以我把f(a)看成一个整体来分类讨论.
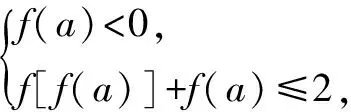
二、左右衔接的单调
在分段函数中研究函数的单调性,要分别考虑不同段的单调性,还要考虑在分段点处的衔接,分段点的不同取值可以保持或改变两段的单调性.
问题3 已知a>0,函数f(x)=

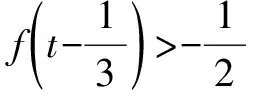
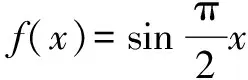
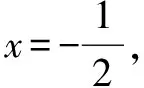
下面观察分段点x=0的情况.
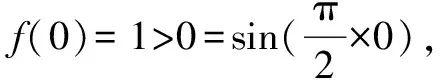



然后考虑在分段点的函数值情况,应该满足函数y=(3a-1)x+4a在x=1时的函数值,不小于函数y=logax在x=1时的函数值,即(3a-1)+4a≥0. (2)
三、左右交叉的奇偶
函数的奇偶性必须研究定义域范围内的所有实数,所以研究分段函数奇偶性时要注意每段都要研究,并且注意每段都要兼顾交叉.
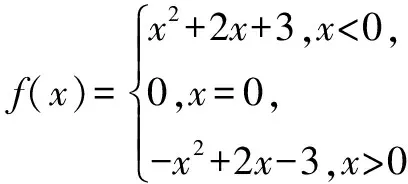
分析判断函数的奇偶性必需按照奇偶性的定义,对定义域内的所有实数进行分析验证,对分段函数的情况,函数的取值还要考虑分段函数的要求.
当x>0时,-x<0,则f(-x)=(-x)2+2(-x)+3=x2-2x+3=-f(x);
当x<0时,-x>0,则f(-x)=-(-x)2+2(-x)-3=-x2-2x-3=-f(x);
当x=0时,f(-0)=-f(0)=0.
因此,函数f(x)是R上的奇函数.

分析此题的关键是如何利用f(x)为R上的奇函数的条件,确定g(x)的表达式.

因此g(x)=-x2+2x,所以g(-1)=-3,f(g(-1))=f(-3)=g(-3)=-(-3)2+2×(-3)=-15.
四、左右分割的零点
分段函数的零点由于在不同段的函数表达式不同,所以要分段独立思考,通过不同段上的研究再整合为整体的情况.
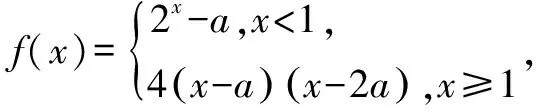
分析1 代数方法分类讨论.
从分段函数的解析式可知,f(x)=2x-a在区间(-∞,1]上是增函数,所以最多只有一个零点. 设零点为x0,即f(x0)=0,则2x0-a=0,则x0=log2a,因此,0 下面对a进行讨论,研究函数整体的零点存在情况. (1)当a≤0时,f(x)=2x-a(x<1)无零点;f(x)=4(x-a)(x-2a)(x≥1)无零点! (2)当0 (3)当a≥2时,f(x)=2x-a(x<1)无零点;要使原函数有且只有两个零点,必须f(x)=4(x-a)(x-2a)(x≥1)恰有两个零点a,2a,故a≥2. 分析2 利用函数图象分析 (1)当a≥1时,因为f(x)=4(x-a)(x-2a)(x≥1)已有两个零点a,2a,要使f(x)恰有两个零点,必须f(x)=2x-a(x<1)无零点. 作出函数的图象(图1),可知2-a≤0,即a≥2. (2)当a<1时,因为f(x)=2x-a(x<1)有一个零点,要使f(x)恰有两个零点,必须f(x)=4(x-a)(x-2a)(x≥1)只有一个零点. 当分段函数遇到函数的最大(小)值问题时,一般都会先分段确定函数的最大(小)值,再根据条件对确定的最大(小)值进行分析比对,找到符合整体要求的最大(小)值. 从上述的五个方面的研究,我们可以看出分段函数的性质研究,必需在函数性质研究的基础上关注不同段上函数性质的特点,通过每段的分解、合成、交叉解决分段函数的问题.
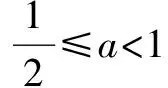
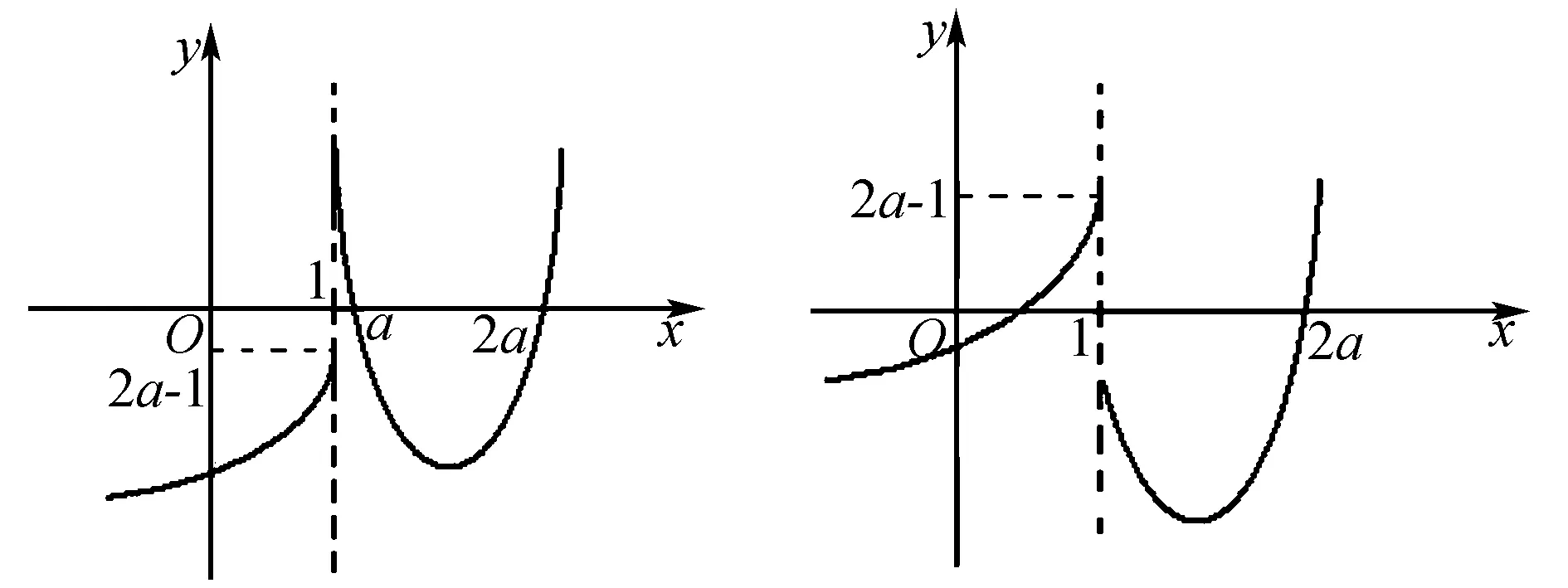

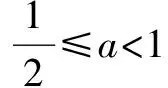
五、左右比较的最值