高三复习中“一类函数的最值”问题的探索与思考

张先宏

(安徽省含山中学 238100)

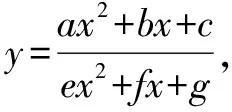
一、分式函数的探索

本文介绍的分式函数在高考中常考，其分子和分母均由函数式构成，且函数结构随着a、b、c、e、f、g取值的变化而变化.当a、e为零时，函数变成“一元一次分式函数”，求解难度降低；当a、e不全为零时，函数结构为“一元二次分式函数”，求解难度增加.不仅如此，常数的改变会引起函数结构的改变，都会影响求解难度，同时，由于分母不能为零，函数的定义域对最值也会有影响.求解此类函数时应密切注意分子与分母的关系，以求最简易的解题方法.

二、分式函数多种题型的解析

1.当a、e为零时

2.当a、e不全为零时

此时，函数变为“一元二次分式函数”，这类函数最值求解难度大，且情况多，更复杂，下面进行分类讨论：

(1)当函数可以进行分母分子约分时

(2)当函数分子分母不能进行约分时

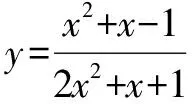
这道函数题不能约分简化，怎么办呢？易知分母不可能为零，x的取值范围为R，可以对函数化整变形得到：(2y-1)x2+(y-1)x+y+1=0.

显然，2y-1≠0时函数式变成了关于x的一元二次方程，因为原函数中x的取值范围为R，所以方程一定有实根，这时，我们应该想到方程有实根的判定方法，即判别式大于等于0，此题中即：(y-1)2-4(2y-1)(y+1)≥0，解不等式，就能得到函数最值，这里不进行求解.

(3)当x的取值范围受到区间限制时

3.均值不等式法求解

本文对人教版数学高三复习一类分式函数的最值求解进行了分析探讨，介绍了分式函数的各种形式以及不同的解答方法，其解答方法多种多样，加上其各系数的改变也会影响解答方法的选择.所以，学生需要努力掌握每种方法，不仅要会做题，更要理解其本质，掌握各区块的知识点，在高考时碰到类似题型才能迎刃而解，从而在高考数学中取得自己满意的成绩，为自己未来的人生打下良好的基础.