基于试题的知识拓展研究——抽象函数的几个性质和函数的图象特征

杨苍洲

(福建省泉州第五中学 362000)

一、试题研究

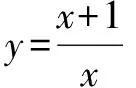
A.0 B.mC.2mD.4m

分析本题主要考查函数的对称性、函数的零点等基础知识，考查运算求解能力、应用意识，考查数形结合、转化与化归等数学思想等.解答本题的关键在于掌握下述两个教材边上的重要知识：

知识点1若函数f(x) (x∈R)满足f(-x)=2-f(x)，则函数f(x)的图象关于点(0,1)成中心对称.

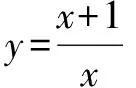
二、拓展与延伸

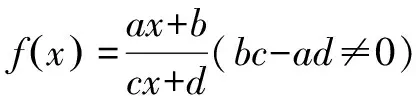
1.抽象函数的几个性质

性质1 函数f(x)(x∈R)满足f(x+a)=f(x+b)，则T=|b-a|是函数f(x)的一个周期.

性质2 函数f(x)(x∈R)满足f(x+a)=-f(x+b)，则T=2|b-a|是函数f(x)的一个周期.

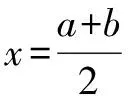
上述四个性质，表述相近，形式相似，因此我们把他们放在一起进行辨析.实际上，性质2的条件可更改如下：

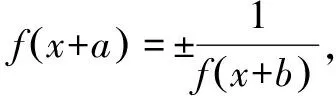
性质4可更加一般化为：

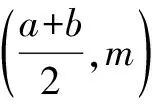
上述问题的解答就是应用了性质6.

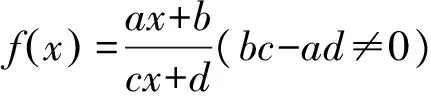
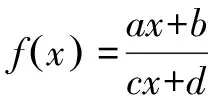
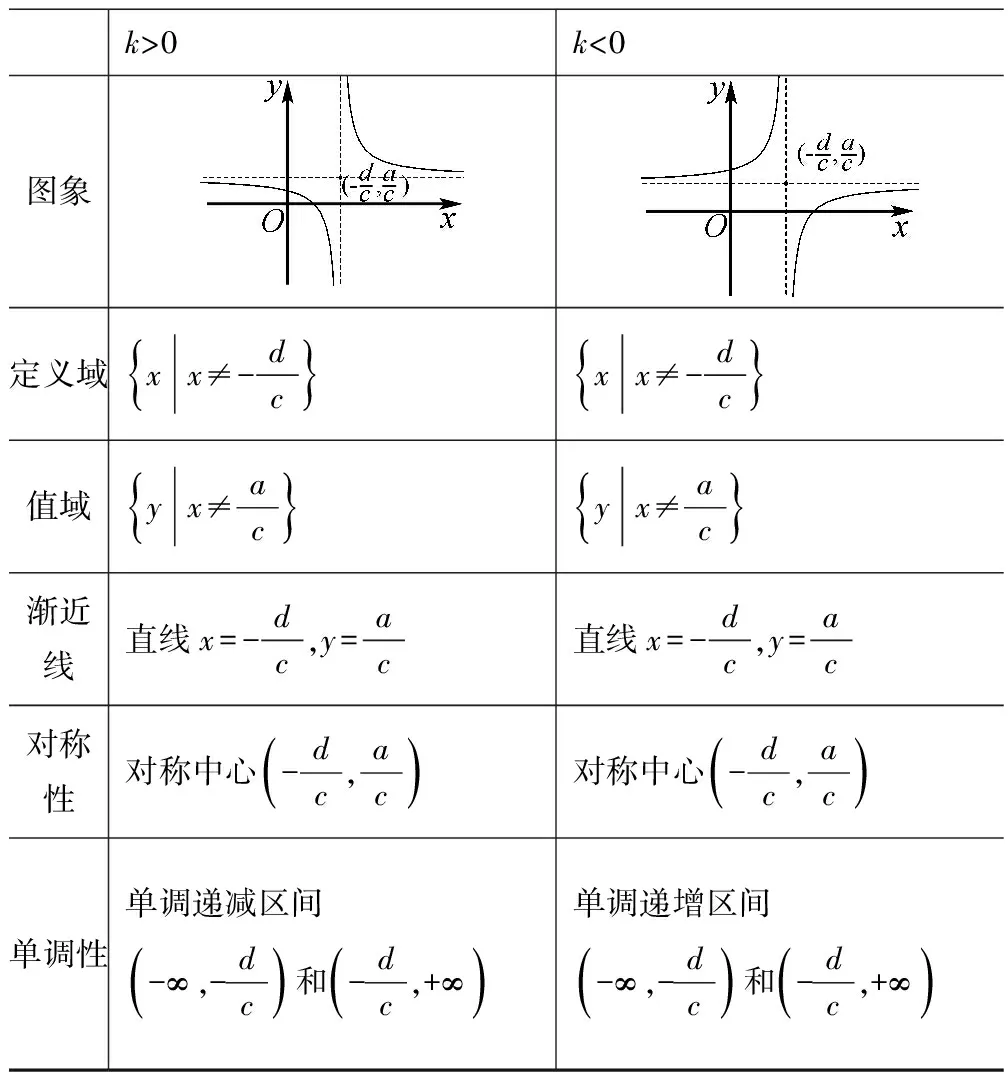
k>0k<0图象定义域xx≠-dc{}xx≠-dc{}值域yx≠ac{}yx≠ac{}渐近线直线x=-dc,y=ac直线x=-dc,y=ac对称性对称中心-dc,ac()对称中心-dc,ac()单调性单调递减区间-∞,-dc()和-dc,+∞()单调递增区间-∞,-dc()和-dc,+∞()

如何快速作出函数f(x)的图象呢？