Spark框架下基于对比散度的网络服务TLRBM推荐算法
2019-08-14那勇
那 勇
(吉林省远程教育技术科技创新中心 吉林 长春 130022) (吉林广播电视大学远程教育技术中心 吉林 长春 130022)
0 引 言
Web服务是可通过网络互通信的计算机应用程序,由服务提供商根据用户需求开发,随着互联网用户需求的不断增加,Web服务利润增长潜力巨大。许多服务提供商倾向于结合业务和营销计划进行Web服务开发,这会导致多个提供商可提供功能相似的服务。同时,Web服务推荐过程中,服务质量取决于多种因素,如网络传输带宽、实现机制和硬件等[1-2]。因此,用户希望从服务提供商获得理想QoS的Web服务,例如延迟、可用性和可靠性等。然而,目前几乎所有的服务提供商都关注利润,每个服务的QoS属性都由服务提供商预先确定,但在其推广过程中,服务提供商常常对Web服务QoS进行夸大以吸引更多的用户。因此,QoS合理评价是面向应用的Web服务推荐的重要应用之一。
协同过滤推荐是Web服务推荐的主要方法,主要分为两类[3]:模型协同过滤和内存协同过滤,其中内存协同过滤采用的是Web服务评分矩阵方式进行项目的推荐和预测,常用到聚类分析算法,但是在每次计算中都需要对这个评分矩阵进行计算,算法的通用性不强;而模型协同过滤算法则是根据Web服务评分矩阵进行评价模型的演化,在后续的Web服务推荐过程中采用的就是模型预测方式取代原有评分矩阵方式,有助于提高算法计算普适性和精度。评分矩阵的模型构建方式很多,例如贝叶斯方法、马尔可夫方法、受限玻尔兹曼机RBM(Restricted Boltzmann Machine)方法等[4]。相对而言,近年来RBM方法得到了学者们更多的研究,其采用无向图方式进行模型构建,因此可得到鲁棒性更强的评价模型,其采用可见层和隐藏层两层模型形式。已有很多文献研究了RBM方法应用于推荐系统的实现方式,例如文献[5]提出一种基于RBM方法的推荐问题求解策略,利用隐藏层权重共享实现算法性能的提升。文献[6]同样基于RBM方法设计了一种推荐问题求解策略,其将实值推荐问题表示为多维0-1向量表示问题,对RBM方法进行了模型扩维,虽然提高了推荐算法的精度,但降低了算法的执行效率。通过分析已有文献,虽然都针对某些方面进行了改进和实现提高了算法的性能,但是在互联网大数据时代,传统的Web推荐方法在实现过程中存在两个方面的问题:(1) 算法的自学习更新问题。现有算法模型多是固定式模型,其对于特定的Web服务推荐形式有效,但是通用效果不佳,实际应用效果不理想。Web服务推荐某些应该根据时间和需求等因素的变化具备自学习的能力,这样才能提高算法的适应性和应用价值。(2) 具有学习能力的算法,比如神经网络算法等,虽然具备一定的学习性能,但是算法的计算过程非常复杂,算法的时效性无法得到有效满足。对大数据的处理,如何采用并行计算方式进行模型效率提升问题,提高算法的执行效率,是提升算法应用价值的另一个重要因素。这两个问题是制约RBM方法在Web服务推荐过程中的应用成功与否的关键。
为了克服上述缺点,本文提出一种基于Spark框架下的基于两层受限玻尔兹曼机的Web服务质量预测模型,并基于用户之间的直接信任关系,提出了一种基于受限玻尔兹曼机的Web服务质量预测模型。同时为提高算法处理Web服务大数据的并行化执行能力,采用了对比散度算法来提高收敛速度,并考虑了大数据情形采用Spark框架实现TLRBM模型的快速执行算法,大幅度提升了Web服务推荐算法的计算速度。
1 理论介绍
1.1 受限玻尔兹曼机
受限玻尔兹曼机模型结构的无向二部图如图1所示,具有m个可见单元V=(v1,v2,…,vm),以及n个隐藏单元H=(h1,h2,…,hn)。其中:V表示可观测数据,H是观测变量之间的相关性。与传统玻尔兹曼机相比,RBM模型结构中同层节点之间没有关联性,其可见层和隐藏层的联合构型(V,H)具有能量函数:
式中:vi和hj分别是可见单位i和隐单元j的二进制状态;bi表示第i个可见节点的偏差,cj表示第j个可见节点的偏差;wij是单元vi和hj之间的边缘相关联的实值权重。
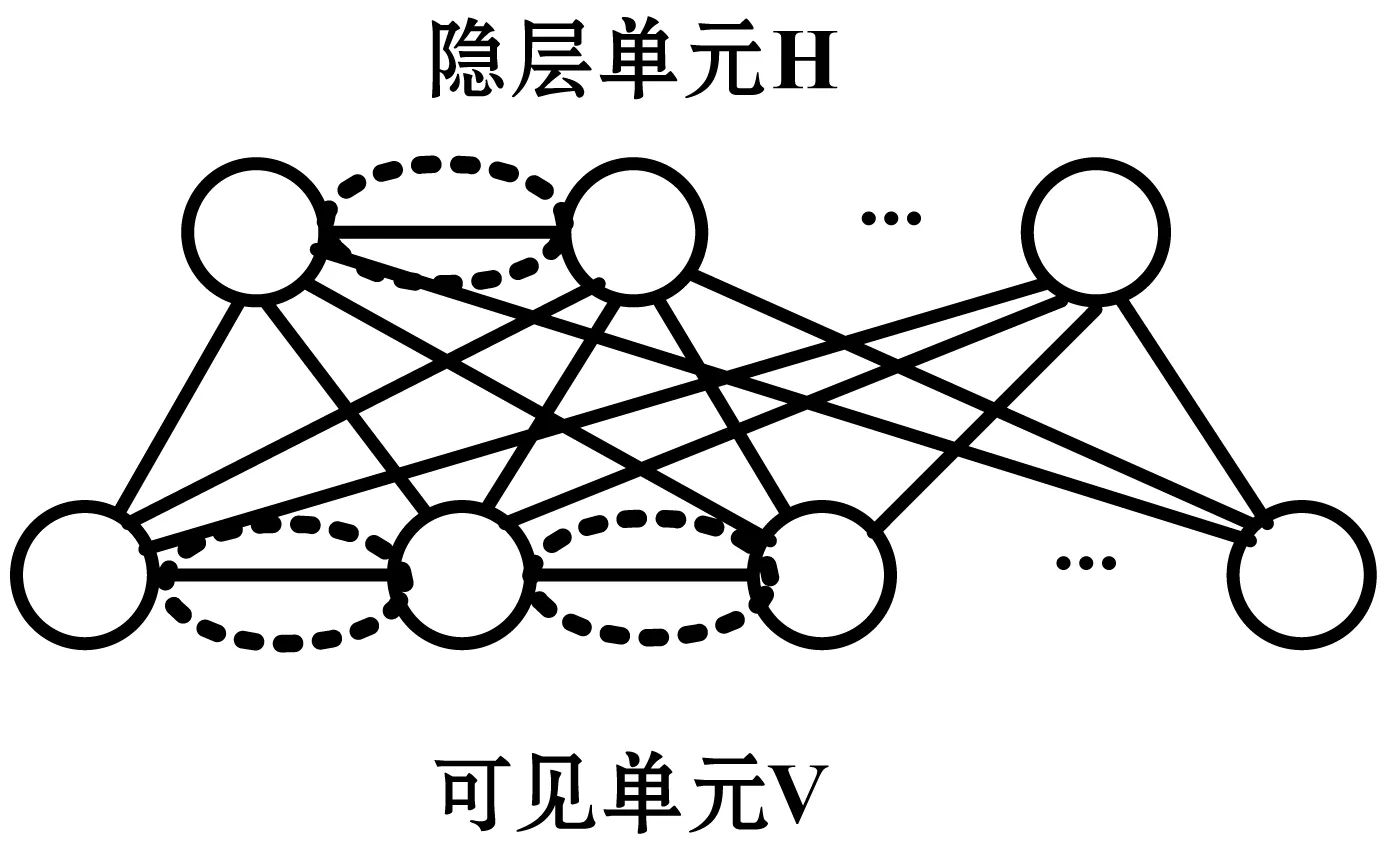
(a) 玻尔兹曼机
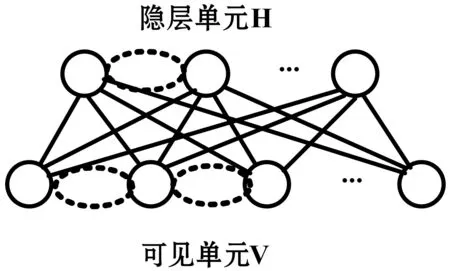
(b) 受限制玻尔兹曼机图1 受限制玻尔兹曼机与传统玻尔兹曼机对比
该模型下的联合概率分布是通过Gibbs分布p(v,h)=1/Ze-E(v,h)求出所有可能的可见和隐藏向量对,其中Z=∑v,he-E(v,h)。因为隐藏单元之间没有直接联系,所以可简单的获得无偏样本数据〈vihj〉data的条件概率如下:
类似地,可见单元之间没有直接联系,可获得无偏样本〈vihj〉model的条件概率如下:
式中:sig(x)=1/(1+e-x)是Logistic函数。为了处理数据,可通过调整权重和偏差来提高节点的概率,以降低该节点的能量并提高其他节点的能量,特别是在低能量情况下。因此,它对分割函数有很大的贡献。具有权重的训练向量的对数概率的导数为:
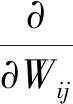
(4)
式中:〈…〉是Gibbs分布的期望。
式(3)可以反复计算直到样本向量均位于可见层上,隐藏层是条件独立的,并且来自〈…〉的无偏样本,使用对比散度(CD)学习会使结果快速收敛。
1.2 用户信任度计算
Web服务推荐过程中需要使用到用户的评价问题,一般采用信任网络模型进行表示,该网络模型采用有向图G=(U,E)表示,其中模型参数U表示信任网络模型节点集,Web服务在网络中以节点形式进行表示;E表示信任网络模型的边集,信任值在网络中以节点之间的边值wi形式进行表达,具体如图2所示(以6个Web服务信任网络模型为例)。
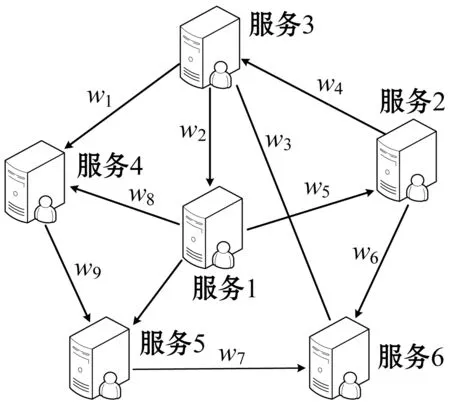
图2 信任网络模型(6个Web服务)
图2所示信任网络模型中节点之间的信任值一般采用[0,1]区间内的实数进行表示,其可表征节点之间的信任关系。其中0表示节点之间不存在信任关系,1表示节点之间具有完全信任关系。实际的Web服务推荐过程中,节点表示的Web服务是真实存在的,但Web服务之间的关系属性值却不容易获得。
对此这里选取Pearson系数作为信任网络模型的Web服务之间的信任值,该值可对Web服务之间的关系属性值进行直接表达:
(5)
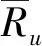
2 基于并行计算的Web服务推荐
2.1 基于两层受限玻尔兹曼机的Web服务质量预测模型
基于两层受限玻尔兹曼机的Web服务质量预测模型TLRBM被解释为具有对称连接的随机神经网络,其中图形模型中的节点由两层二进制变量组成。其中,隐藏层(h)表示对于不同服务用户具有不同QoS值的随机二进制特征,可见层(V)表示服务用户、Web服务项和QoS值,但存在问题是如何有效地处理缺失的QoS值。可见层通过对称加权连接与隐藏层连接。用Gibbs分布给出在可见层和隐层上的联合概率分布。
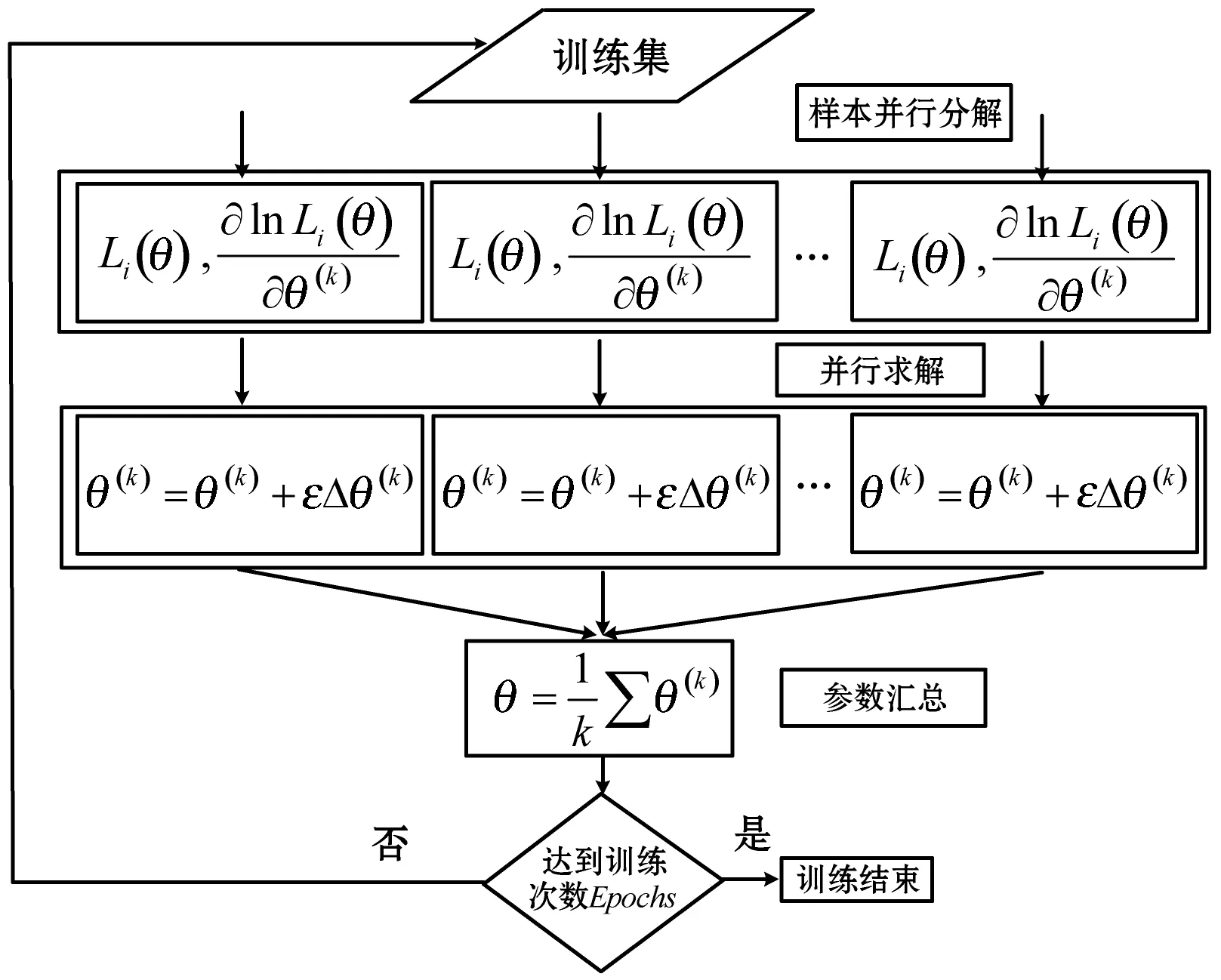
令V表示m个可见单元v1,v2,…,vm的向量,其由m服务用户和n个Web服务项目组成,称为用户项目矩阵。该矩阵ri,k中的每个条目表示服务用户i在Web服务项k上观察到的QoS值的向量(例如:响应时间、故障率等)。令F表示h个隐藏单元h=(h1,h2,…,hn)的数量,它可代表随机二进制特征,这些特征对于不同的用户具有不同的值。
每个服务用户被认为是TLRBM的一个单独的训练案例,它有一个对称地连接到一组二进制隐藏层的softmax可视层。然后,每个隐藏单元可以学习建模不同值之间的显著依赖关系。每个TLRBM都有一个单独的训练案例,但是所有相应的权重和偏差都被绑定在一起,因此如果两个用户具有相同的值,那么它们的两个TLRBM必须在该Web服务项和隐藏层的softmax可视层之间使用相同的权重。
根据图3所示模型,对每个观察可见层的列使用条件多项式分布softmax,对隐藏层用户特征h使用条件多项式分布。因此,可将式(2)和式(3)推广如下:
(7)
由于在一个层的变量之间具有独立性,因此可简单使用Gibbs采样进行数据采集,其具有并行采样特性。因此,Gibbs采样可利用以下两个步骤完成:基于p(h|v)对隐藏层的新状态h进行采样,以及基于p(v|h)对可见层的状态v进行采样。边际分布可以通过求和可见向量V的所有可能值进行计算:
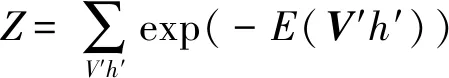
j=1,2,…,F
(9)
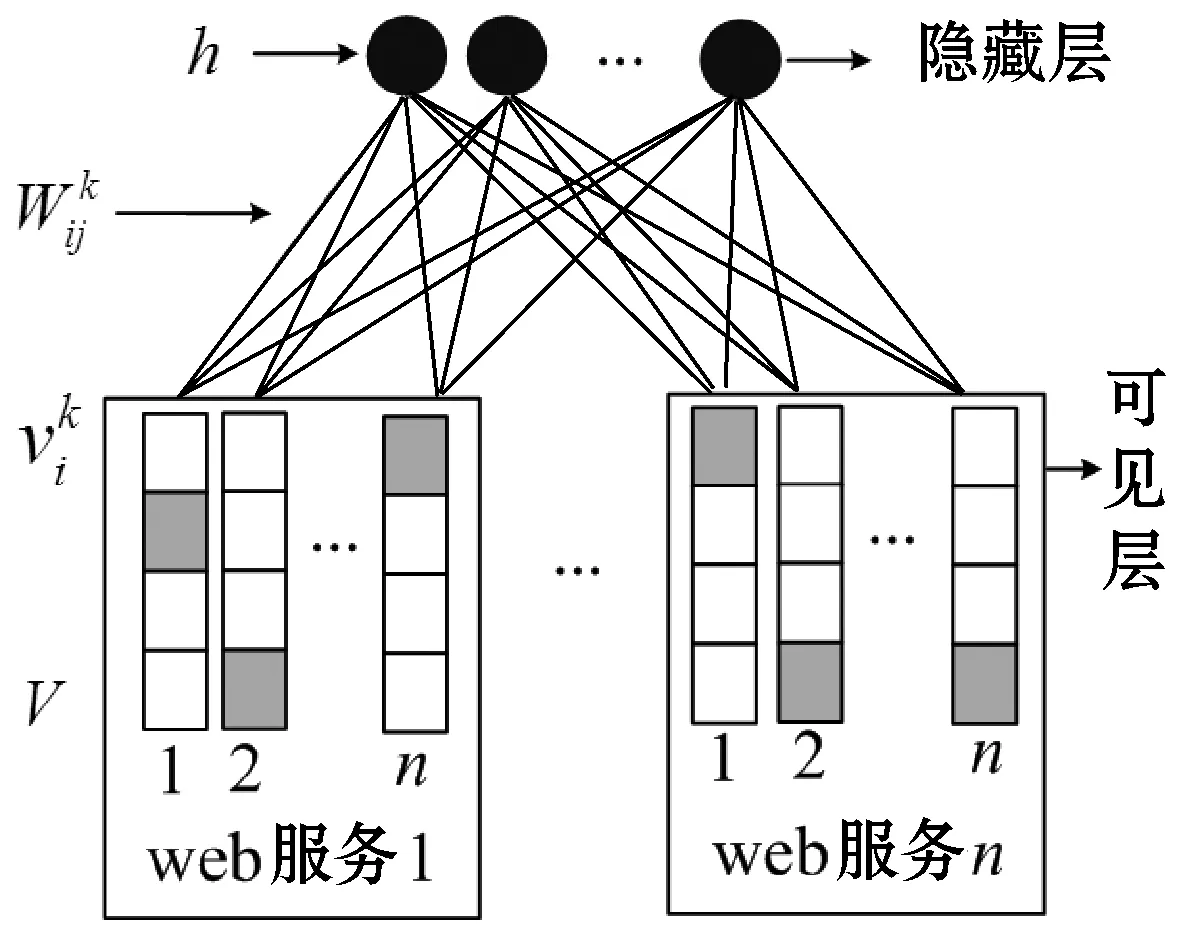
图3 基于两层受限玻尔兹曼机的Web服务质量 预测模型(TLRBM)
2.2 模型学习过程
首先,提出在无条件TLRBM模型中的学习方法。尽管与图1中的模型相比,TLRBM模型中的可见单元的激活功能已经改变,但是其对于式(4)的学习过程是一致的。唯一区别是Gibbs采样仅用于在非丢失的QoS值上重构分布。因此,可依据式(4)获得如下形式参数更新:
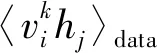
其次,学习条件TLRBM模型与基本模型相似。但是在条件TLRBM模型中,有一个额外的学习参数D:
ΔDij=ε(〈hj〉data-〈hj〉T)ri
(12)
参数Δci的更新公式为:
Δci=ε(〈vi〉data-〈vi〉recon)vi
(13)
再次,为了进行推荐,通过在softmax单元上使用推理过程来预测缺失QoS值,然后对所有缺失QoS值执行单个Gibbs采样步骤。给定可见向量V的值,可预测查询服务q的QoS值,其相对于隐藏层的数量具有时间线性关系:
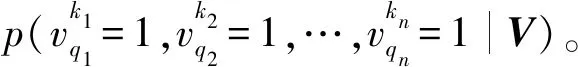
2.3 TLRBM服务推荐模型
如上所述,CD学习算法使用了运行吉布斯的样本分布,迭代(T步骤)直到收敛为止。使用称为动量法的启发式方法,其思想是在计算迭代t上的更新时考虑在迭代t-1处计算的更新,并且采取以下形式:
式中:a∈[0,1]。Web服务推荐的TLRBM模型算法学习过程见算法1所示。
算法1Web服务推荐的TLRBM模型学习过程
2. 令n=0,在时间n上计算预测误差En;
3. Repeat
4. for allS集内样本 do
5. for all当前样本中的udo
6. 基于可见层计算隐藏概率贡献累积:
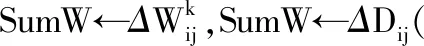
8. 计算隐藏状态的概率:
pj=p(hj=1|V,r)(参见式(14));
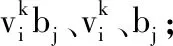
9. 吉布斯抽样:令T=0;
Repeat
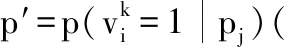
在开始另一次迭代之前计算误差;
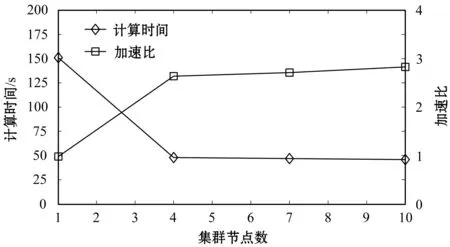
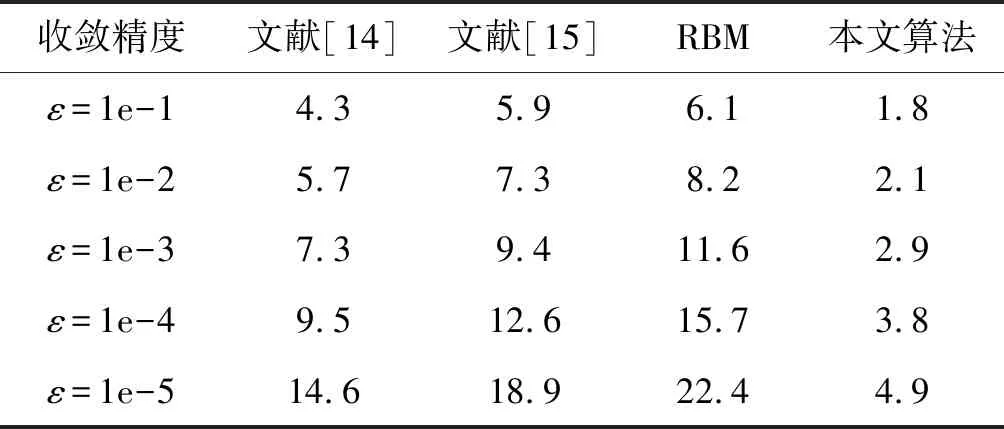
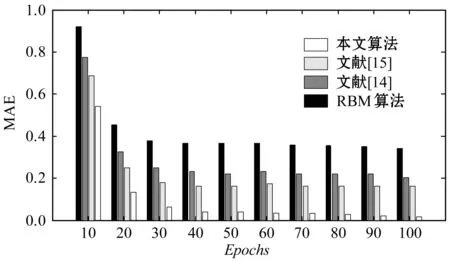
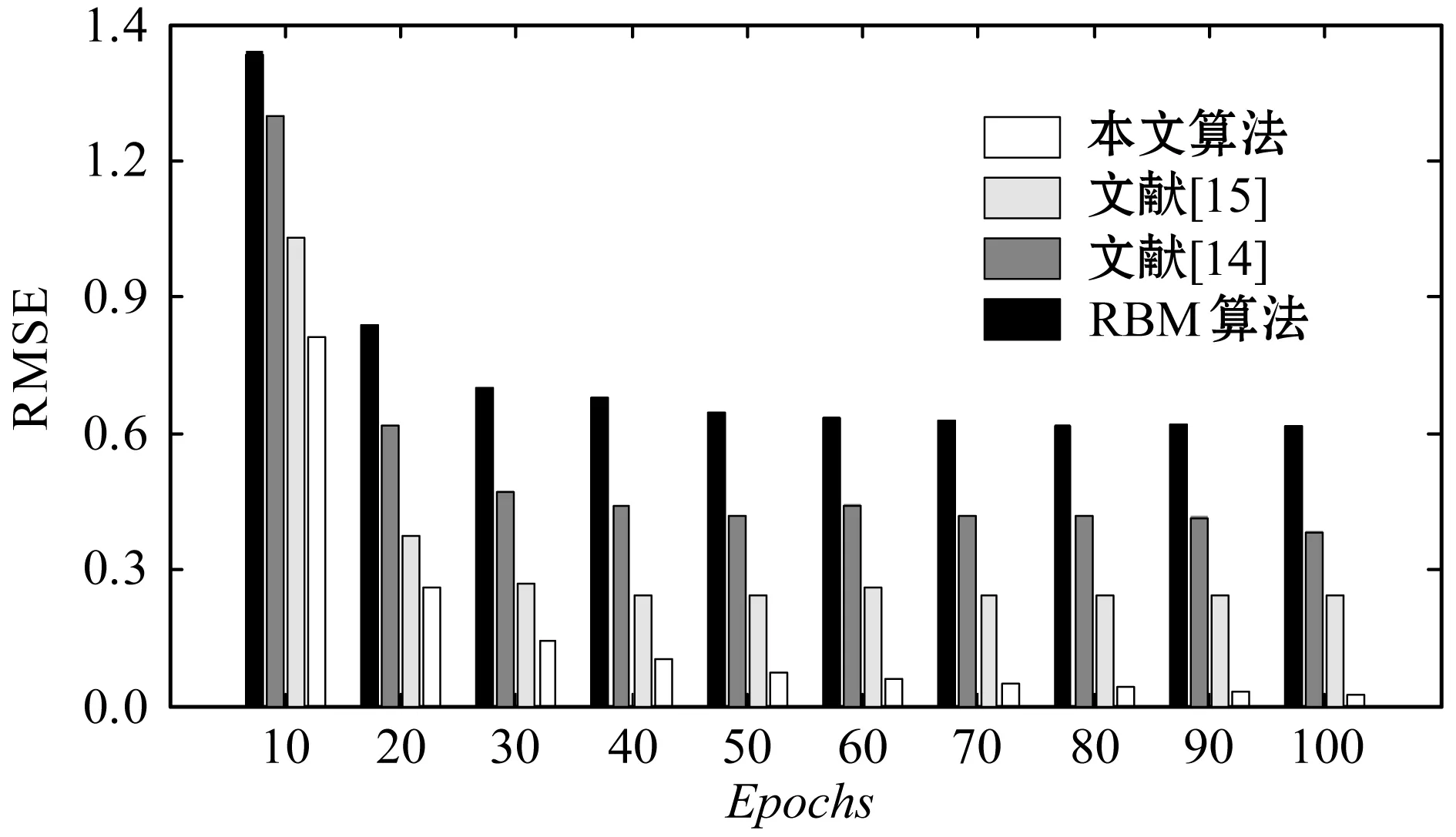
Until(++stepT 10. endfor 11. 对比贡献积累差异: 12. 更新权重及参数: 利用式(12)更新ΔDij; 利用式(13)更新Δci; 13. endfor 14.n++;在时间n上计算预测误差En; 15. Until(En-1-En)>ε; 随着现代互联网科技的快速发展,Web服务数量呈现出大幅度增长趋势,以面向Web的运行nginx系统的计算机数量为例,据相关统计,2010年大约有不到5万台数量,2014年的数据大约在40万台左右,而到了2017年,数量则大幅度增加到140万台左右,增长速度呈现出加速增长态势。但是,目前采用单线程处理方式进行Web服务推荐已经无法与现代Web服务推荐应用实际相适应,算法的执行效率受到很大的制约。Spark并行化模型是一种采用内存计算方式的系统,其具有开源属性便于开发利用,目的是实现大型数据并行化处理。Spark采用的是一种具有分布式结构的弹性数据结构,可将中间计算数据在内存中以缓存形式进行存储,从而省去了中间硬盘读取环节,便于计算速度的提升。 图4 基于Spark并行化实现 为验证所提算法的性能,选取Epinions数据集作为实验对象,该数据集由Massa等通过爬取技术在Epinions网站上获得的Web服务数据,共含有401 593个Web服务在139 528个项目上的测评结果,参见文献[13]。设置数据集中前80%的Web服务数据构建算法模型的训练集,剩余的20%Web服务数据构建算法模型的测试集。对Epinions中的Web服务数据进行优化处理,对于不存在关联属性的Web服务数据进行删除,可得到具有31 932个Web服务在78 893个项目上的测评结果。 实验过程中,设定RBM模型中隐藏单元的节点数量为160,模型训练过程的迭代次数上限是Epochs=100或者收敛精度设置为ζ=1e-5。实验硬件配置:CPU为i5-6400k 3.0 GHz,内存是金士顿ddr3-1600K,系统为Windows 10旗舰版,仿真平台选取MATLAB 2013a。 当前Web服务推荐系统中大多使用推荐精度作为算法推荐效果的评价指标,其定义为模型评价结果与用户真实评价结果之间的误差均值绝对值指标(MAE指标),或是根均方误差指标(RMSE指标)。其中,MAE指标主要评价计算推荐结果与用户真实评价结果的误差均值: (16) 另一评价指标RMSE指标的具体定义如下: 选取集群节点的数量作为评估参数,考察集群节点数量变化对于算法计算性能的影响。集群节点的数量的变化区间是[1,10],评价指标选取算法计算时间和加速比两项指标,实验结果如图5所示。 图5 集群节点数实验影响 根据图5所示实验结果,横坐标为实验选取的计算集群节点数量,纵坐标是算法运行时间或计算加速比。根据实验结果可知,随计算节点数量的增加,算法的计算时间呈现出单调下降趋势,而计算加速比则呈现出单调加速趋势。同时也可看出,随着集群节点数量的增加,算法的计算时间降低幅度和加速比增加幅度逐渐趋缓,主要原因是随着节点的增加,节点之间的通信开销逐渐增加,导致算法的计算性能增加幅度受到制约,因此对于本文选取的实验对象选取计算节点为4是最为合适的设置方式。 下面,对算法的推荐精度和计算效率性能进行对比实验,对比算法选取:文献[14]、文献[15]以及未采用Spark并行化实现的受限玻尔兹曼机算法(RBM)。表1给出选取不同收敛精度情况下算法的计算效率对比情况。 表1 计算效率对比 ×10 s 根据图5实验结果,本文算法选取集群节点数为4,另外,这里选取的收敛精度指标并不是式(16)-式(17)所定义的MAE和RMSE指标,而是式(9)所定义的能量函数指标。 根据表1结果可知,随着收敛精度设定参数的增加,集中算法的计算时间均呈现出增加趋势,因为收敛精度越高算法收敛过程所需的迭代步数越多,因此计算时间越大。同时,在几种算法对比中,本文算法的计算时间最少,这是因为采用了并行计算方式,实现了多个计算节点的并行执行,因此本文算法更加适用于互联网大量服务推荐过程,并且对于不同的数据流,可通过扩展集群节点方式进行计算性能改善,具有更高的可扩展性和更高的实际应用价值。 设置迭代次数上限是Epochs=100,文献[14]、文献[15]、RBM算法以及本文并行算法的MAE和RMSE指标的实验结果如图6和图7所示。 图6 MAE指标对比结果 图7 RMSE指标对比结果 根据图6-图7实验结果可知,随着迭代次数增加,几种算法的MAE指标和RMSE指标均呈现出逐渐收敛趋势。从收敛精度和速度上看,本文算法的Web服务推荐性能要显著优于文献[14]、文献[15]以及RBM算法的推荐性能。另外,文献[15]优于文献[14]和RBM算法的推荐性能。其中RBM算法的推荐性能最差,收敛速度非常缓慢,这也从侧面印证了本文采用的Spark并行化实现方式的有效性。 本文提出一种Spark框架实现的基于两层受限玻尔兹曼机Web服务受限玻尔兹曼机推荐模型,主要贡献如下:(1) 引入一种新的模型,通过有效的学习和推理过程从服务提供者和客户端可实现Web服务QoS的实时监控。(2) 为了有效地处理大数据集,采用了CD学习来提高收敛时间,特别是提出采用Spark并行化实现算法的有效拓展。下一步研究方向,主要是基于所提TLRBM模型,完成不同业务用户QoS值信息采集以及主动用户QoS预测系统的构建。2.4 基于Spark并行化实现
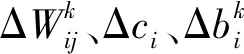
3 实验分析
3.1 实验设置
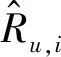
3.2 结果分析
4 结 语
