一种基于网格划分的密度峰值聚类改进算法
2019-08-14江平平曾庆鹏
江平平 曾庆鹏
(南昌大学信息工程学院 江西 南昌 330031)
0 引 言
聚类分析作为数据挖掘技术中有力的工具之一,其应用范围普及较广,关联机器学习[1]、模式识别[2]、数据分析、图像处理和市场研究[3]等多个领域。聚类分析的目是将有差异的对象集合划分到不同的类或簇中,相似对象的集合划为同一类,且不同类中的对象差别较大[4]。
聚类算法大体上可分为:基于划分的方法[5-10];基于层次的方法[11-12];基于密度的方法如DBSCAN[13]、GDBSCAN[14]和OPTICS[15]等;基于网格的方法如STING[16]、WavcClustcr[17]和Clique[18]等;基于模型的方法[19]等。不同的聚类算法各有其优缺点,如基于密度的DBSCAN算法具有处理任意形状的簇类以及对噪音点进行过滤等长处,然而该算法需耗费大量时间和空间对距离矩阵进行计算,且对输入参数较为敏感。因此,各学者提出了众多改进方法[20-23]。文献[20]和文献[21]对半径参数进行自适应改进,但领域密度阈值仍需靠经验方法选取;文献[22]解决的参数选择困难的缺陷,但时间开销较大;文献[23]提高了运行效率,但对于多维数据集的处理存在局限性。
Alex Rodriguez和Alessandro Laio于2014年在《Science》杂志上发表的基于密度峰值聚类算法DPC[24]能
够处理任意形状的簇、能将数据点准确归类,并除去噪声点。然而该算法时空复杂度高,且对一些较为复杂的数据集,难以准确地依据决策图人工选取聚类中心。
针对DPC算法聚类时空复杂度高,无法有效处理大数据集且需人工选取聚类中心的问题。本文提出一种改良的基于网格的密度峰值聚类算法,先对网格代表点进行聚类,自动确定聚类中心;之后将非核心代表点和各网格中数据点进行归类;最后对边界的代表点和噪声点进行处理完成聚类。
1 DPC算法
快速搜索和发现密度峰值聚类算法DPC的聚类中心具有两个特征:1) 数据点自身的局部密度大;2) 局部密度大的点相对之间的间隔较远。对于各数据点xi皆需计算其局部密度ρi以及高局部密度距离δi,通过这个两个值来构建决策图[24],人工选取ρi和δi相对大的点作为聚类中心,然后将其他数据点归类并剔除噪声点。
定义1局部密度:一个数据点一定半径内其他点的个数。点xi的局部密度ρi为:
式中:dij=dist(xi,xj)代表xi和xj的距离,dc为所有样本点间距离的最小2%的距离中的最大距离。函数χ(x)定义如下:

当数据点为连续时,局部密度ρi为:
式中:参数dc>0,为截断距离,需要人工指定。
定义2高密度距离:比自身局部密度高的点中,与离自身最近的那个点之间的距离。对于任一点xi的高密度距离δi为:
式中:对应指标集IS定义为:
DPC算法特征值ρi和δi画出决策图,人工选出这两个数值都相对较高的数据点作为聚类中心,将剩余点按局部密度倒序排序,依次归入局部密度更大且距离最近的数据点所在类中。
定义3边界点:如果一个已分配的数据点与其他类中的点的距离在阶段距离dc内,则该点为边界点。
DPC算法的最后一步是对边界点的处理,利用密度参数dc算出类边界点集,然后指定边界点集中密度最高点的密度值作为划分核心点和噪音点的阈值。DPC算法步骤:
(1) 初始化参数dc;
(2) 根据式(1)计算数据点的局部密度ρi;
(3) 按局部密度ρi倒序排序;
(4) 根据式(4)计算数据点的相对距离δi;
(5) 构建基于ρi和δi的决策图,并手动选取聚类中心点;
(6) 将剩余非聚类中心点归类;
(7) 对边界点处理,检测噪声点。
DPC算法具有可发现非球形簇,所需参数少,无需进行迭代等优点。然而该算法同时也存在处理大规模数据集时运行时间过长,耗费内存空间过大,人工难以准确地选取聚类中心等缺陷。
2 基于网格划分的密度峰值聚类算法(G-DPC)
针对DPC算法时空复杂度高以及人工选取聚类中心易造成偏差的问题,本文提出了一种改进的基于网格划分的密度峰值聚类算法G-DPC。
2.1 网格划分
定义4网格边长:假定存在一个d维数据集X={x1,x2,…,xn},n∈N+,xi∈Rd。属性(A1,A2,…,Ad)都是有界的,设第i维上的值在范围[li,hi)中,i=1,2,…,d,则S=[[l1,h1)×[l2,h2)×…×[ld,hd)]即是d维数据空间。将数据空间各个维度划分成均等且不相交的网格单元[25-26]。网格边长side计算公式为:
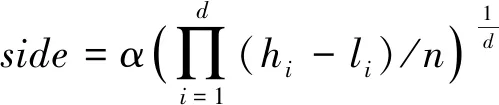
式中:ɑ为控制参数,网格划分边长side的取值会对数据聚类的效果造成影响,太大会降低聚类精度;太小则影响处理速度。当ɑ∈(0,2]时,算法的聚类效果较好。本文实验中选取ɑ值为1.5。
例1:图1为Birch3[27]的原始数据集分布情况,若依照式(6)对该数据集进行网格划分,划分后如图2所示,将网格单元点的统计信息取代原先的数据点,从而实现数据压缩的效果,利于选取聚类中心。
图1 Birch3的数据分布

图2 网格划分后的数据分布
2.2 数据聚类
2.2.1自动选择聚类中心
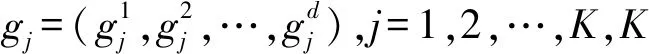
网格j中点的集合为P={p1,p2,…,plj},lj为该网格j内数据点的总个数。则该网格的代表点为:
定义6代表点局部密度值:网格代表点Pj的局部密度是网格j内数据点的个数,网格j中点的个数为:
式中:
则网格代表点Pj的局部密度为ρj=lj。
定义7代表点高密度距离值:以网格代表点Pj更高密度代表点Pk的最近距离,作为网格代表点Pj的距离值,记为δj。
式中:Dkj是网格代表点Pk与网格代表点Pj的距离。
在选取聚类中心时,文献[24]采取对决策图进行观察后再由人工选择中心的方式,筛选局部密度和高密度距离值均较大的点作为聚类中心,这种方法在处理数据分布差距大的小规模数据集时较为简单,然而在处理大规模数据集时,如图3所示,决策图中点的分布差距不明显时便难以准确选择聚类中心的数目。
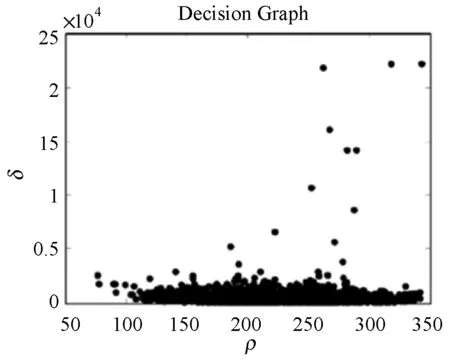
图3 DPC算法决策图
为解决上述问题,众多学者提出了解决方案,例如,文献[28]中的Fuzz-CFSFDP算法使用基于上模糊规则自适应地选择集群中心,然而该算法同样对参数dc的取值敏感,数据集的测试精确度较低;文献[29]中采用根据簇中心权值的变化趋势的算法来寻找聚类中心,该方法虽能有效避免手动选取聚类中心带来的误差,但只适用于低维数据集分析。本文给出一种改进自适应的方法,无需人工干预选择确切聚类中心的数量。其判定函数为:
ρCi-μ(ρi)≥0
(12)
(δCi-E(δi))/2≥σ(δi)
(13)
式中:ρCi是聚类中心网格代表点的密度,μ(ρi)是所有网格代表点密度的均值,δCi是同一个类簇中网格代表点距聚类中心代表点最小的距离,E(δi)是所有δi的期望。式(12)表示该网格代表点的局部密度值大于所有网格代表点局部密度的均值,这样的判定方法满足密度峰值算法中聚类中心往往分布在相对高密度区域这一条件;式(13)的判定方法满足聚类中心间的相对距离较远这个条件。
因此,当网格代表点对象符合以上两个公式条件时,将该网格代表点选定为聚类中心。
2.2.2数据点归类
本文采用原DPC算法中的最近邻算法对剩余数据点进行归类。在完成聚类中心代表点的选择之后,将剩下的非聚类中心代表点按照ρi降序分类到距其最近且局部密度大于该点的代表点所在类中,并将原数据集中的数据点归属到其网格代表点所在类中。
2.3 边界点与噪声点的处理
本文G-DPC算法中,边界点的对象是符合定义3的网格代表点。首先根据密度参数dc计算出当前类簇中边界网格代表点的集合,在边界点集中找出拥有最高密度的网格代表点,将该代表点的密度作为阈值以划分出核心代表点和噪声点,保留密度大于等于该密度阈值的代表点作为簇内核心代表点;剔除当前类别中小于此密度阈值的噪声代表点,同时将该噪声代表点所在网格中的数据点也一并剔除。
2.4 算法实现
G-DPC算法实现的具体步骤如下:
(1) 将数据集标准化处理;
(2) 依据式(6)计算出网格划分参数side,将数据空间划分为均等且不相交的网格单元;
(3) 将数据点映射至相应的网格单元中,由式(7)和式(8)求出各网格的代表点,并统计每个网格中分别所含数据点数目;
(4) 根据式(9)和式(10)计算网格代表点Pi的局部密度ρi;
(5) 计算网格代表点之间的距离矩阵Dij,并求出密度参数dc;
(6) 将网格代表点按ρi进行倒序排列,由式(11)计算各网格代表点的高密度距离δi;
(7) 由式(12)和式(13)自适应确定聚类中心代表点,按照ρi降序分类到距其最短的且局部密度大于该点的网格代表点所在类中,将原数据集中所有数据点归类到其所在网格代表点所属类中;
(8) 由密度参数dc计算出当前类的边界点集,选出边界点集中密度最大的代表点,并将该点的密度作为划分当前类的核心代表点和噪声点的阈值,剔除当前类别中小于此密度阈值的代表点及代表点所在网格中的其他数据点;
(9) 返回最终聚类结果。
2.5 高维数据降维方法
降维是处理高维数据的一种有效方法,降维技术分为线性降维和非线性降维。线性降维方法主要有主成分分析(Principal Component Analysis,PCA)和多维尺度分析(Multi-Dimensional Scaling,MDS)[30]等;非线性流形降维方法主要有等距映射(Isomap)[31]、局部线性嵌入(Local Linear Embedding,LLE)[32-33]和拉普拉斯特征映射(Laplacian Eigenmaps,LE)[34]等。与传统的线性降维方法相比,非线性降维方法能更有效地发现复杂高维数据内嵌的低维结构。
本文采用LE方法进行降维,该方法用局部的角度去构建数据之间的关系。其主要思想是高维空间中距离近的点投影到低维空间后距离也应尽量接近。
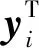
定义对角矩阵D,对角线上(i,j)位置元素等于矩阵W的第i行之和,经过线性代数变换,上述优化问题可以用矩阵向量形式表示如下:
mintr(YTLY) s.t.YTDY=1
(15)
式中:矩阵L=D-W是图拉普拉斯矩阵。限制条件YTDY=1保证优化问题有解,并且保证映射后的数据点不会被“压缩”到一个小于m维的子空间中。算法具体步骤如下:
(1) 使用K最近邻方法构建稀疏邻接图,若i在j的k个最近邻之中,则i和j有边,否则无边;
(2) 采用直接映射方法为每条边赋值权重。若i、j相连,则wij取值1,否则为0;
(3) 通过式(16)计算拉普拉斯矩阵L的特征向量与特征值:
Ly=λDy
(16)
式中:D是对角矩阵,满足式(17)和式(18),选择最小的m个非零特征值对应的特征向量作为降维后的结果输出。
L=D-W
(18)
2.6 聚类效果评价指标
本文通过聚类精度(Accuracy)和归一化信息熵(Normalized Mutual Ingormation,NMI)两种聚类评价指标来检测G-DPC算法的聚类效果。同时,也将该算法与其他算法的运行时间对比作为聚类效率的主要评价指标。此外,还通过对算法的时间复杂度和空间复杂度进行探讨以分析算法效率。
(1) Accuracy作为聚类效果的评价指标,其公式如下:
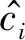
(2) NMI评价标准通过计算聚类结果与真实类别标号之间的互信息来评价聚类结果与真实类别标号的一致性[35],其公式如下:
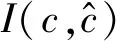
3 实验仿真
3.1 数据测试
本文实验所采用的计算机硬件配置为Intel Core i7处理器(主频3.4 GHz)、16 GB内存;实验的软件环境为Windows10操作系统,采用MATLAB编程实现本文算法。
本实验选取两组数据集进行测试。
第一组采用六个不同数据量且维度都为2的低维人工数据集,主要用来分析随着数据量的增加,G-DPC算法与DPCA算法、DBSCAN算法以及GRIDBSCAN算法的时间效率。其中Compound[36]、Aggregation[37]、unbalace[38]、D31[39]、t4.8k[40]为小规模数据集,Birch3[41]为较大规模数据集,共有10万条。实验中关涉的相似度矩阵计算均采取欧几里得方法。各数据集的详细信息及实验对照结果如表1所示。
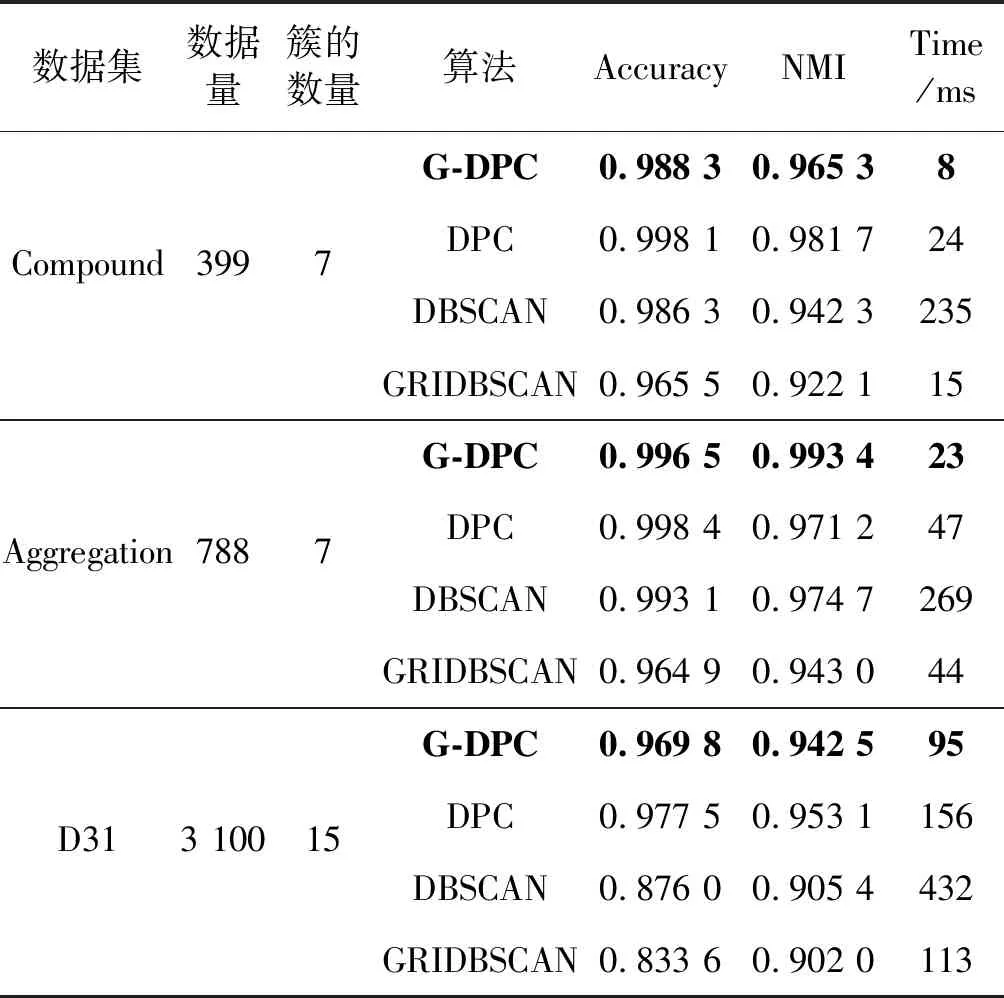
表1 低维数据集算法效果对比
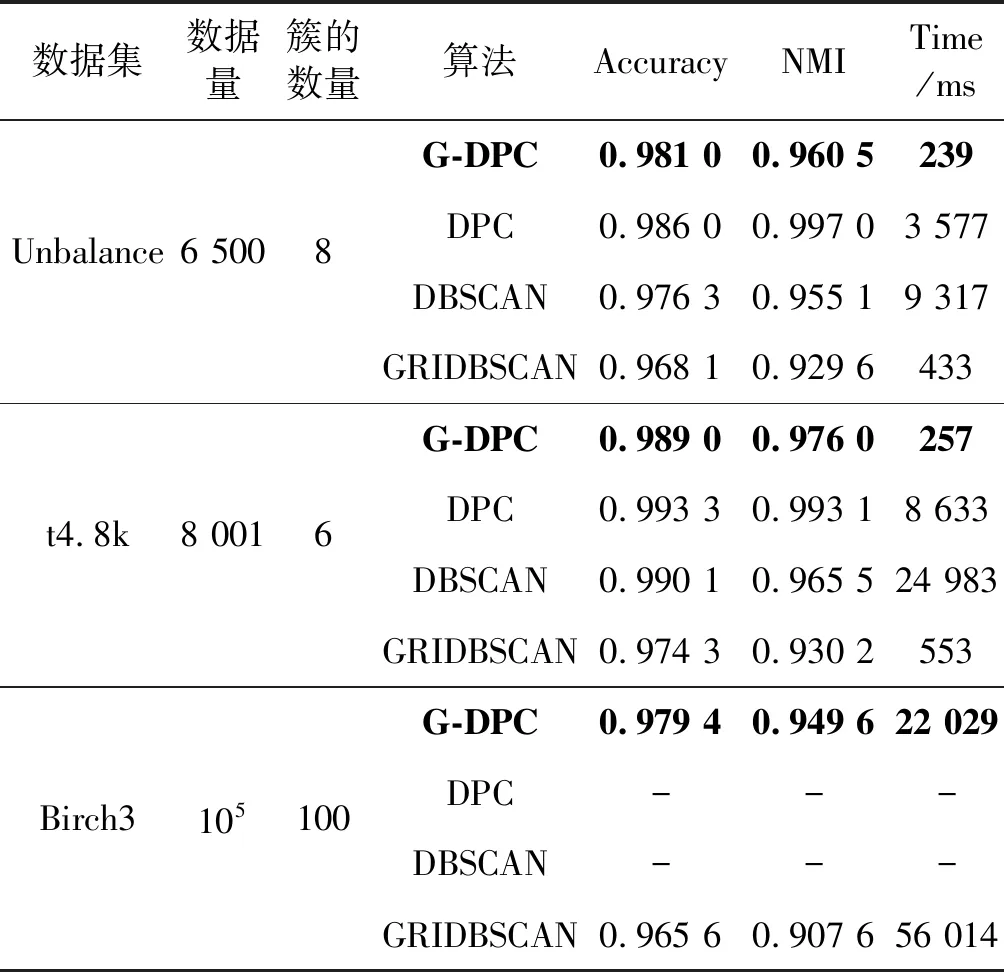
续表1
为了更直观地对比DPC算法和G-DPC算法DPCA算法、DBSCAN算法以及GRIDBSCAN算法的效率,通过表1数据给出了几种算法的运行时间和精确率对比图,如图4和图5所示。因Birch3数据集过大,DPC算法运行过程中内存溢出而无法完成聚类,所以只对前五个数据集进行可视化。
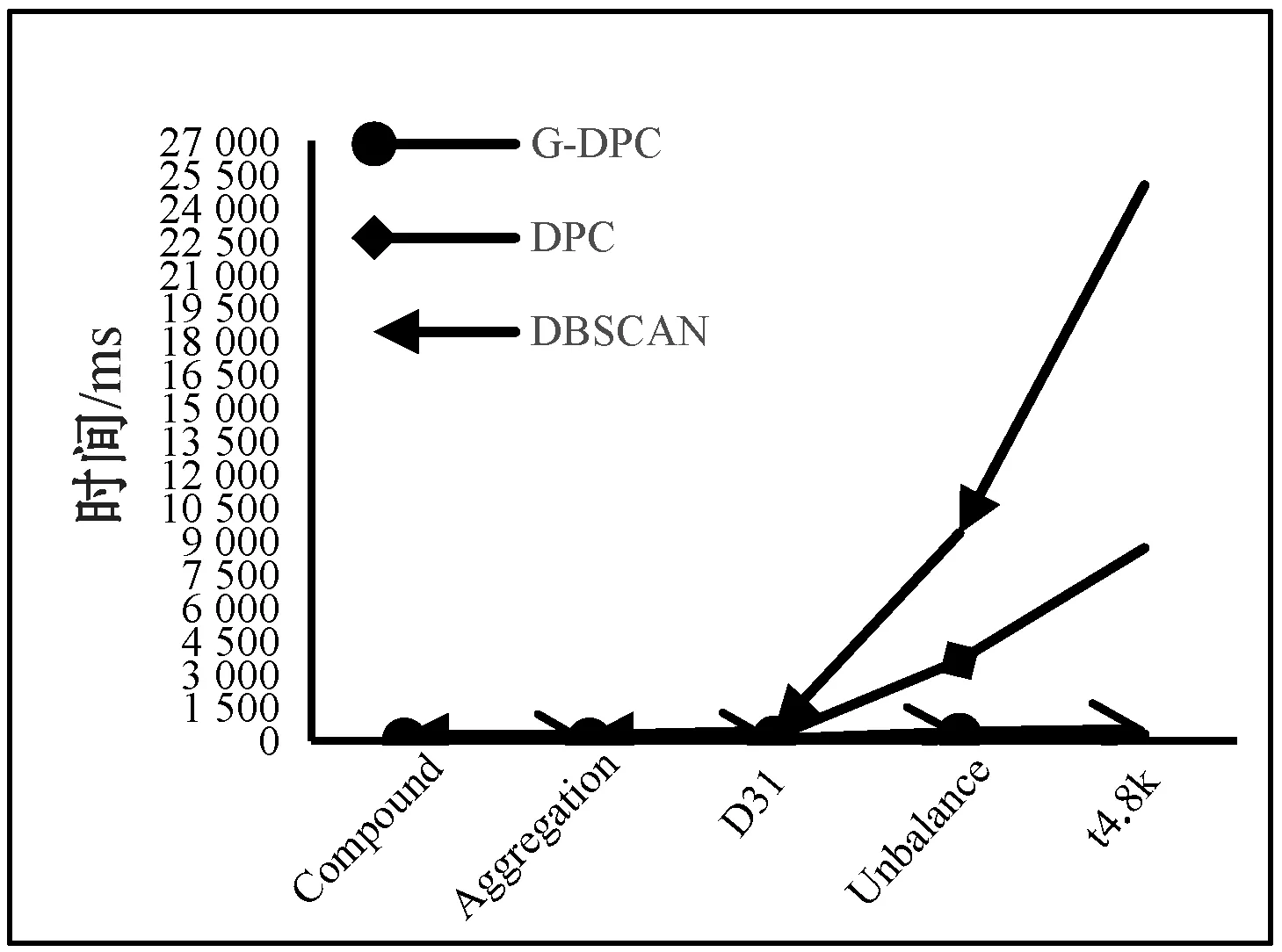
图4 低维数据集的算法运行时间对比
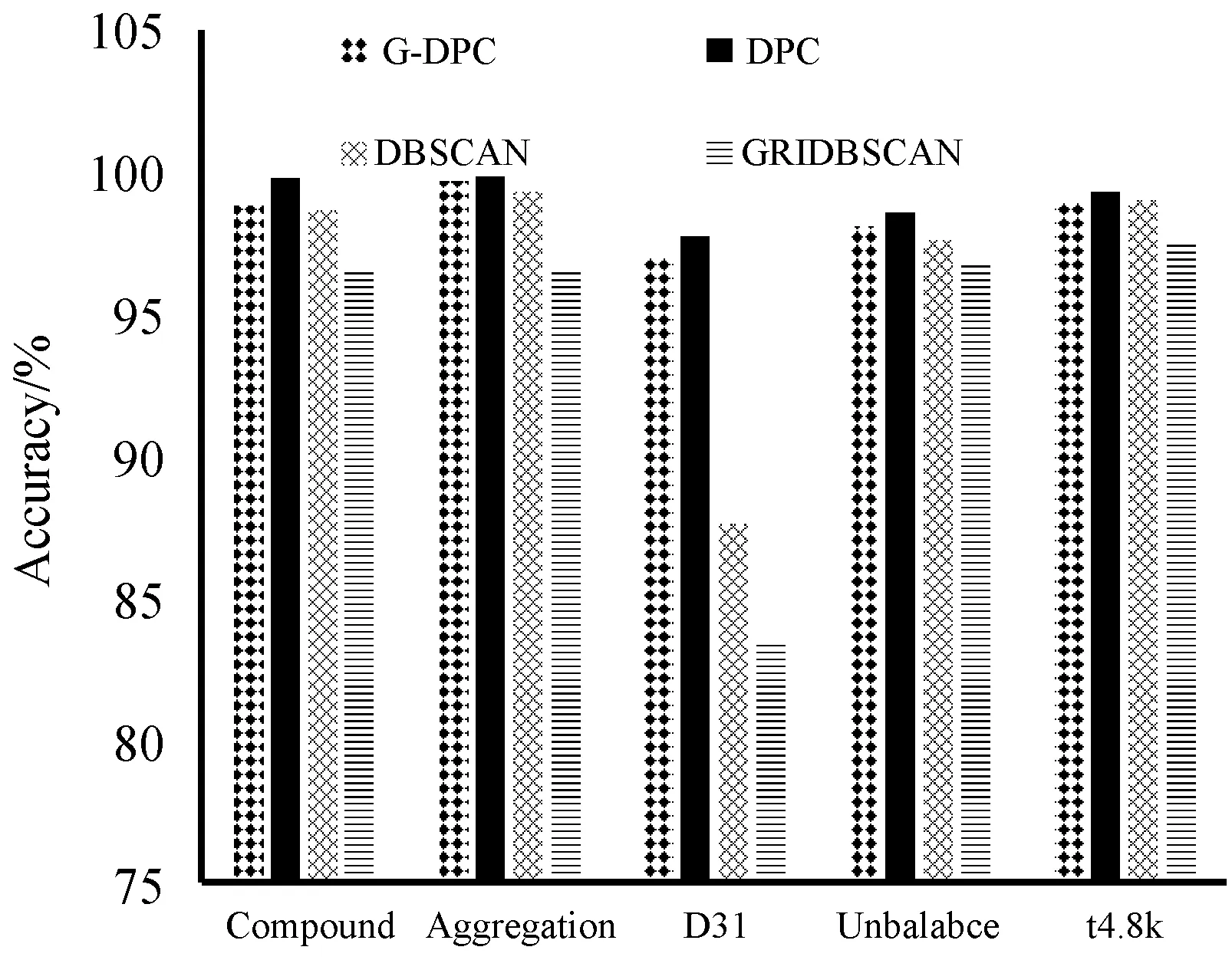
图5 低维数据集的精确度对比
通过表1、图4和图5可以得出,DPC算法和DBSCAN算法随着数据量的增加算法开销的时间成指数型增长,而本文的G-DPC算法时间增长和数据量成线性关系,且比GRIDBSCAN算法更快。
图6为G-DPC算法在数据集Birch3上的聚类效果图,聚类结果基本符合图1中的数据分布情况。因此本文中算法在处理大范围数据集上有着明显的优势,由于是基于网格的算法,在精确度指标上稍逊于DPC算法,但是差距很小,总体效果依然优异。
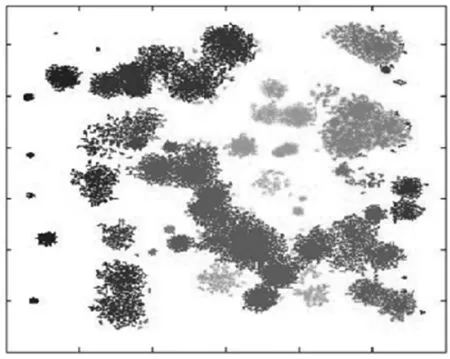
图6 Birch3数据集聚类结果
第二组数据采用UCI公共数据集中的Iris、seeds、wine和ring四个高维数据集对G-DPC和DPCA算法、DBSCAN算法以及GRIDBSCAN算法进行试验,采用拉普拉斯特征映射方法降维,并对照几种算法对高维数据的运行效率。各数据集的详细信息如表2所示,图7和图8分别为各算法的运行时间对比图以及精确率对比图。
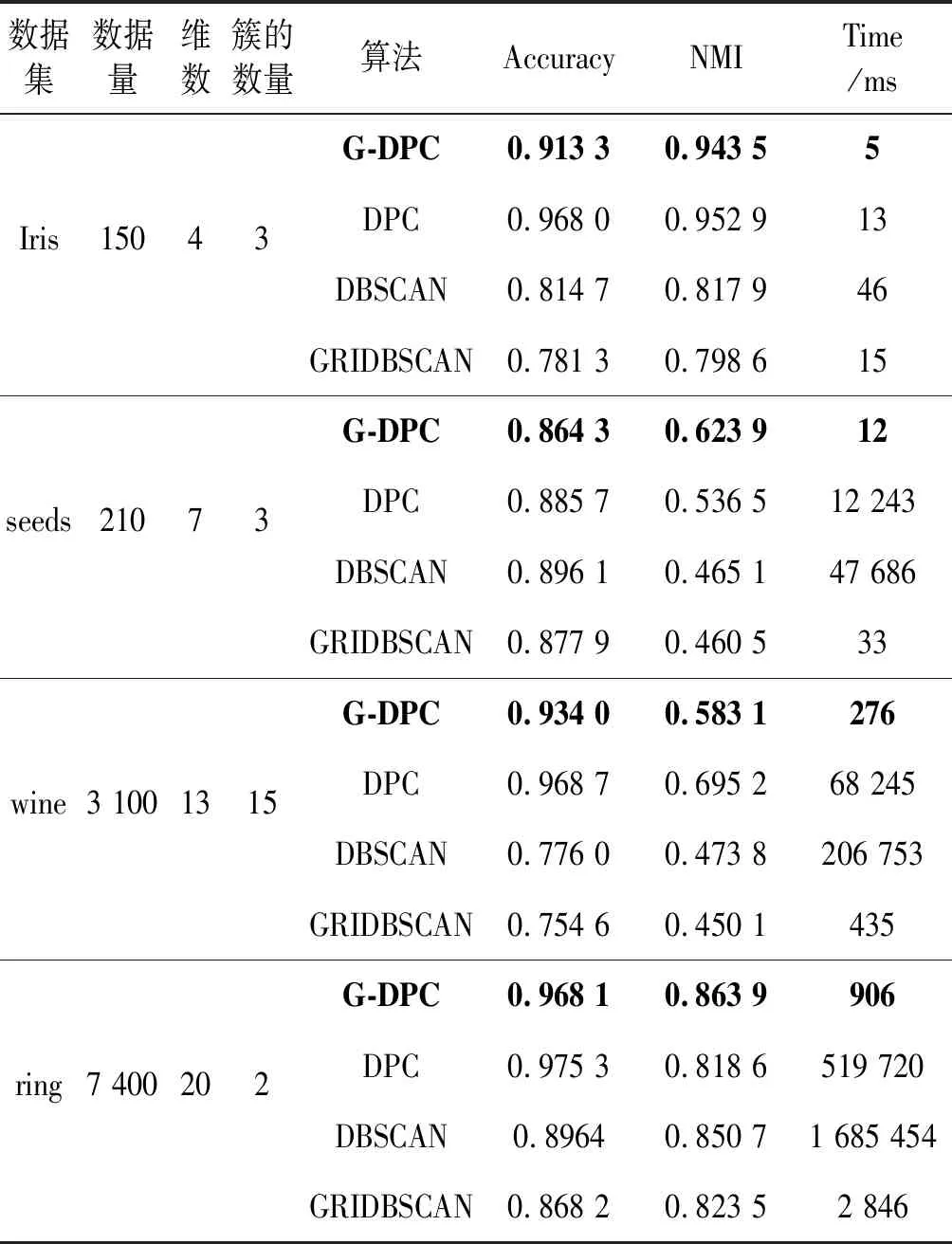
表2 高维数据集信息
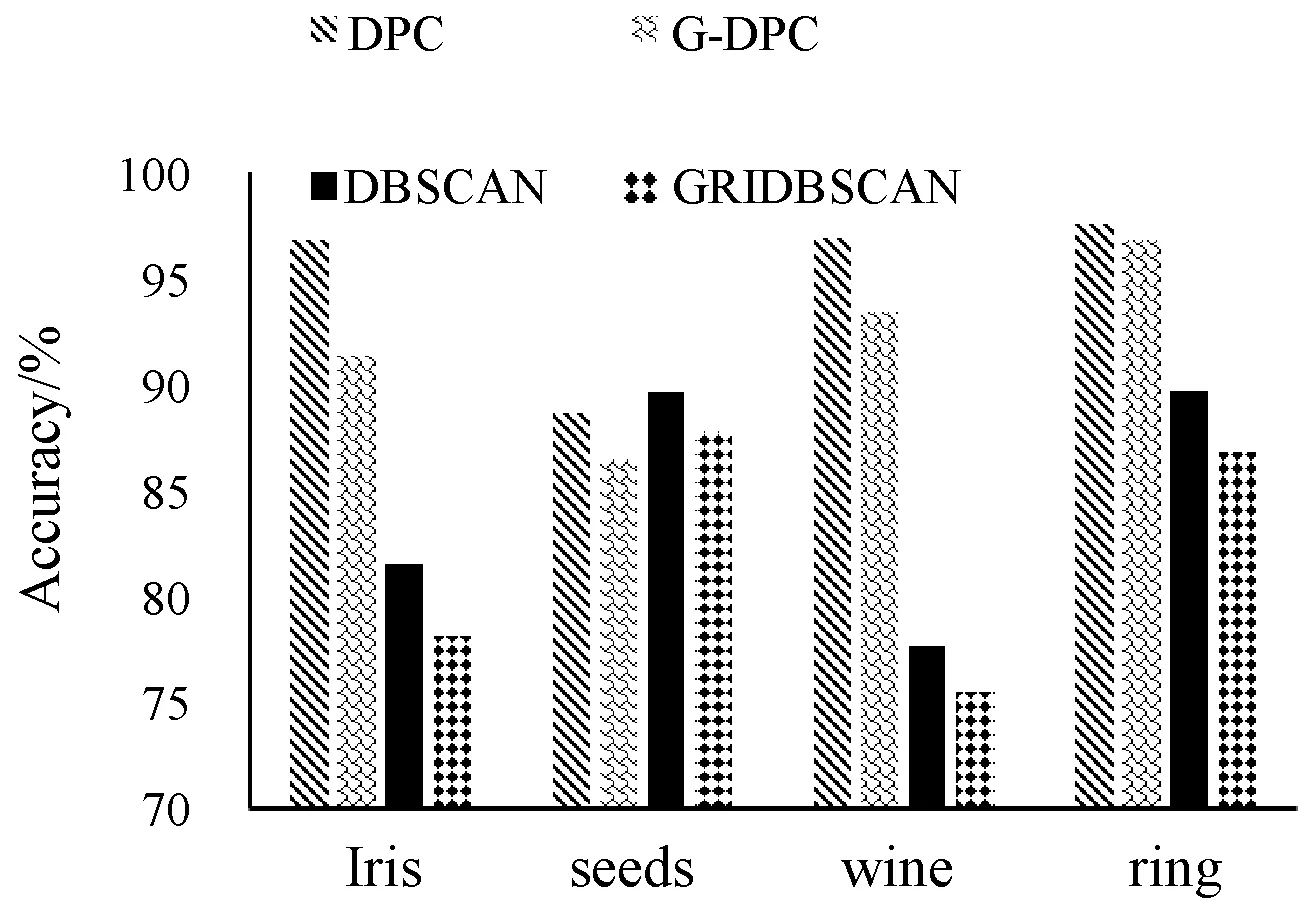
图7 高维数据集精确度对比图
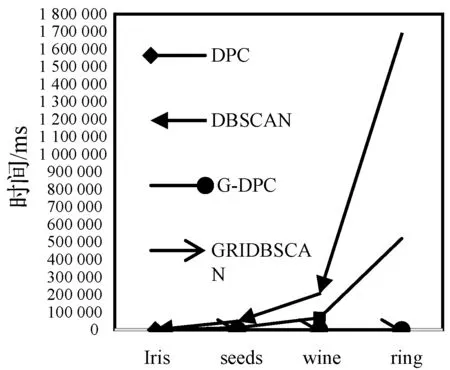
图8 高维数据集的算法运行时间对比
由图7和图8可以看出,G-DPC算法在高维数据集上聚类精度相较于低维数据集略低,但总体来说聚类效果依然良好。在精确度指标上,G-DPC算法和DPC算法结果相差不大,聚类质量基本持平,均远高于DBSCAN算法和GRIDBSCAN算法。而在对高维数据集处理的时间效率上G-DPC算法远远优于DPC算法。
由上述实验可得,G-DPC算法极大地减少了内存和计算的开销,降低了时空复杂度,提升了运行速度。虽然该算法因为基于网格划分而对噪声点的处理较为敏感,精确率略有偏差,但并不影响总体效果。
3.2 算法分析
本文提出的G-DPC算法在时间上的开销包括网格划分、数据聚类、数据点归类和边界点处理共四个部分。其中:网格划分包括数据点映射至相应网格,和对网格单元信息的统计,时间复杂度为O(n);数据聚类的过程中耗费的最大时间代价为各网格代表点距离矩阵的计算,时间复杂度为O(k2);数据点归类是先将非核心代表点归类到核心点,时间复杂度为O(k2),其次将网格中的数据点归入其代表点所属类中,复杂度为O(n);对边界点的处理是先找到每个类中的边界代表点集,选出其中最高密度代表点密度作为阈值划分核心点和噪声点,时间复杂度为O(bk),其中b表示边界点代表点的个数。因此G-DPC算法的时间复杂度为:
Tall=2×O(n)+2×O(k2)+O(bk)
(14)
而原始的DPC算法在时间的开销上包含数据点之间的距离矩阵的计算,寻找聚类中心和非聚类中心的归类,所耗费的时间复杂度为O(n2)。
空间复杂度方面,G-DPC算法将数据点映射到k个网格单元中(假设为理想状态,数据均匀划分),其空间复杂度为O(k2),而原DPC算法中构建距离矩阵的过程与数据总数有关,其空间复杂度为O(n2)。
4 结 语
DPC算法需人工指定聚类中心个数,对数据对象距离矩阵的计算需耗费大量的时间和空间,限制了对大规模数据集的处理。本文基于网格聚类的思想进行网格划分,用网格代表点替代网格单元整体,从而减少计算次数。然后对各代表点进行聚类,大大降低了距离矩阵计算的时空复杂度,通过自动确定聚类中心的方法降低了人工取值带来的误差。在多种标准数据集的实验结果验证了G-DPC算法对大小规模数据集进行聚类的有效性。
