热点词汇的最长时间区间查询算法

路 畅 何震瀛 荆一楠 王晓阳

1(复旦大学计算机科学技术学院 上海 201203)2(上海市数据科学重点实验室(复旦大学) 上海 200433)3(上海智能电子与系统研究院 上海 201203)

0 引 言

高效、快速地获取热点词汇在新闻话题追踪[1]、金融市场分析[2]、商业智能[3]以及社会舆情监测[4]等领域发挥着重要作用。作为话题检测与追踪的核心任务之一，热点词汇(以下简称为热词)提取是当前的一个研究热点。

对语料库中的关键词及包含关键词的短语、句子进行聚类，是提取热点话题的一个重要手段。但在实际应用中，为了了解不同约束条件下的热词情况，用户经常查看不同过滤条件下的热词，以了解不同时间区域内的热词。因此，对关键词提取方法的效率进行优化，能有效提高热词检测的效率。

针对热词提取，业界已开展了大量研究工作。Krulwich等[5]利用启发式规则抽取文档中重要的词和短语。Salton[6]提出了TF-IDF算法，刻画了词汇对于语料库或其中一份文档的重要性。Bun等[7]改进了TF-IDF算法可能将更高的权重赋予语料库中出现较少的词汇的不足，提出了TF*PDF算法，将更高的权重赋予出现在多个文档中的词汇，以提取整个语料库的关键词和热点话题。迟呈英等[8]引入了话题权重，并将其与TF*PDF结合，以更全面地反映话题的热度分布情况。赵志洲等[9]提出了EHWE算法，对数据进行划分，在一定程度上优化了TF*PDF的计算过程。但是这些算法的一些共同不足是：

① 仅考虑整个语料库在某个时间区间关键词，未考虑不同偏好的用户对不同类别新闻等的查询需求。

② 面向挖掘任务，时间复杂度较高，当用户不断地更改查询条件(类别和时间区间)时，算法需要对词频和包含关键词的文档数进行重复计算，无法满足用户对于关键词提取的在线查询的需求。

在实际应用中，为了进行新闻追踪，用户需要对一组特定的词汇进行查询，以寻找这组词汇能够成为热点词汇所处的最长时间范围。这要求算法不断地更新查询条件，使用TF*PDF算法查询关键词，以判断该组特定词汇是否满足成为关键词的条件。而由于上述的不足，传统的TF*PDF算法无法快速、高效地对关键词进行查询，以满足用户在线查询的需求。

为此，本文对如何有效地使用TF*PDF算法对关键词进行快速提取进行研究。关键词在线提取的两个核心研究问题是：① 区分不同类别的新闻，以面向不同偏好的用户；② 在用户不断调整查询新闻的类别、时间区间的条件下，快速、高效地对关键词进行提取。因此，设计在类别、时间两个维度上对关键词进行在线查询的方法依然是一个具有挑战性的问题。针对上述传统方法的缺点，本文将TF*PDF算法与Prefix Cube结合，优化TF*PDF算法的词频统计、包含关键词的文档数统计的过程，提出一种高效地对二维新闻数据进行关键词提取并查询最大时间范围的方法(PCTF)，以根据用户提供的词汇，快速寻找这些词汇能够成为热点词汇的最大区域。

1 相关研究

本文所使用的主要符号如表1所示。

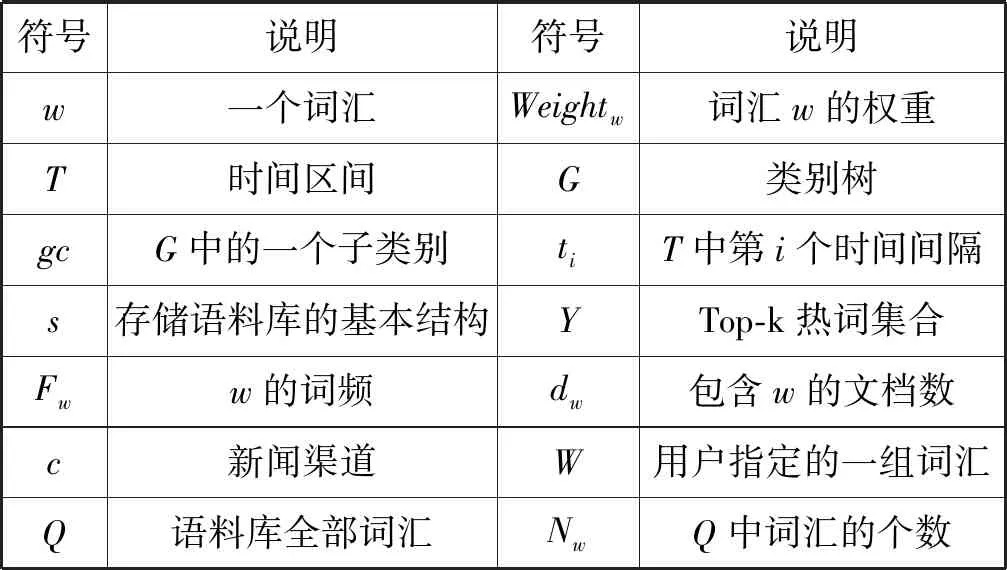
表1 符号说明

1.1 话题检测与追踪

话题检测与追踪(TDT)的研究始于1996年[10]，旨在从大量的新闻数据流中发现并追踪新兴事件和话题。一个话题由一个种子事件或活动以及与其直接相关的事件或活动组成[11]。热门话题是指在一段时间内，在某个领域受到人们广泛关注和讨论的话题，同时该话题被多个媒体广泛报道。热点话题检测与追踪是指发现在一定时期内的热门话题，并在此基础上判断后续新闻报道与该话题的相关性，从而实现追踪功能。

国内外学者在TDT的基础上提出了许多热门话题检测和追踪的方法，其中一种流行的方法是基于词汇权重，检测文章内容中关键或具有代表性的词汇。常用的方法有Salton等提出的TF-IDF算法[6]，另一个是Bun等提出的TF*PDF算法[7]。与TF-IDF方法相比，TF*PDF算法将更多的权重赋予在整个语料库中出现频率较高的词汇，因此，TF*PDF算法提取的关键词能够更好地反映话题的热度，更适用于整个语料库上的热点词汇提取。

1.2 TF*PDF算法

在传统的TF*PDF算法中，某个词汇在单个新闻渠道的权重与其在该渠道的词频成线性正相关，且与该渠道中包含该词汇的文档数成指数正相关。单词在所有渠道中的权重为其在单个渠道中权重之和，其计算过程如下所示：

(1)

(3)

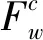
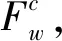
TF*PDF通过计算词汇的词频以及包含该词汇的文档数，来寻找大多数渠道中能够代表热点话题的关键词。当用户改变查询的时间或类别区间时，TF*PDF算法需要遍历区间内的文档，来计算词汇在该区间内的词频和包含该词汇的文档数，导致了大量的重复计算，使得传统的TF*PDF算法无法满足用户频繁改变查询条件的需要。

2 问题定义

本文研究的主要问题为如何根据用户给定的一组词汇，快速寻找这组词汇能够成为热点词汇所处的最长时间区间。

定义1(时间区间T(a,b)) 语料库的一个时间区间T(a,b)={ta,ta+1,…，tb}，其中ti表示语料库的第i个时间间隔，也即语料库中最小的时间单位。特殊地，T(1,Nt)表示语料库中的整个时间区间，其中Nt表示语料库中包含的全部时间间隔。

定义2(类别树G) 语料库中的新闻具有类别属性，所有的类别构成了一个树状结构G。G中的一个子类别gci={gcx,gcx+1,…,gcy}，其中gcj表示类别gci的第j个子类别。

定义3(类别区间G(x,y)) 类别树G的所有叶子节点被定义为{g1,g2,…,gNg}，则一个类别区间G(x,y)={gx,gx+1,…,gy}。特殊地，G中的每一个子类别gc都构成一个类别区间。

定义4(词汇列表L) 语料库中的一个词汇列表Lmn={Lwmn}={(w,Fwmn,dwmn)|w同时出现在gm和tn}，其中w是一个词汇，Fwmn是w在gm和tn中所有文档的词频，dwmn是在gm和tn中包含w的文档数。

定义5(基本数据结构s) 用于存储一个语料库的一个基本数据结构s={Lmn|1≤m≤Ng,1≤n≤Nt}。

定义6(Top-k热词Y) 所有语料库在某个时间区间T(a,b)和一个子类别gc的Top-k热词为一个词汇集合Y={w1,w2,…,wk}，且对于该区间的词汇w∈Y,w′∉Y，有Weightw≥Weightw′。

基于以上的定义，本文研究的主要问题的形式化定义如下：

定义7(热词最长时间区间查询)

给定一组词汇W={w1,w2,…,wl}，G中的一个子类别gc，查询初始时间间隔ta，正整数k，寻找一个最长的时间区间T(a,b)，对∀w∈W,∀i∈(a,b)，在T(a,i)中，有w∈Y。

3 基于改进TF*PDF的热词最长区间查询方法

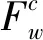
3.1 PC:Prefix Cube

文献[12]使用Prefix Sum技术提出了一个名为Prefix Cube(PC)的存储结构。给定存储一个语料库的基本数据结构s，首先计算其中一个词汇w词频Fw的Prefix Cube表示为:

(4)

对于一个时间区间T(a,b)和一个子类别gc=G(x,y)，w在这个区间内的词频Fw可以通过FPC快速计算：

FPCw(y,b)-FPCw(y,a-1)-

FPCw(x-1,b)+FPCw(x-1,b-1)

(5)

式(5)表明，Fw在区间T(a,b)和子类别gc=G(x,y)构成的二维区间内的词频可以通过该二维区间顶点的FPCw来快速计算，从而避免了对该二维区间内的全部文档进行迭代计算。

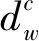
DPCw和FPCw同样具有式(5)所示的性质，在区间T(a,b)和子类别gc=G(x,y)构成的二维区间，有:

DPCw(x-1,b)+DPCw(x-1,b-1)

(7)

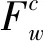
当x=y=m，a=b=n时，式(5)和式(7)可变化为：

Fw=FPCw(m,n)-FPCw(m,n-1)-

FPCw(m-1,n)+FPCw(m-1,n-1)=Fwmn

(8)

dw=DPCw(m,n)-DPCw(m,n-1)-

DPCw(m-1,n)+DPCw(m-1,n-1)=dwmn

(9)

因此，可以通过迭代的方式来计算FPCw和DPCw：

FPCw(m,n)=FPCw(m,n-1)+FPCw(m-1,n)-

FPCw(m-1,n-1)+Fwmn

(10)

DPCw(m,n)=DPCw(m,n-1)+DPCw(m-1,n)-

DPCw(m-1,n-1)+dwmn

(11)

式中：FPCw(1,1)=Fw11,DPCw(1,1)=dw11。因此FPCw和DPCw可以通过迭代的方式进行构建，而不需使用式(4)和式(6)对已经计算出的所有元素进行循环计算。接下来，将FPCw和DPCw合并，以构建出w的Prefix Cube：PCw。最后对所有的单词进行迭代计算，以构建出整个语料库存储s的Prefix Cube：PC。

对PC的构建算法的详细描述如算法1所示。

算法1构建PC

ConstructPC(s,Nt,Ng,Q)

输入：语料库的基本存储结构s，时间间隔个数Nt，类别树的所有叶子节点个数Ng，全部词汇Q

输出：所有单词的Prefix Cube：PC

1:Forw∈QBegin

2: FetchFw11,dw11froms;

3: FPCw(1,1)=Fw11,DPCw(1,1)=dw11;

4:Form∈(1,Ng)Begin

5:Forn∈(1,Nt)Begin

6:FetchFwmn,dwmnfroms;

7:FPCw(m,n)=FPCw(m,n-1)+FPCw(m-1,n)-

FPCw(m-1,n-1)+Fwmn;

8:DPCw(m,n)=DPCw(m,n-1)+DPCw(m-1,n)-

DPCw(m-1,n-1)+dwmn;

9:PCw(m,n)=(w,FPCw(m,n-1),DPCw(m,n-1));

10:End

11:End

12:End

13:PC={PCw};

14:ReturnPC;

在算法1中，构建PC需要对语料库中的全部词汇、时间间隔和类别树的叶子节点做循环，因此，算法的时间复杂度为O(NwNgNt)。对于构建出的PC，由于每个PCw的每个元素需要存储w、FPCw(m,n)和DPCw(m,n)，每个PCw的空间复杂度为O(3NtNg)。因此，整个PC的空间复杂度为O(3NwNtNg)，和原始的s的空间复杂度相同。因此使用PC作为语料库辅助存储并不增加存储的空间复杂度。

3.2 最长时间区间查询

根据第2节的问题定义，本文所涉及的查询为用户给定一组单词、初始时间间隔、类别和k，查询该组单词在该类别上满足成为热词的最长时间区间。这就要求算法不断地更新时间区间，计算出词汇的权重，以判断词汇是否是Top-k的热词。

当使用传统的TF*PDF算法时，时间区间需要不断地被更新来计算词汇权重以查找Top-k的热词，TF*PDF算法中的词频和包含词汇的文档数需要进行大量的重复计算。而当使用PC作为存储结构时，由于词频和文章数可以通过式(5)和式(7)直接得出，这些计算可以被避免。

当用户给定一组词汇W={w1,w2,…,wl}、初始时间间隔ta、类别gc和k，查询该组单词在该类别上满足成为热词的最长时间区间时，我们以ta为初始点，对ta后的时间间隔进行遍历以查询热词，并判断W是否在Top-k热词Y中，如算法2所示。

算法2PCTF：查询最长时间区间

PCTF(W,ta,gc,k,PC,Q)

输入：词汇W={w1,w2,…,wl}，初始时间间隔ta，类别gc，整数k，所有语料库的Prefix CubePC={PC1,PC2,…,PCNc}，全部词汇Q

输出：时间区间T(a,b)

1:b=a;

2:{gx,gx+1,…,gy}=gc;

3:Do

4:Weight=∅;

5:D=∅;

6:b=b+1;

7:Forc∈(1,Nc)Begin

9:lc=0;

Forw∈QBegin

12:End

13:End

14:Forw∈QBegin

15:Weightw=0;

16:Forc∈(1,Nc)Begin

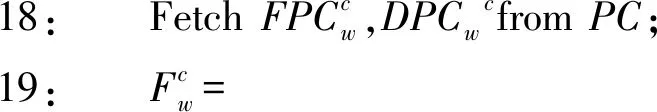
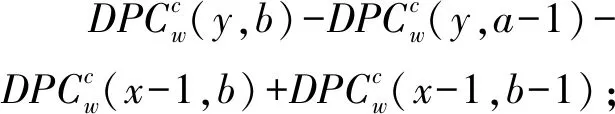
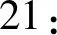
22:End

23:Weight=Weight∪Weightw;

24:End

25:Y=Top-k(Weight);

26:WhileW⊂Y;

27:ReturnT(a,b-1);

算法2首先获取给定类别gc的类别区间(x,y)，在7～13行，该算法计算在每个Channel中的词频的平方和，时间复杂度为O(NcNw)。随后算法2依次迭代更新时间区间的终止时间间隔tb，并使用Prefix Cube查询T(a,b)上所有单词的权重，时间复杂度同样为O(NcNw)。最后算法计算Top-k的热词，直到用户给定的词汇W不满足热词的条件，算法返回时间区间T(a,b-1)。在计算Top-k热词时，使用最小堆技术，时间复杂度为O(Nwklogk)，而判断W⊂Y需要O(k)的时复杂度，因此，算法的总复杂度为(b-a)O(Nwklogk+2NcNw)。

4 实 验

本节设计了一系列实验来比较PCTF算法和传统的TF*PDF算法在提取热词并查询热词所在的最长时间区间的运行效率。

4.1 语料库

为测试PCTF算法的效率，本文从一些著名的新闻网站——路透社(https://uk.reuters.com)，纽约时报(https://www.nytimes.com)和BBC(https://www.bbc.com)上收集了自2016年1月1日至2017年1月1日的新闻文章。表2列出了三个语料库的详细信息。

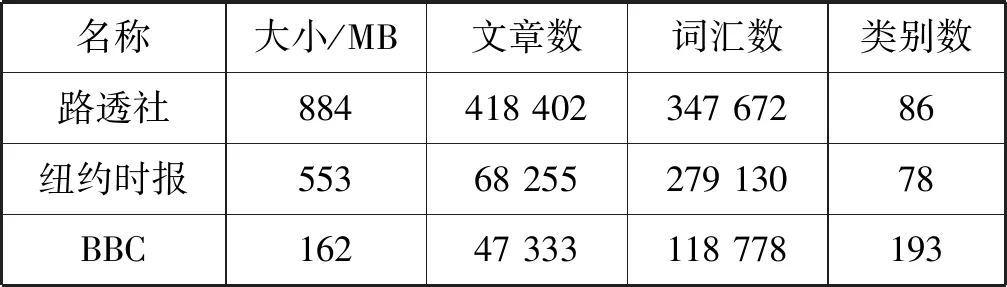
表2 语料库详细信息

实验中，渠道总数Nc=3，语料库的最小时间单位为天。本文使用了Stanford CoreNLP对语料库进行了预处理，包括去除停止词、分词和词形还原等。

4.2 实验环境

采用的实验环境为：Intel®Xeon(R) CPU E5-2650v3 @ 2.30 GHz×40，128 GB内存和256 GB SSD磁盘，操作系统为Ubuntu Kylin 16.04，程序语言为Java (Version 1.8.0_92)。

4.3 寻找最长时间区间

(1) 改变k通过改变k，研究不同的k对PCTF算法查询热词所满足的最长时间区间的时间开销的影响。在本次实验中，设置初试时间间隔为2016年6月15日(ta=288)，类别为politics(gc=politics，类别区间长度为23)，用户给定的一组词汇W={Trump,Clinton,Obama,President}。实验结果如图1所示。

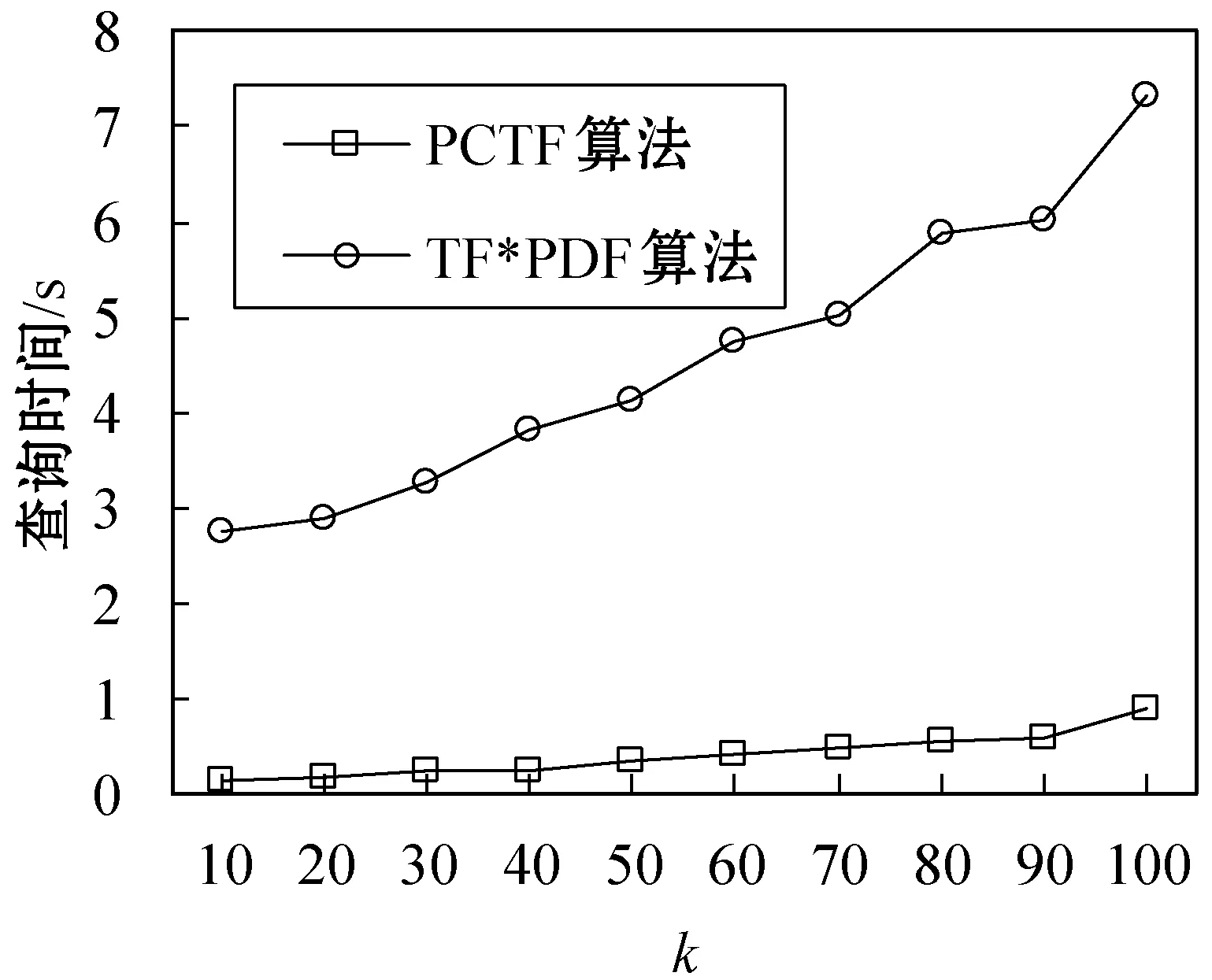
图1 改变k时查询时间的变化曲线

从图 1可以看出，随着k的增加，PCTF算法和传统的TF*PDF算法查询最大时间区间所消耗的时间均有所增加，这是因为在计算出所有词汇的权重之后，算法需要计算Top-k的热词。此外，随着k的增加，用户给定词汇满足Top-k的最长时间区间的范围也可能增加。因此，两个算法的整体时间消耗均有所增加。然而，随着k的增加，PCTF算法的时间开销均远小于TF*PDF算法。

(2) 改变类别和用户指定的词汇 通过改变类别和用户指定的关键词，研究PCTF算法对于不同用户偏好的适用性。实验设置初始时间间隔为2016年8月1日(ta=213)，k=50，类别和词汇分别为：

①gc=basketball，类别区间长度为5，W={NBA,Rockets,Harden}；

②gc=football，类别区间长度为8，W={Spain,Argentina,Ronaldo,Messi}；

③gc=tennis，类别区间长度为3，W={Nadal,Federer,Final}。

实验结果如图2所示。

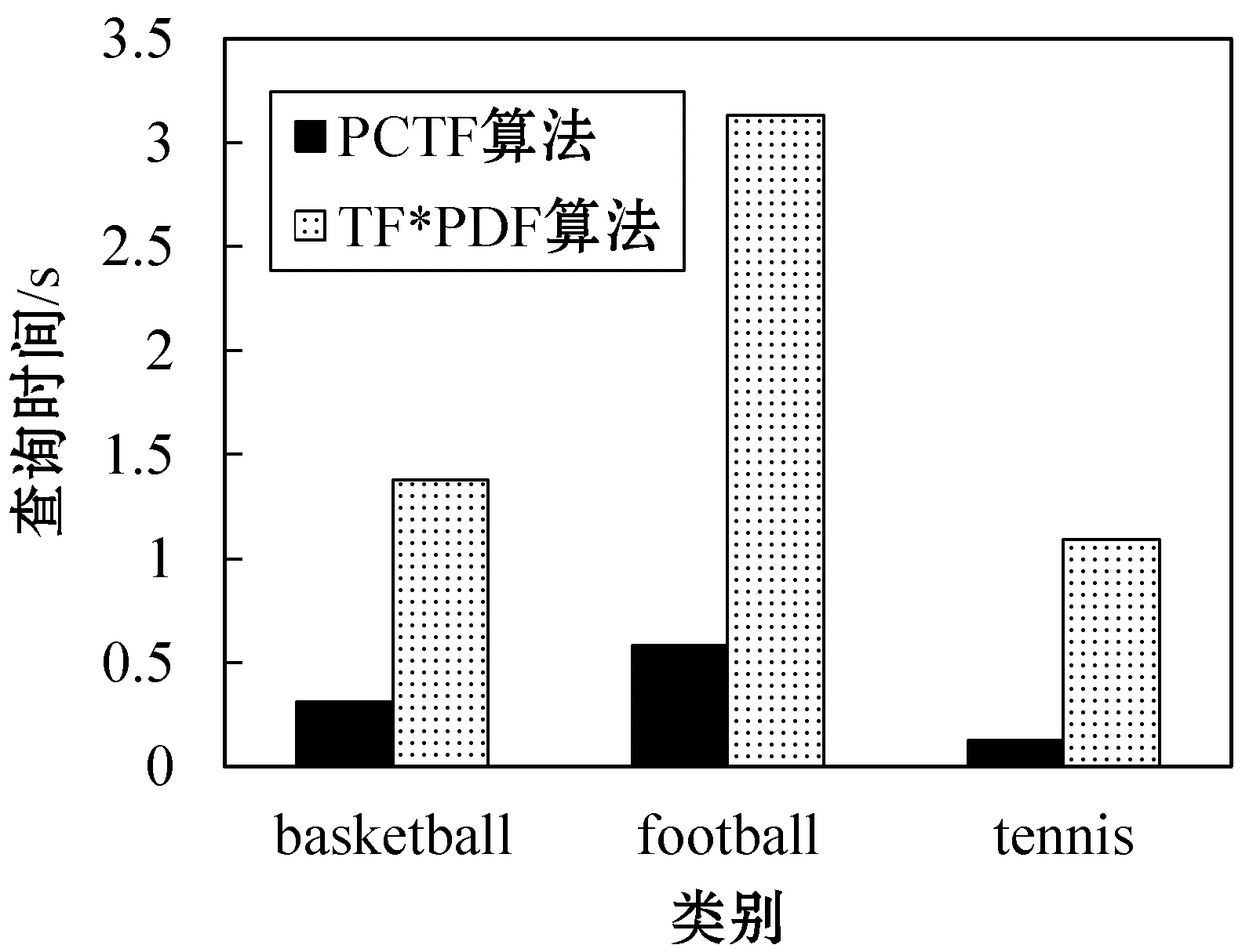
图2 改变类别和关键词时查询时间变化的柱状图

由图 2可以看出，对于不同的类别和用户指定的词汇，两种算法在较大的类别区间上有较高的查询时间。而与TF*PDF算法相比，PCTF算法均能以较低的查询时间得到最大的时间区间。

(3) 改变初始时间间隔 由于一组词汇可以在不同的时间区间内都成为热词，也即该组词汇描述的事件发生了多次，可以通过改变初始时间间隔来更加全面地寻找词汇能够成为热词的最长时间区间。

实验设置类别为Sports(gc=Sports，类别区间长度为14)，W={NBA,Rockets,Lakers}，k=50，初始时间间隔分别为2016年1月18日(ta=17)，2016年4月11日(ta=101)，2016年10月27日(ta=300)，2016年12月8日(ta=342)。实验结果如图3所示。

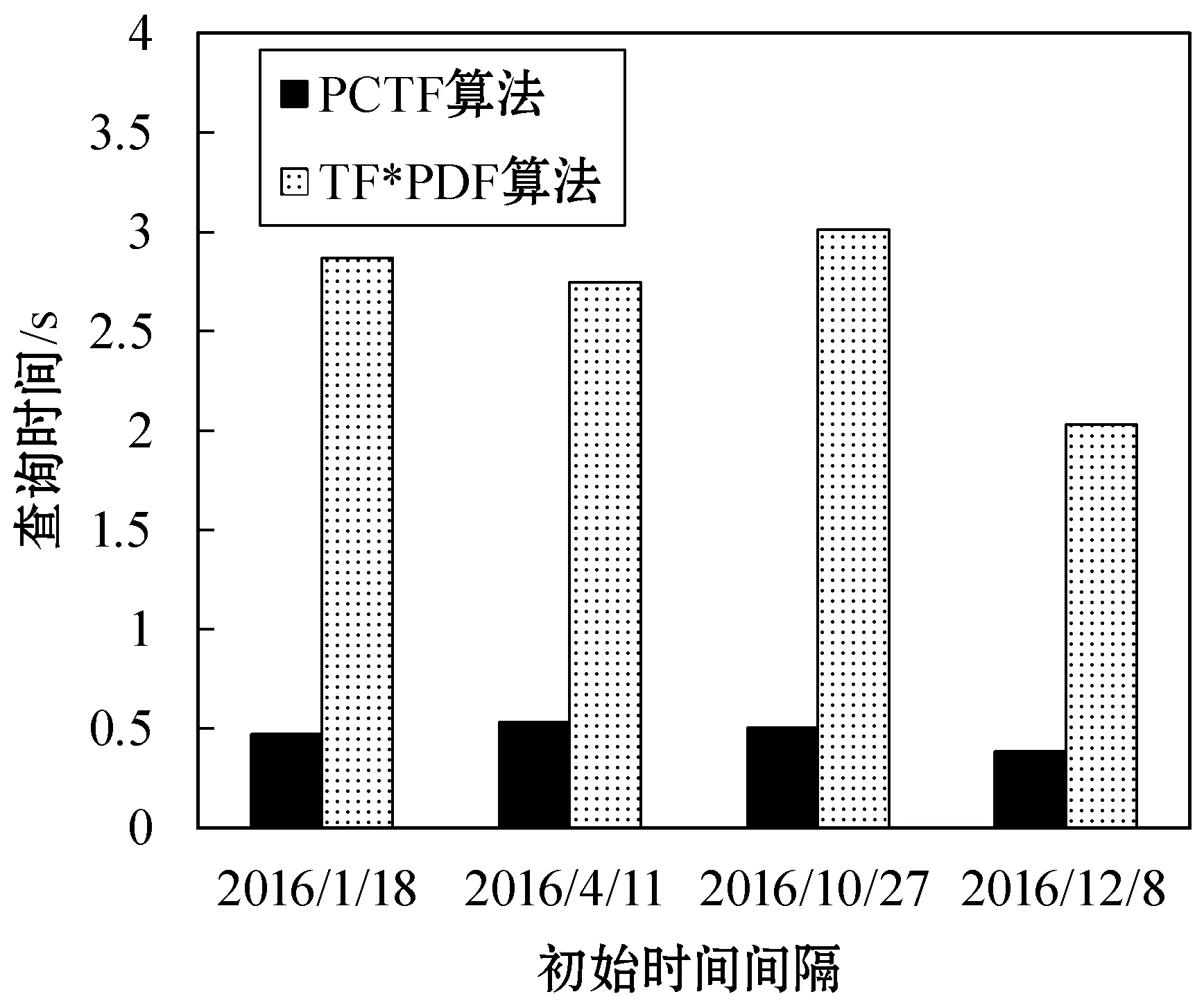
图3 改变初始时间间隔时查询时间变化的柱状图

由图3可以看出，当改变查询的初始时间间隔时，PCTF算法均能保持较低的查询时间复杂度，且查询时间较为稳定。

通过以上的实验我们可以看出，PCTF算法能够较好地应对不同的查询场景。当用户不断改变k、查询类别和词汇以及查询的初始时间间隔时，传统的TF*PDF算法耗时较长，而PCTF算法均能以小于1 s的时间消耗查询出用户给定词汇的最长时间区间。因此PCTF算法能够面向不同的用户，快速高效地对关键词进行提取，并查询词汇所在的最长时间区间。

5 结 语

本文对二维区间内关键词提取的在线算法进行研究。基于Prefix Cube，对传统的TF*PDF算法进行改进，提出了FPC、DPC的存储结构，快速、高效地对关键词进行提取，并能快速查询用户指定的词汇成为关键词的最长时间区间。PCTF算法在空间复杂度不变的情况下，降低了关键词提取的时间复杂度，具有能够面向不同偏好的用户和较好地应对用户不断更新查询条件的优点。试验结果表明，PCTF算法在不同查询条件下，查询所用时间优于传统的TF*PDF算法。在自然语言处理方面，由于本文的算法采用Stanford CoreNLP对新闻文章进行分词，算法对中文文档的支持性不足。在未来的研究中，将考虑数据的更新及更加复杂的查询，此外，将考虑使用更多中文分词库以增加算法对中文文档的支持能力。