基于同态滤波和维纳滤波的太阳耀斑去云处理对比研究
2019-08-13胡品端黎子晋袁国淳
胡品端 黎子晋 袁国淳

摘 要:对于太阳耀斑图像去云处理的研究,该文建立了基于同态滤波的去云模型以及基于维纳滤波的去云模型。通过两种模型分别处理图片,对比分析结果图后得出两种模型对太阳耀斑去云处理均有一定效果。但基于同态滤波的去云模型更适于太阳耀斑图片的去云处理,同时通过三维图像可以得出同态滤波去云效果最佳。
关键词:同态滤波 维纳滤波 去云处理 三维图像处理
中图分类号:TP751 文献标识码:A 文章编号:1672-3791(2019)05(b)-0015-03
太阳耀斑是一种发生于太阳大气周围局部的一种最剧烈的太阳的爆发活动现象。其在短时间内释放出大量能量并引起局部区域瞬时急剧加热,并向外发射各种电磁辐射。近年来,对太阳耀斑的研究受到越来越多研究人员的青睐,但是在观测时几乎都会受到云的遮挡,所拍摄到的太阳耀斑图片需要经过一定的处理才能对其进行研究。因此,建立合理的模型对太阳耀斑图片进行处理,在当下具有一定的现实意义和参考价值。
同态滤波一种广泛用于图像处理的技术,其实质上是高通滤波和图片亮度的非线性变换的结合,由于云雾处于低频,而运用同态滤波可减少低频增加高频,从而实现减少光照变化并锐化细节,可获得清晰的太阳耀斑无云图。但由于同态滤波作为一种全局性的变化,其具有一定的局限性。因此在同态滤波分析法的基础上,选用维纳滤波法对图像再次进行去云处理。该文基于上述两种方法分别对太阳耀斑图片进行去云处理,对结果进行对比,得出更为理想的太阳耀斑去云处理方法。
1 基于同态滤波的太阳耀斑去云处理模型
考虑到是否有云遮挡所接受的光占据不同的频带,通过傅里叶变换可将图像变换到频率域,设计一个高通滤波器,以去除低频分量(云的影响),同时考虑到滤掉低频分量后应以物体原色光补充,采用同态滤波法,即把频率过滤和灰度变换结合起来的一种处理方法。根据云覆盖信息在频率域上通常占据低频信息这一特点,将云层除去,同时增强云覆盖下的背景信息。
2.5 读取数据得到去云图片
根据傅立叶反变换得到的灰度系数矩阵重新构建去云图片,即可得到太阳耀斑去云处理后的图片。
3 基于同态滤波与维纳滤波的太阳耀斑去云处理结果分析
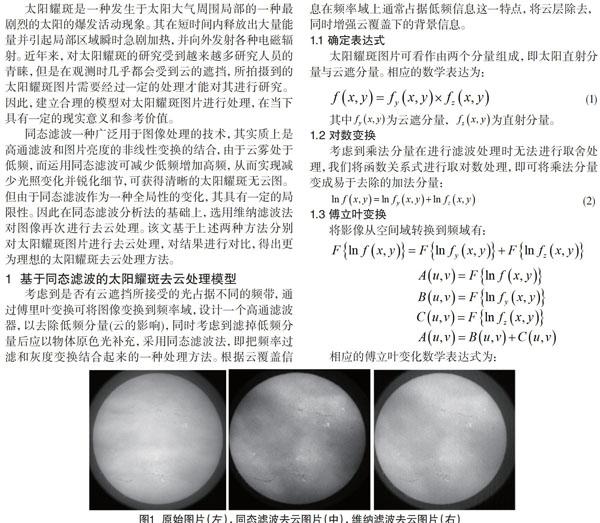
对上述两种模型运用MATLAB进行求解所得到的去云图像与原图对比如图1所示。
根据图像对比可知,去云后的图像与原图相比显得更有层次感,省去了原图被云雾遮挡的模糊感。其中白色光点部分即为太阳耀斑部分,被云遮挡的耀斑也显现出来,在原图中可以看到的耀斑顯得更加清晰可见,灰度不同而导致的图形内对比也更加明显。由此可见,运用同态滤波与维纳滤波法求得得到的去除云雾遮盖后的图像均达到了理想观测太阳耀斑的效果。
4 最优结果分析
为得到最优的去云处理图像,特对两种模型进行对比分析,以得到最优结果。
为了获得更加直观的视觉对比感受,我们基于灰度以及像素(横纵)三因素将其转换为三维图形,如图2所示。
根据上述三维对比图可以十分直观地看到,三维图形中凸出的刺状部分即为太阳耀斑。图2左图整体呈现出高低状态平稳,颜色融合较深的状态,但经过去云处理后的右图太阳耀斑与太阳整体的区分显得十分明显。不难看出,太阳耀斑的灰度远高于普通阳光,因此在三维图中十分突出。而维纳滤波模型处理后的图形虽然能够看到太阳耀斑,但是去除得不够准确,更偏向于全局处理,效果不及同态滤波模型。同态滤波模型经过同态滤波模型处理后的去云图片能够更加清晰地观测到太阳耀斑的位置,与周围的对比更加明显。因此在对比分析之下,虽然两种模型均有一定效果,但同态滤波模型的去云效果较维纳滤波模型更好。
从上述对比分析中,我们都能直观地看到经过去云处理后的图像更加清晰,去除云雾干扰后太阳耀斑显示得十分明显。由此证明了该模型的正确性与实用性,且说明该模型在对太阳耀斑图像观测时具有一定的实际参考及推广意义。
5 结语
通过上述两种算法的结果分析对比以及最优结果分析可知:(1)基于同态滤波和维纳滤波的去云处理均对太阳耀斑图片的更清晰准确展示有一定的作用;(2)同态滤波模型处理后的太阳耀斑突出得更加明显,而维纳滤波模型处更偏向于全局处理,因此对于太阳耀斑图片的去云处理更适合采用基于同态滤波的模型。
参考文献
[1] 赵孟银.遥感影像去云方法研究[D].天津科技大学,2016.
[2] 秦川,李小飞.基于频域直方图和HVS的彩色图像质量评价算法[J].电视技术,2015,39(15):28-33.
[3] 向方明,朱遵义,许敬,等.YUV到RGB颜色空间转换算法研究[J].现代电子技术,2012,35(22):65-68.
[4] 周姗姗,柴金广.图像预处理的滤波算法研究[J].科学技术与工程,2009,9(13):3830-3832,3839.
[5] 杨文涛.傅里叶变换在数字图像处理中的应用研究[D].华中科技大学,2007.
