RBF神经网络可靠度分析方法在边坡稳定性研究中的应用*

何永波，李 青，张 宁，李闯将

(中国计量大学 灾害监测技术与仪器国家地方联合工程实验室，浙江 杭州 310018)

0 引言

边坡稳定性分析是对滑坡灾害预警和治理的关键方法之一，目前边坡稳定性的分析方法主要分为2大类：确定性分析法和不确定分析法。确定性分析法目前应用较广泛的是以极限平衡理论为基础的安全系数法，但由于实际边坡存在大量的不确定性，包括计算参数的变异性和随机性[1]，该方法很难反映出边坡的实际工作状态；不确定分析中，最具代表性的是基于概率分析的可靠度分析方法，该理论把各不确定因素看作随机变量来分析边坡破坏的可能性，根据已知的随机变量统计参数和概率分布模型以及给定的功能函数估计边坡在规定时间和条件下完成预定功能的概率[2],将不能完成功能的概率称之为失效概率[3]。

可靠度理论是建立在土体具有的抗力大于荷载效应的概率基础上进行设计和校核的，因此分析结果更符合客观实际。边坡可靠度的计算常用方法有一次二阶矩法(中心点法、设计验算点法)、蒙特卡罗模拟法、响应面法等。一次二阶矩法计算的精度较低，蒙特卡罗法简单且计算精度高，但是计算量偏大[4]。近年来，随着非线性理论的发展，基于替代模型的可靠度分析开始应用起来，利用替代模型来近似构造函数，将复杂的边坡稳定隐式功能函数显示化[5]，降低工作量，提升工作效率。常见的替代模型有利用响应面对边坡可靠度研究，神经网络、支持向量机[6]等智能算法，给边坡的稳定性分析开辟了新的途径。针对之前各研究方法所遇到的问题，本文提出一种基于粒子群算法(PSO)优化径向基函数(RBF)神经网络的边坡可靠度分析方法。

1 分析方案

本文主要根据地质勘探和室内外的土工试验得到边坡岩土体物理参数(黏聚力c值和内摩擦角φ值)；利用强度折减法计算c,φ对应的安全系数；将各组数据作为模型的训练样本带入RBF网络模型进行训练，利用模型强大的数据拟合能力，映射出安全系数和c，φ之间的关系，并使用PSO算法进一步优化，构建响应面功能函数；结合蒙特卡罗法(Monte Carlo)产生大量的随机数样本模拟求解边坡失稳概率，分析方案见图1。

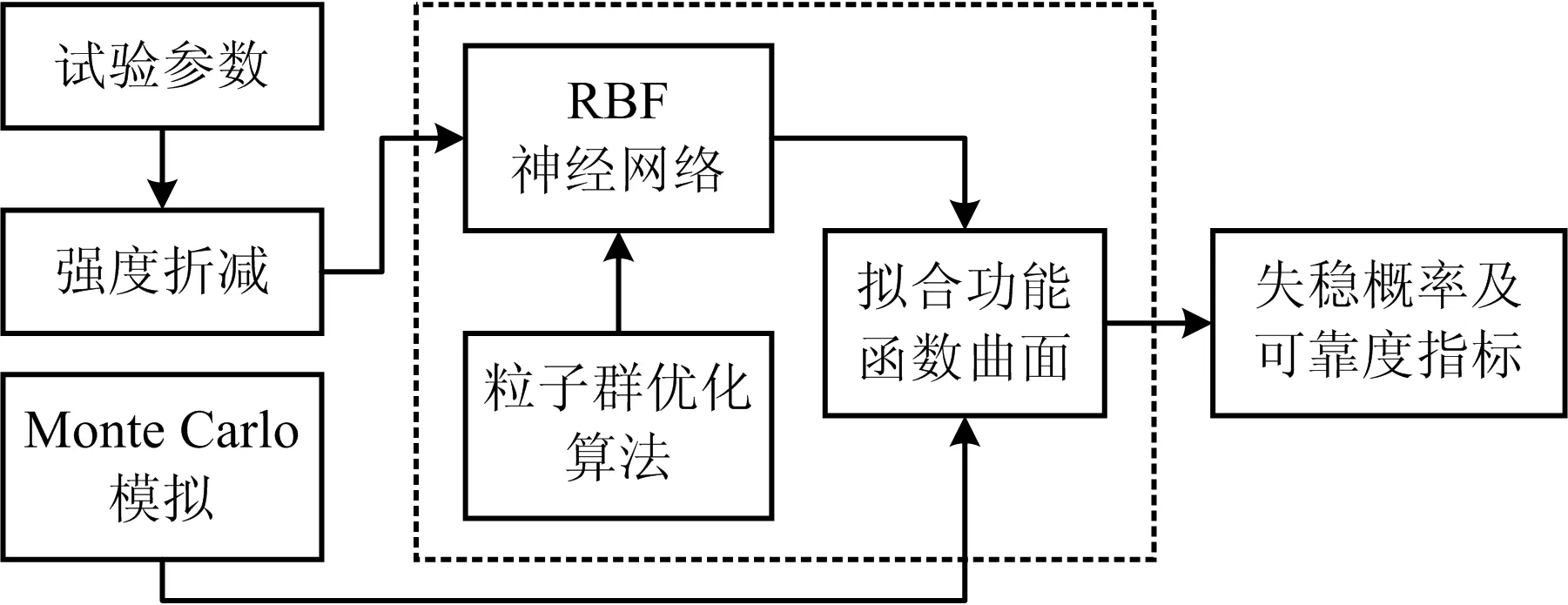
图1 分析方案设计Fig.1 Design of analysis scheme

2 基于RBF网络的可靠度分析

2.1 ABAQUS强度折减法

强度折减法最早由Zienkiewicz等提出，后被许多学者广泛采用并提出了抗剪强度折减系数(SSRF)的概念[7]，定义为：假设外载荷保持不变，边坡内土体所能提供的最大抗剪强度与外载荷在边坡内所产生的实际剪应力之比。当边坡内所有土体抗剪强度的发挥程度相同时，这种抗剪强度系数相当于稳定安全系数FS。

折减后的抗剪强度参数可分别表达为:

cm=c/Fr

(1)

φm=arctan(tanφ/Fr)

(2)

式中：c和φ是土体所能提供的抗剪强度参数；cm和φm是维持平衡所需的抗剪强度参数；Fr是强度折减系数。

使用强度减法所选取的屈服准则[8]是Mohr-Coulomb：

(3)

式中：c和φ是土体黏聚力和内摩擦角；I1为应力张量的第一不变量；J2是应力偏张量的第二不变量；θ是应力洛德角。因ABAQUS具有求解非线性，处理非均质问题以及模拟各种复杂的材料的优点，故本文选用此方法进行模拟计算。

2.2 RBF神经网络

RBF神经网络是于1989年由Mooden及Darken提出，是由输入层、隐含层和输出层构成的三层前馈式神经网络(见图2)，在参数选择适当的前提下，其能够以给定的精度逼近任意的连续函数[9]。图中R为网络输入数；P为输入向量；S为神经元数；a和IW为该层输出和权值矩阵；radbas为径向基函数；b为隐含层阈值。隐含层常采用K-means算法进行训练，输出层采用递归最小二乘法进行训练。它用径向基函数作为激励函数，由于最常用的基函数为高斯函数，定义第i个隐含单元的激活函数为:

(4)

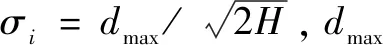
隐含层到输出层映射为：

(5)

其中，可通过最小二乘法获得权重系数ω，向量可表示为ω=[ω1,ω2,…,ωH]，一般通过最小化误差指标函数训练网络,选取均方误差函数为:

(6)

式中：N代表训练样本点的个数；ei代表第i个节点的输出误差,可以表示为:

(7)

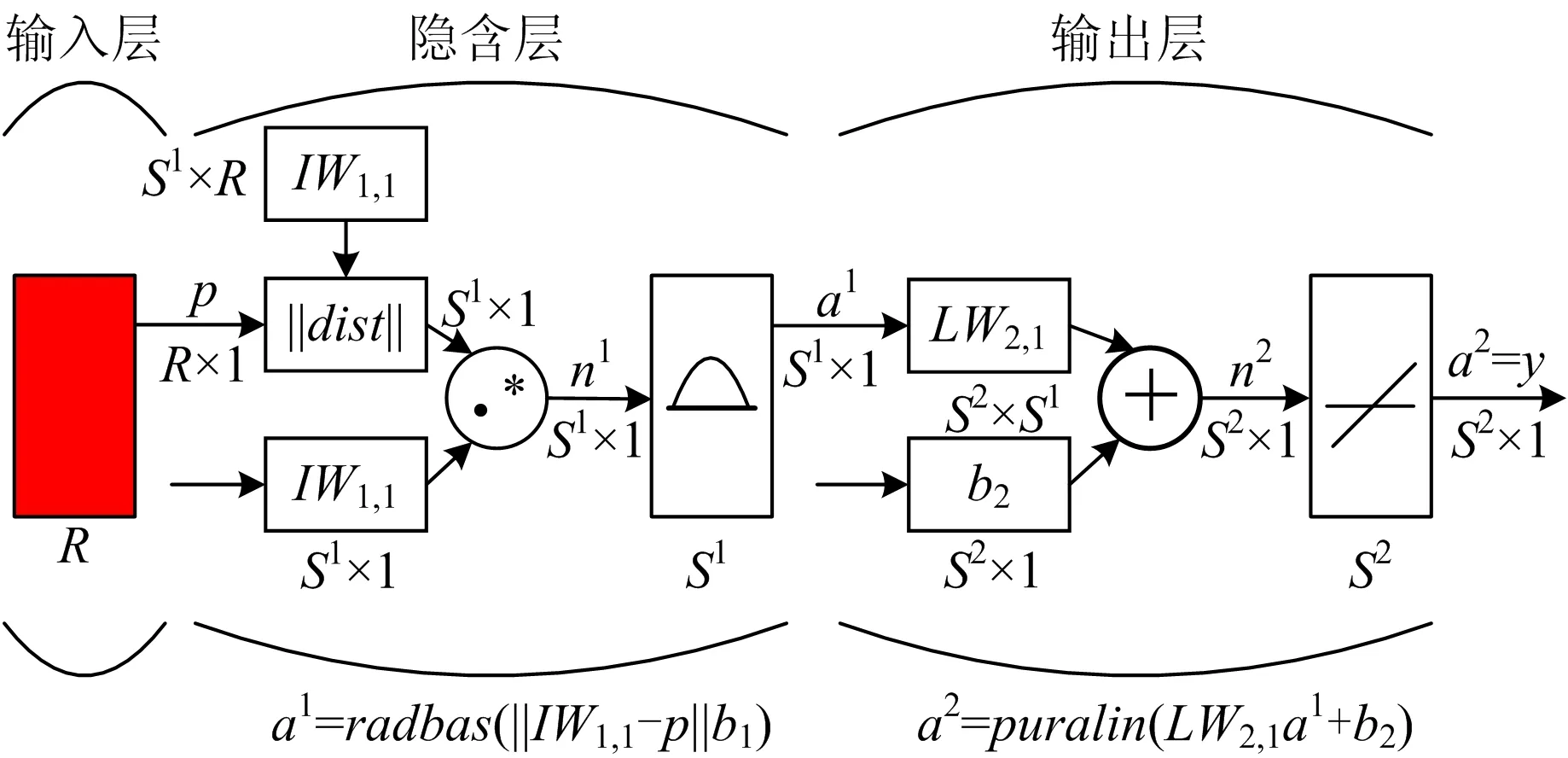
图2 RBF径向基函数神经网络结构Fig.2 Structure of RBF neural network

2.3 PSO算法

PSO算法[10]是基于群体行为的搜索算法，群体中每个粒子在迭代的过程中不断改变本身的速度矢量v和位移矢量x，寻找到全局最佳的位置，粒子的迭代过程满足：

(8)

(9)

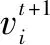
ωt=ω2-t(ω2-ω1)/T

(10)

式中：ω1和ω2分别表示初始和最终迭代权重；t为当前迭代次数；T为最大迭代次数。

PSO优化RBF模型[11]步骤主要包括：

1)模型初始化，种群的规模、迭代的次数和权重；

2)计算每个粒子的适应度，如式(11)：

(11)

式中：yi和fi表示实测值和预测值。

3)以种群中适应度最小的粒子作为gbest

初始值，将粒子当前位置作为最优pbest，找出具有最优适应度值的粒子位置作为pbest。

4)比较个体和种群的最优解适应度，更小的作为gbest。

5)更新粒子的速度和位置以及迭代的权重，直到迭代次数满足结束条件，将gbest对应的粒子作为RBF的参数。

2.4 Monte Carlo模拟方法

Monte Carlo模拟方法是进行可靠度计算的重要手段，又称为随机模拟方法或统计试验方法，由于其限制较小，思路简单，得到了较为广泛的应用[12]。可以假设结构的功能函数已知以及基本随机变量的概率分布，当选取样本数量足够大时，事件实际发生的概率可以通过频率近似得到。

按照滑坡的岩土体性质、变形机制及其受力状态，首先确定状态变量x1,x2,…,xn的参数统计值及概率分布，参数分别代表重度，黏聚力，内摩擦角等，根据RBF拟合的响应面函数确定边坡的结构功能函数为：F=g(x1,x2,…xn)，极限状态方程可表示为Z=F-1,如此重复N次，得到N个相对独立的样本值Z1,Z2,…,Zn，若定Z<0为滑坡失效事件，则在N次抽样中出现M次，则由伯努利大数定理可知，失效概率为：

(12)

式(12)为蒙特卡罗法计算出的失效概率，对于得到的N组Z,其均值和标准差分别为：

(13)

(14)

用β表示可靠度指标，则β可表示为：

β=μz/σz

(15)

则失效概率：

Pf=Φ(-β)=1-Φ(β)

(16)

式中：Φ(β)为标准正态分布。

3 实例分析

半岭滑坡位于浙江省丽水市遂昌县黄沙腰镇村下半岭自然村，距离遂昌县城约85 km，半岭滑坡所在地区雨季降雨强度大，山区水流流速大，极易引起滑坡。滑坡平面上总体呈“舌状”，主轴倾向215°，滑坡堆积体平面投影长540 m，前缘宽约220 m，后缘宽约190 m,高程460～670 m，根据钻孔揭露厚度为0～25.9 m，滑坡区域的现场勘察如图3所示。

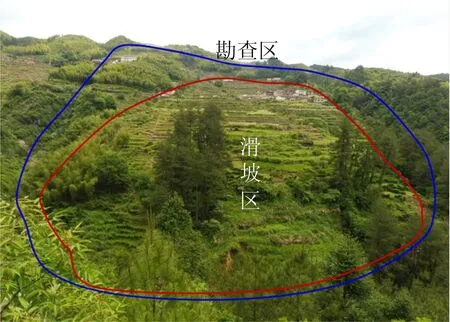
图3 半岭滑坡工程现场Fig.3 Site map of Banling landslide project

根据现场调查发现位于滑坡前缘2处小规模滑坡现象，2018年6月多雨天气，钻孔ZK02附近再次发现长裂缝，该滑坡地下水丰富，软弱土层浸泡软化，工程力学性质降低，导致堆积体发生失衡，沿软弱夹层发生蠕动，工程地质平面图如图4，工程地质剖面图如图5。

根据半岭A区滑坡目前处于临界状态这一现状，结合土工实验以及现场勘察得出最终的计算参数，取多组黏聚力c值和内摩擦角φ值，并计算其均值、标准差、变异系数，见表1。

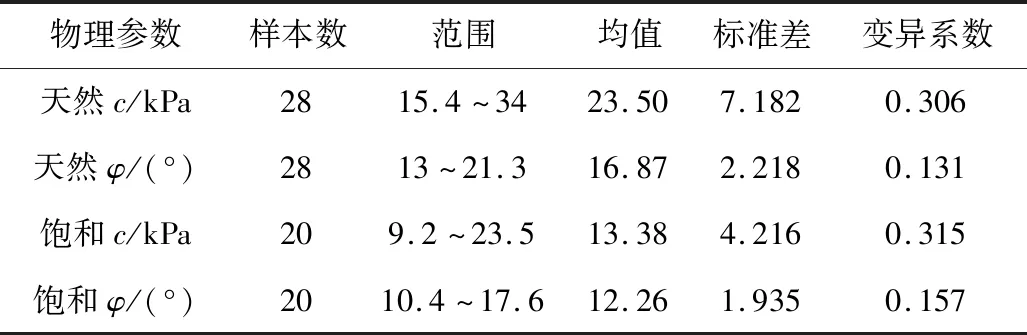
表1 滑带土物理参数Table 1 Physical parameters of soil in slip zone

3.1 求解边坡安全系数

参考Dawson等分析的一个均质土坡[7]建立和实际边坡近似的算例。将饱和状态下参数的均值作为输入：黏聚力c=13.38 kPa，内摩擦角φ=12.26°，重度γ=20 kN/m3，杨氏弹性模量E=20 MPa，变异系数δ=0.315，泊松比ν=0.3。

首先，在ABAQUS软件中建立部件，绘制边坡几何轮廓，设置材料属性以及截面特性；其次，装配部件以及定义分析步之后需要定义载荷以及边界条件、划分网格；最后，修改模型的输入文件，控制场变量变化，进行结果分析。

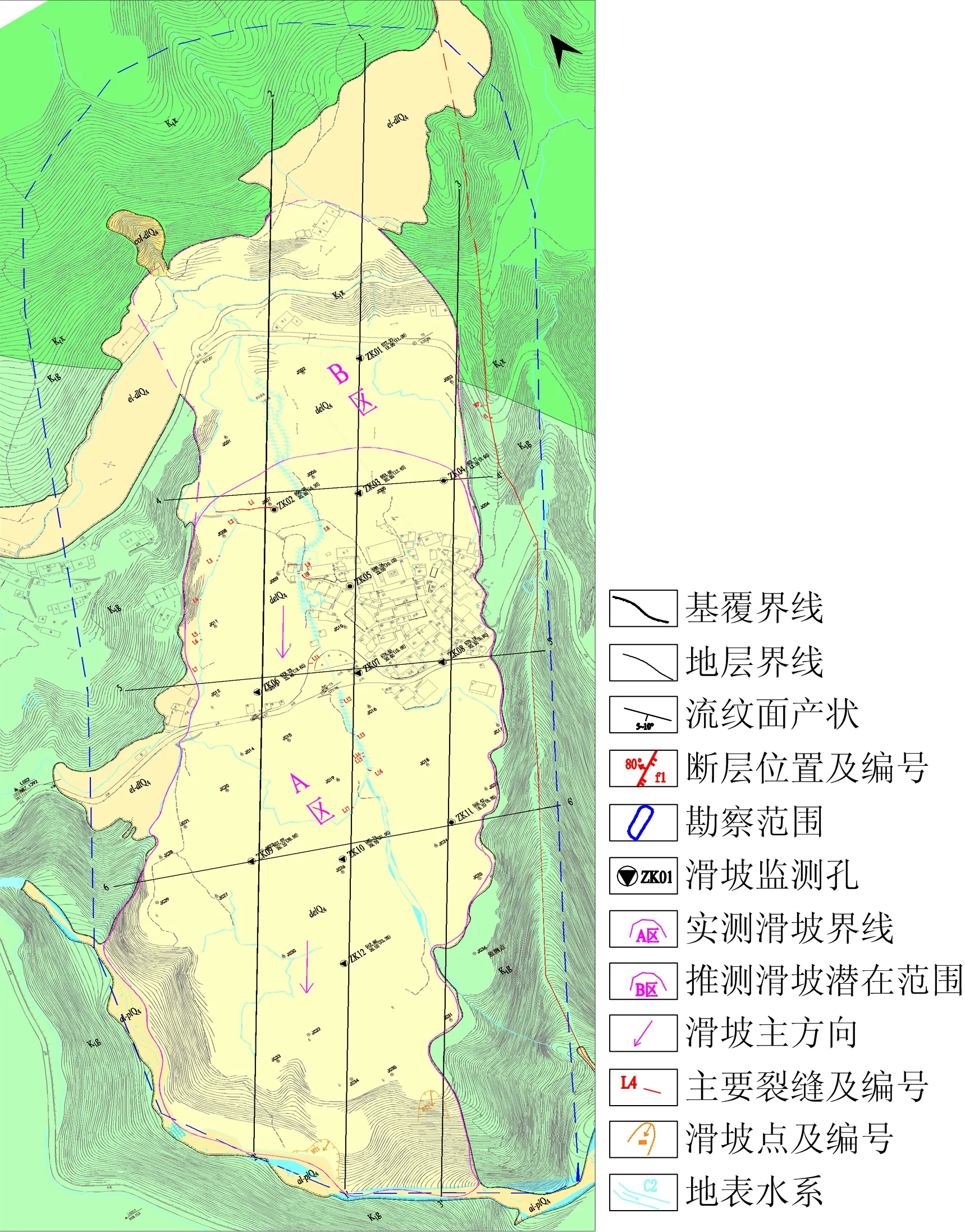
图4 半岭工程地质平面Fig.4 Engineering geological plane of Banling

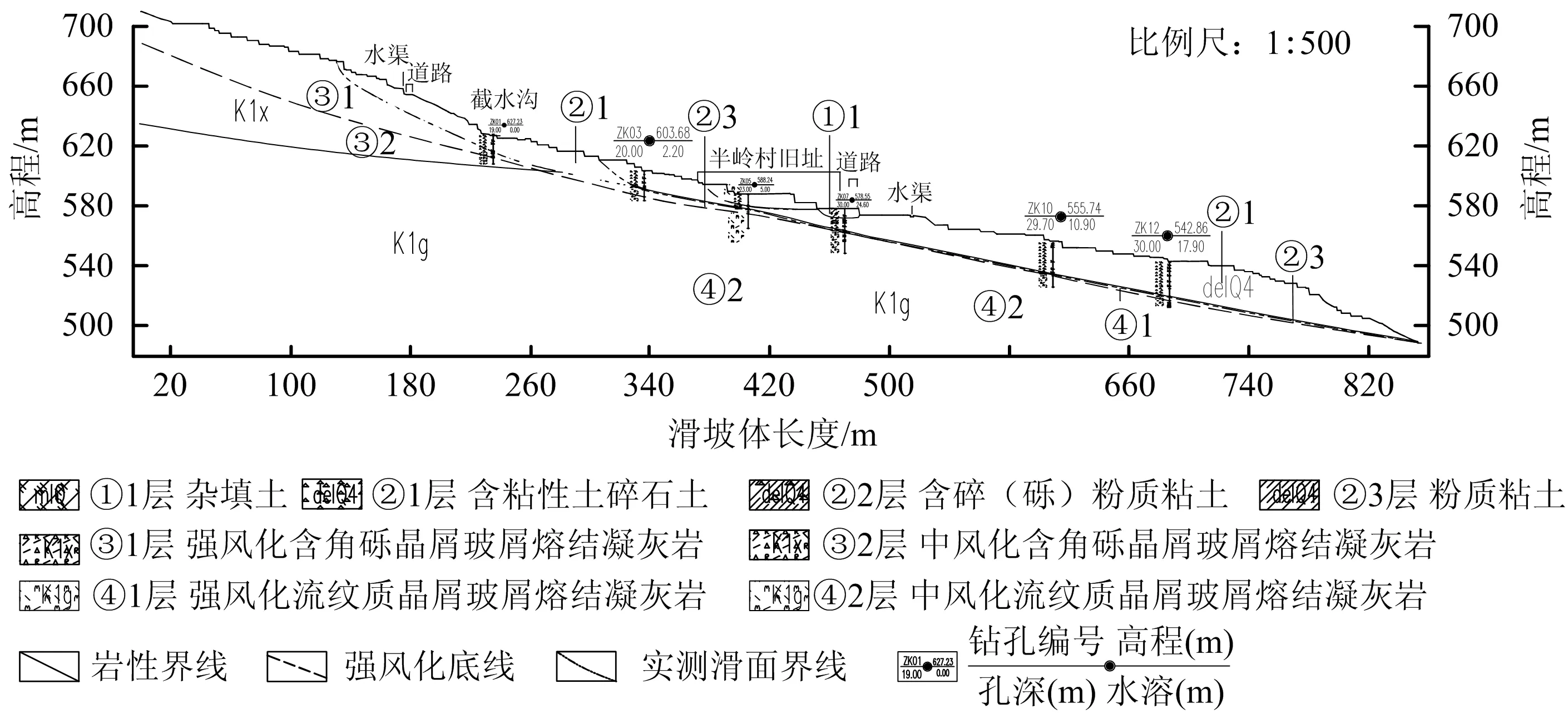
图5 半岭滑坡地质剖面Fig.5 Geological profile of Banling landside

当c和φ值取饱和状态均值时，选择场变量FV1(强度折减系数)和x方向的位移U1作为输出变量，由图6可见，以位移拐点作为边坡稳定的评价标准，安全系数为0.81；若以数值计算不收敛作为评价标准，对应的FV1为0.83。2个数值与极限平衡法算出的FS=0.82以及传递系数法计算的FS=0.81相比都比较接近，如图7所示，说明本方法可行且计算效率高。

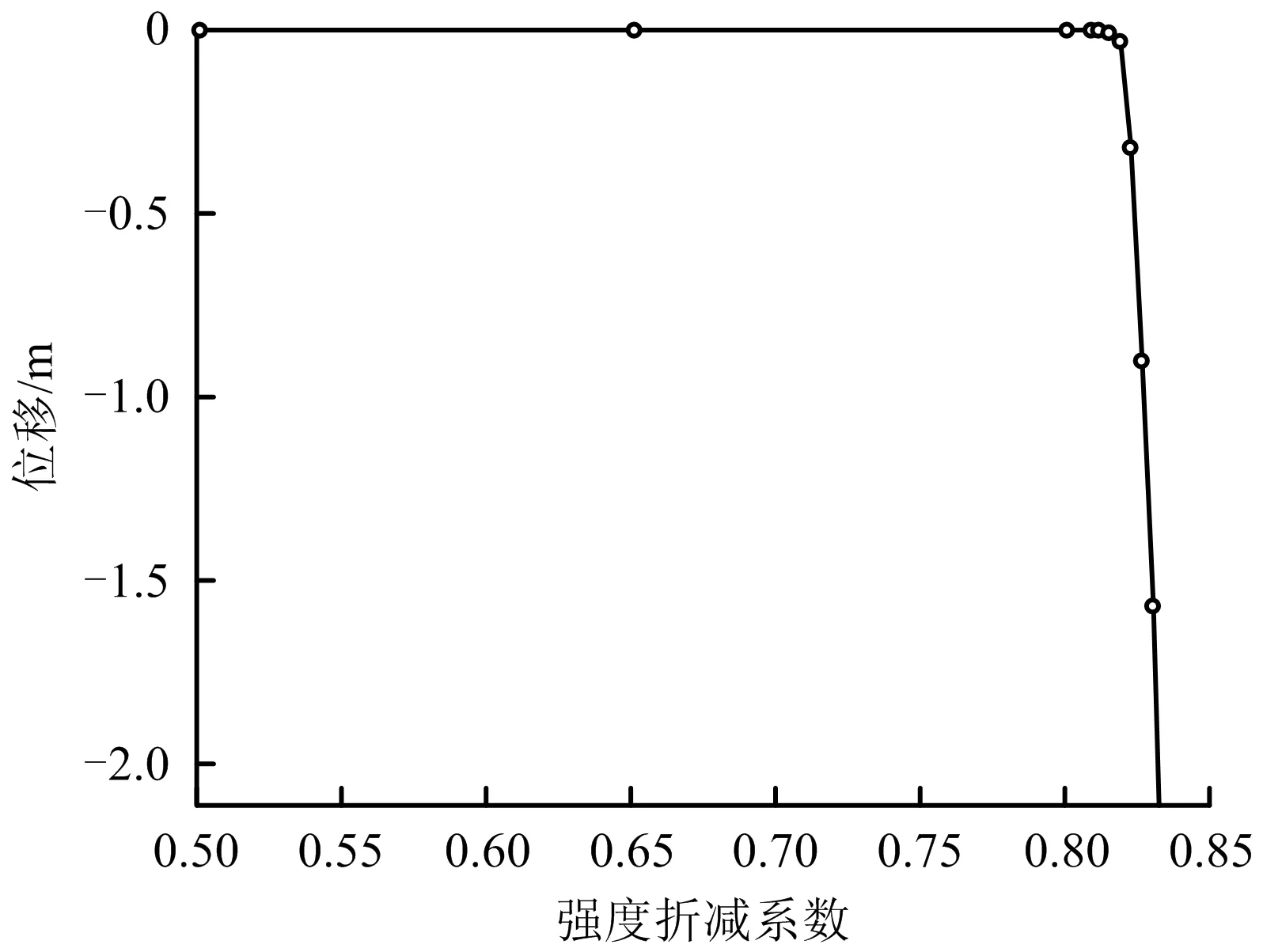
图6 FV1随U1的变化关系Fig.6 Variation relationship of FV1 with U1

图7 传递系数法计算安全系数结果Fig.7 Calculation results of safety coefficient by transfer coefficient method

经过多次计算并结合《滑坡防治工程勘察规范》(DZ/T 0218-2016)表2可知，天然状态下FS为 1.14 左右，基本稳定，与现场勘察时地表裂缝现象是一致的；实验过程中首先从边坡的前缘发生塑性应变，在饱和状态下FS为0.82左右，处于不稳定状态，与勘察期间连续降雨后坡面出现裂缝是一致的，说明滑坡体内地下水丰富且降雨对地下水具有一定的影响，稳定系数下降，若持续强降雨将可能出现滑坡。

根据丽水市勘察测绘院监测结果显示，2017年1月—2017年4月，最大位移量为60 mm,最大变化速率值为10～15 mm/d,边坡达到较危险值，且在连续强降雨期间边坡前缘发生小范围的崩塌。该滑坡的主要成因机制是粉质黏土层长期受地下水浸泡，软化，在滑坡堆积体的自重影响下沿该层发生蠕动。

表2 滑坡稳定状态划分等级Table 2 Grade division of landslide stability state

本次实验选取2个边坡基本物理参数c值φ值，将土工实验得到的天然、饱和数据总共48组参数分别通过ABAQUS软件逐对进行求解安全系数，将数据按比例7∶3划分后作为网络模型训练和检验的样本，如表3～4。

3.2 训练结果分析

经过多次的计算，取粒子群的规模为20，粒子维数12，最大迭代次数250次，初始权重为0.9，c1=c2=1.49，当网络隐含节点数为10左右时，网络的预测性能最好，决定系数均在99%以上，仿真的误差最大不超过0.001；而直接使用RBF网络预测的决定系数在90%左右，精度明显低于PSO-RBF预测的结果,结果如图8所示。由此可见PSO优化后的RBF神经网络适合于本文的研究，RBF拟合出的响应面函数S=f(c,φ)如图9所示。

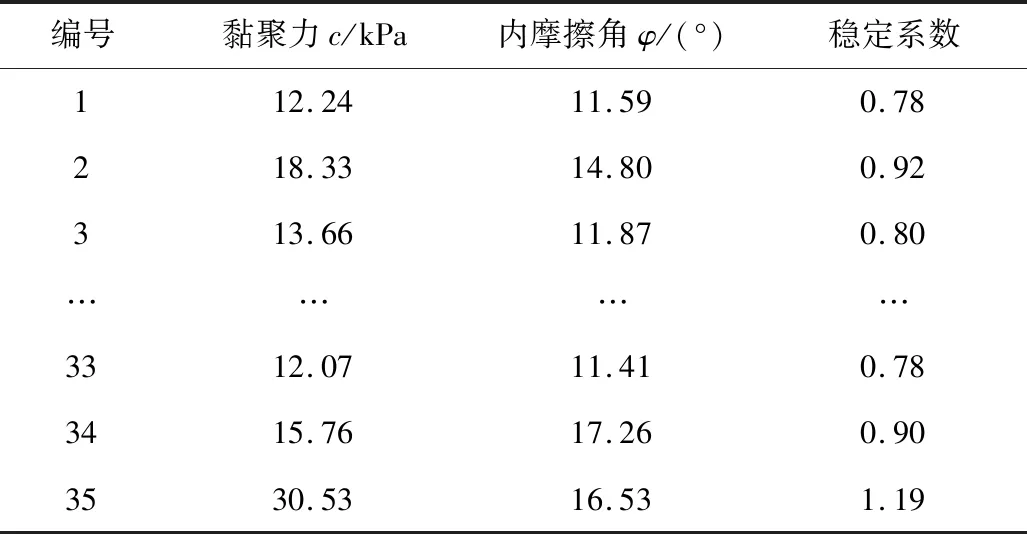
表3 PSO-RBF网络训练样本Table 3 Training samples of PSO-RBF network

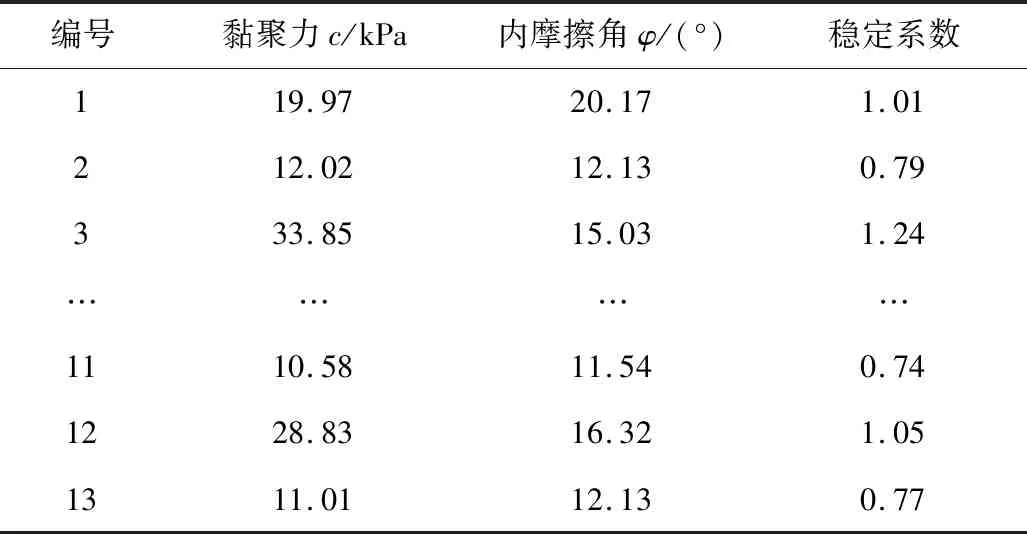
表4 PSO-RBF网络检验样本Table 4 Testing samples of PSO-RBF network

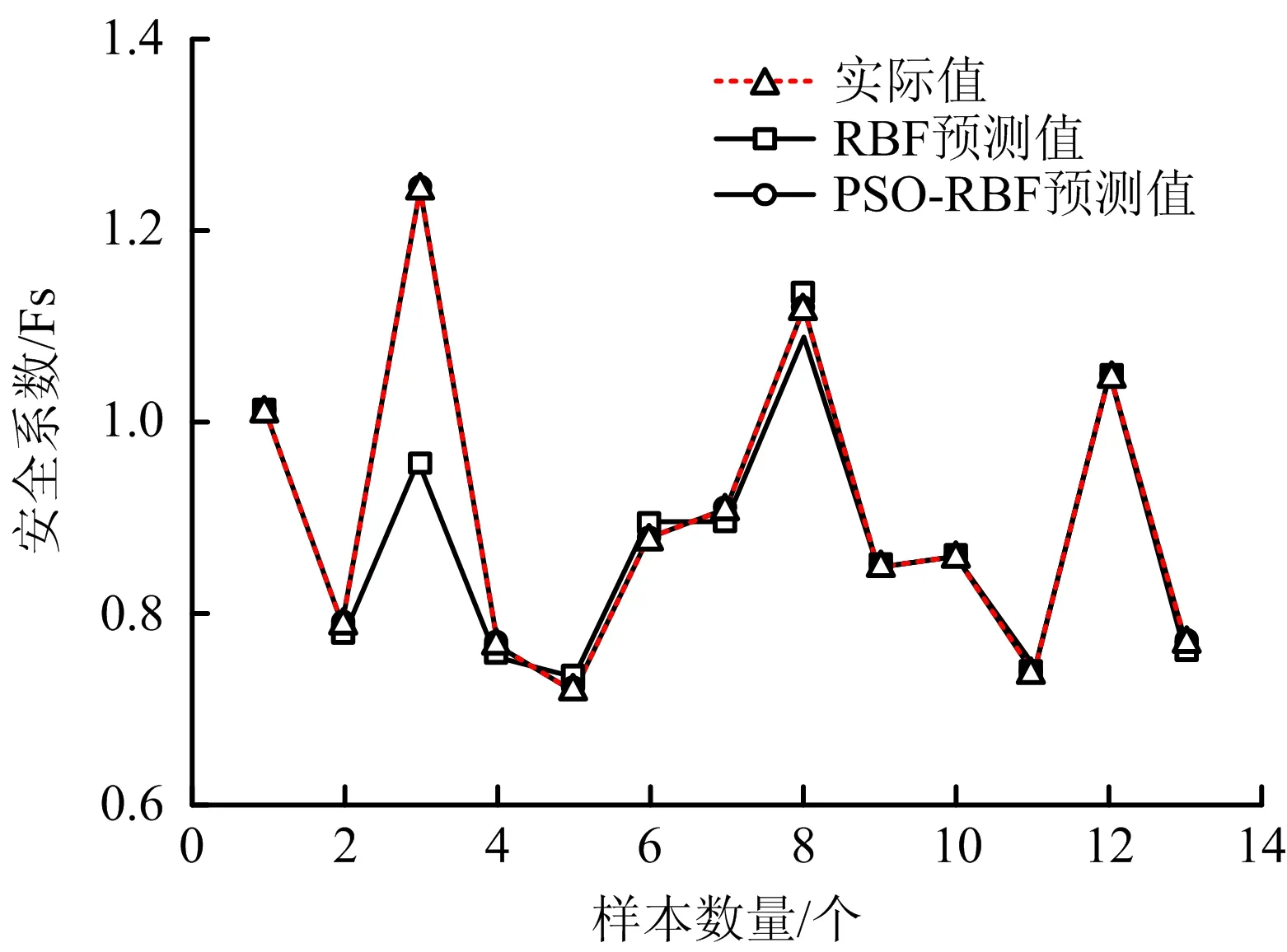
图8 PSO-RBF预测结果Fig.8 PSO-RBF prediction results

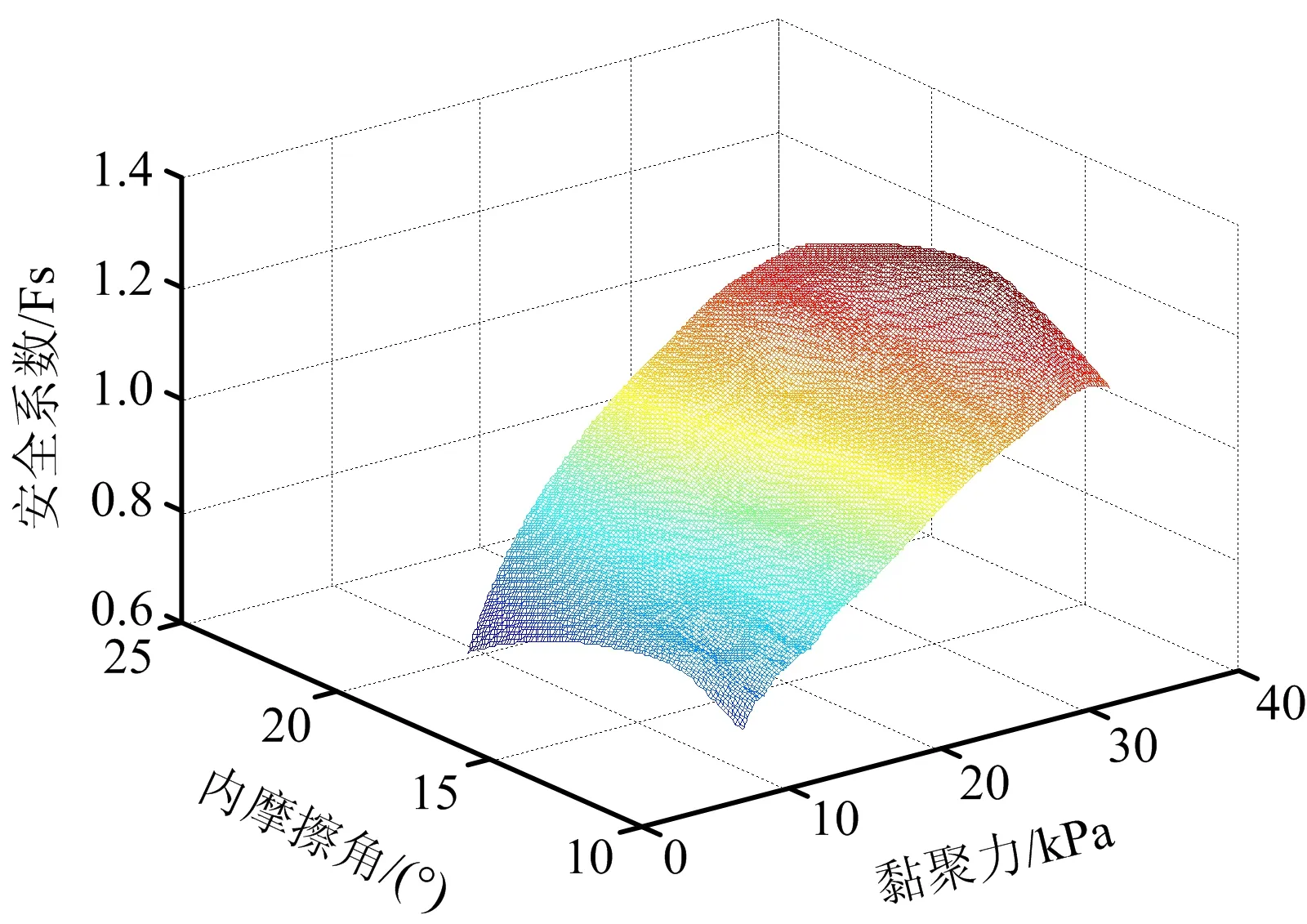
图9 RBF拟合出功能函数曲面Fig.9 Performance function surface fitted by RBF

3.3 蒙特卡罗模拟计算

随机变量通常服从的正分布是非标准正态分布N(0,σ2)，可采用标准正态分布N(0,1)的随机变量x′经过线性转换[13]得到：

X=μ+σx′

(17)

用二元函数变换可得到：

(18)

(19)

式中：X1和X2是标准的正态分布随机变量，u1和u2为[0,1]区间均匀随机数。

随机变量X服从对数正态分布[14]可通过公式Y=lnX转换，则Y服从正态分布。

根据文献[15]可知物理参数的概率分布特性和变异系数相关，得到天然和饱和的黏聚力均服从对数正态分布；同理，2种工况的内摩擦角均服从正态分布，通过对参数值的处理后，利用matlab自带函数随机获取15 000组数据所得c和φ值概率密度分布如图10所示。

图10 c和φ值概率密度分布Fig.10 Distribution of probability densities of and values

将生成的15 000组数据带入训练好的模型中，依次可求得相应的安全系数,则根据公式(12)～(16)得到失稳概率和可靠度指标,见表5。

表5 蒙特卡罗法计算结果Table 5 Calculation results of Monte Carlo

模拟过程中尝试了多次模拟计算，从小到大依次增加模拟次数，当模拟次数2 000以内时，失稳概率值并不稳定，波动比较大，但当模拟的次数超过6 000次后失稳概率值逐渐趋于平稳，最终模拟15 000次达到平稳状态，模拟次数统计见图11。

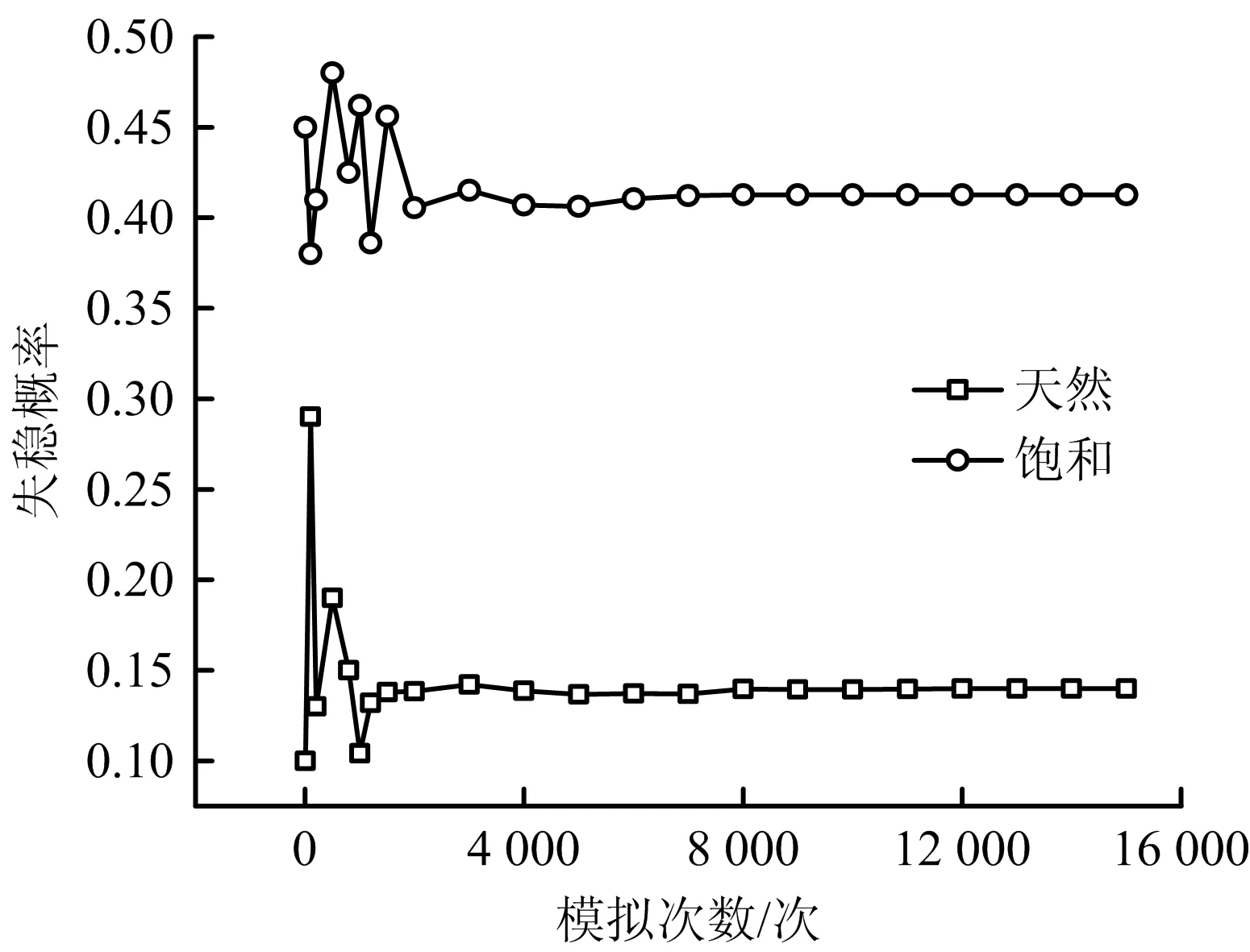
图11 失稳概率随模拟次数的变化Fig.11 Variation of instability probability with number of simulation

3.4 不同方法对比分析

通过计算可以得到边坡天然和饱和2种工况的失稳概率和可靠度指标，再利用文献[5，16]中提到的基于BP网络的可靠度分析法和直接Monte Carlo法得出2种工况边坡的失稳概率和可靠度，计算结果见表6。以直接Monte Carlo法计算结果作为对比对象，基于BP网络可靠度分析法的误差为5.77%和9.52%；基于RBF网络可靠度分析法的误差为2.33%和7.36%；基于PSO-RBF网络可靠度分析方法的误差为0.79%和2.59%。综上所述，本文的方法计算结果误差较小，证明了该方法的可行性。

表6 计算结果对比Table 6 Comparison of calculation results

4 结论

1)本文从理论分析结合具体的实验，验证了基于ABAQUS和RBF神经网络的边坡可靠度分析方法的可行性。

2)以具体的边坡作为实例，利用土工实验以及野外勘探所得参数和ABAQUS强度折减法计算结果构造样本数据，利用PSO算法对RBF神经网络模型进行优化后拟合出功能函数；再通过Monte Carlo模拟法得到边坡的失稳概率和可靠指标。

3)对于c值和φ值的分布形式做出了合适的判断，训练的样本数据包括了天然和饱和2种状态，使得模型的准确度达到了99%以上，该方法和其他相关方法计算的结果相近，但利用了RBF神经网络训练简单，学习收敛速度快，能够逼近任意非线性函数的优点，构造边坡极限状态响应面，拟合精度好，模型简单直观，计算效率更高；通过PSO优化网络使得计算精度相对于单一的RBF网络法有进一步的提高，引入了可靠度分析方法，避免了传统方法的一些缺点，对日后的滑坡风险评价起到技术支撑作用，在实际工程中具有一定实用价值。